Question Number 38057 by ajfour last updated on 21/Jun/18
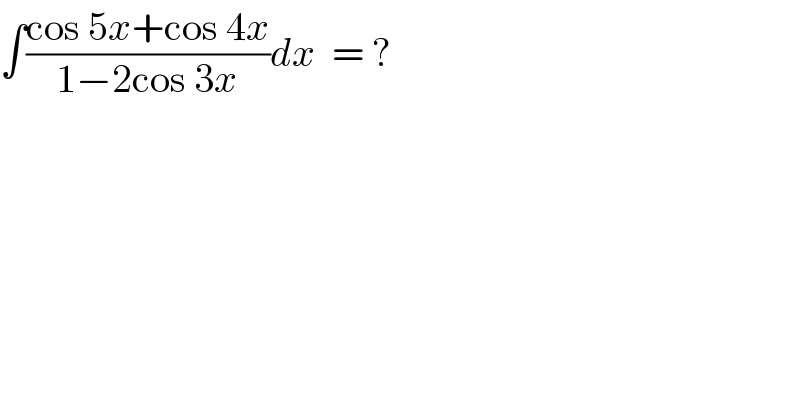
$$\int\frac{\mathrm{cos}\:\mathrm{5}{x}+\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{1}−\mathrm{2cos}\:\mathrm{3}{x}}{dx}\:\:=\:? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jun/18

$$\int\frac{{sin}\mathrm{3}{x}\left({cos}\mathrm{5}{x}+{coz}\mathrm{4}{x}\right)}{{sin}\mathrm{3}{x}−{sin}\mathrm{6}{x}}{dx} \\ $$$$\int\frac{{sin}\mathrm{3}{x}\left({cos}\mathrm{5}{x}+{cos}\mathrm{4}{x}\right)}{−\mathrm{2}{cos}\frac{\mathrm{9}{x}}{\mathrm{2}}{sin}\frac{\mathrm{3}{x}}{\mathrm{2}}}{dx} \\ $$$$\int\frac{\mathrm{2}{sin}\frac{\mathrm{3}{x}}{\mathrm{2}}{cos}\frac{\mathrm{3}{x}}{\mathrm{2}}×\mathrm{2}{cos}\frac{\mathrm{9}{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}}{−\mathrm{2}{cos}\frac{\mathrm{9}{x}}{\mathrm{2}}{sin}\frac{\mathrm{3}{x}}{\mathrm{2}}}{dx} \\ $$$$=−\mathrm{1}×\int\frac{\mathrm{2}{cos}\frac{\mathrm{3}{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}}{}{dx} \\ $$$$=−\mathrm{1}×\int\left({cos}\mathrm{2}{x}+{cosx}\right){dx} \\ $$$$=−\mathrm{1}×\left\{\frac{{sin}\mathrm{2}{x}}{\mathrm{2}}+\frac{{sinx}}{}\right\}+{c} \\ $$
Commented by ajfour last updated on 21/Jun/18
$${Very}\:{quick}\:{and}\:{right}\:{Sir}. \\ $$
