Menu Close

cos-5x-cos-4x-1-2cos-3x-dx-tan-x-sin-2x-dx-dx-cos-3-x-sin-5-x-

Tinku Tara 0 Comments
Pin




Question Number 146597 by iloveisrael last updated on 14/Jul/21
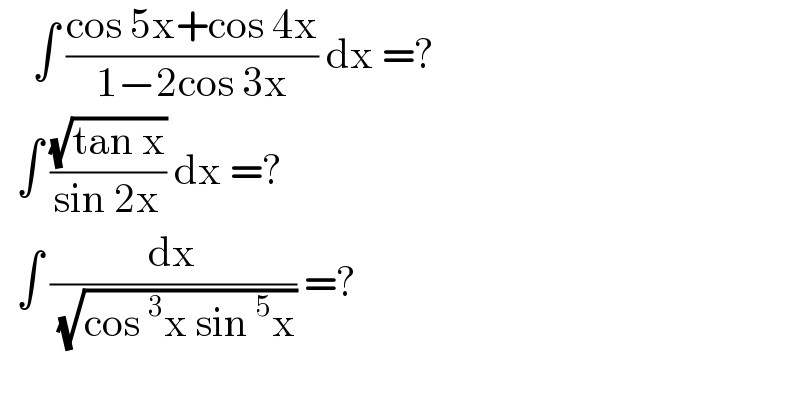
∫ ((cos 5x+cos 4x)/(1−2cos 3x)) dx =? ∫ ((√(tan x))/(sin 2x)) dx =? ∫ (dx/( (√(cos^3 x sin^5 x)))) =?
$$\:\:\:\:\int\:\frac{\mathrm{cos}\:\mathrm{5x}+\mathrm{cos}\:\mathrm{4x}}{\mathrm{1}−\mathrm{2cos}\:\mathrm{3x}}\:\mathrm{dx}\:=?\: \\ $$$$\:\:\int\:\frac{\sqrt{\mathrm{tan}\:\mathrm{x}}}{\mathrm{sin}\:\mathrm{2x}}\:\mathrm{dx}\:=? \\ $$$$\:\:\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}\:\mathrm{sin}\:^{\mathrm{5}} \mathrm{x}}}\:=? \\ $$
Answered by gsk2684 last updated on 14/Jul/21
∫((cos 5x+cos 4x)/(1−2cos 3x))dx ∫ ((2cos ((5x+4x)/2)cos ((5x−4x)/2))/(1−2(2cos^2 ((3x)/2)−1))) dx 2∫((cos 3(((3x)/2))cos (x/2))/(1−4cos^2 ((3x)/2)+2))dx 2∫(([4cos^3 (((3x)/2))−3cos(((3x)/2))] cos (x/2))/(3−4cos^2 ((3x)/2)))dx 2∫(([4cos^2 (((3x)/2))−3]cos ((3x)/2) cos (x/2))/(3−4cos^2 ((3x)/2)))dx −∫2cos ((3x)/2)cos (x/2)dx −∫(cos (((3x)/2)+(x/2))+cos (((3x)/2)−(x/2)))dx −∫(cos 2x+cos x)dx −(((sin 2x)/2)+sin x)+c
$$\int\frac{\mathrm{cos}\:\mathrm{5}{x}+\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{1}−\mathrm{2cos}\:\mathrm{3}{x}}{dx} \\ $$$$\int\:\frac{\mathrm{2cos}\:\frac{\mathrm{5}{x}+\mathrm{4}{x}}{\mathrm{2}}\mathrm{cos}\:\frac{\mathrm{5}{x}−\mathrm{4}{x}}{\mathrm{2}}}{\mathrm{1}−\mathrm{2}\left(\mathrm{2cos}\:^{\mathrm{2}} \frac{\mathrm{3}{x}}{\mathrm{2}}−\mathrm{1}\right)}\:{dx} \\ $$$$\mathrm{2}\int\frac{\mathrm{cos}\:\mathrm{3}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\frac{{x}}{\mathrm{2}}}{\mathrm{1}−\mathrm{4cos}\:^{\mathrm{2}} \frac{\mathrm{3}{x}}{\mathrm{2}}+\mathrm{2}}{dx} \\ $$$$\mathrm{2}\int\frac{\left[\mathrm{4cos}\:^{\mathrm{3}} \left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)−\mathrm{3cos}\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\right]\:\mathrm{cos}\:\frac{{x}}{\mathrm{2}}}{\mathrm{3}−\mathrm{4cos}\:^{\mathrm{2}} \frac{\mathrm{3}{x}}{\mathrm{2}}}{dx} \\ $$$$\mathrm{2}\int\frac{\left[\mathrm{4cos}\:^{\mathrm{2}} \left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)−\mathrm{3}\right]\mathrm{cos}\:\frac{\mathrm{3}{x}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{x}}{\mathrm{2}}}{\mathrm{3}−\mathrm{4cos}\:^{\mathrm{2}} \frac{\mathrm{3}{x}}{\mathrm{2}}}{dx} \\ $$$$−\int\mathrm{2cos}\:\frac{\mathrm{3}{x}}{\mathrm{2}}\mathrm{cos}\:\frac{{x}}{\mathrm{2}}{dx} \\ $$$$−\int\left(\mathrm{cos}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}+\frac{{x}}{\mathrm{2}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\right)\right){dx} \\ $$$$−\int\left(\mathrm{cos}\:\mathrm{2}{x}+\mathrm{cos}\:{x}\right){dx} \\ $$$$−\left(\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}}+\mathrm{sin}\:{x}\right)+{c} \\ $$
Answered by gsk2684 last updated on 14/Jul/21
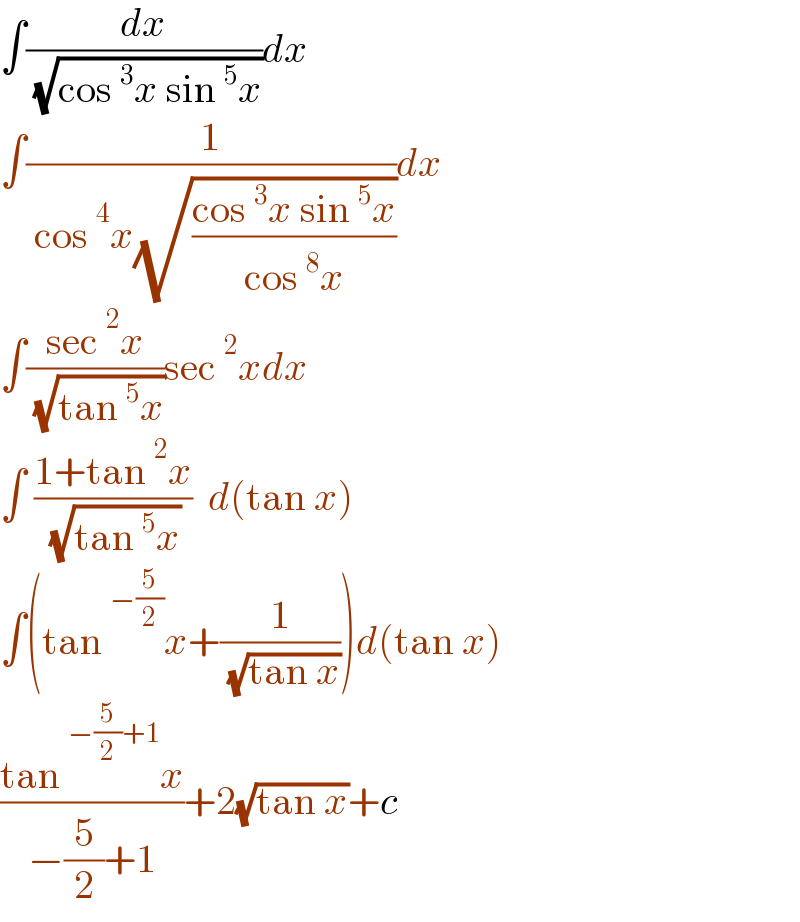
∫(dx/( (√(cos^3 x sin^5 x))))dx ∫(1/( cos^4 x(√((cos^3 x sin^5 x)/(cos^8 x)))))dx ∫((sec^2 x)/( (√(tan^5 x))))sec^2 xdx ∫ ((1+tan^2 x)/( (√(tan^5 x)))) d(tan x) ∫(tan^(−(5/2)) x+(1/( (√(tan x)))))d(tan x) ((tan^(−(5/2)+1) x)/(−(5/2)+1))+2(√(tan x))+c
$$\int\frac{{dx}}{\:\sqrt{\mathrm{cos}\:^{\mathrm{3}} {x}\:\mathrm{sin}\:^{\mathrm{5}} {x}}}{dx} \\ $$$$\int\frac{\mathrm{1}}{\:\mathrm{cos}\:^{\mathrm{4}} {x}\sqrt{\frac{\mathrm{cos}\:^{\mathrm{3}} {x}\:\mathrm{sin}\:^{\mathrm{5}} {x}}{\mathrm{cos}\:^{\mathrm{8}} {x}}}}{dx} \\ $$$$\int\frac{\mathrm{sec}\:^{\mathrm{2}} {x}}{\:\sqrt{\mathrm{tan}\:^{\mathrm{5}} {x}}}\mathrm{sec}\:^{\mathrm{2}} {xdx} \\ $$$$\int\:\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}}{\:\sqrt{\mathrm{tan}\:^{\mathrm{5}} {x}}}\:\:{d}\left(\mathrm{tan}\:{x}\right) \\ $$$$\int\left(\mathrm{tan}\:^{−\frac{\mathrm{5}}{\mathrm{2}}} {x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\:{x}}}\right){d}\left(\mathrm{tan}\:{x}\right) \\ $$$$\frac{\mathrm{tan}\:^{−\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{1}} {x}}{−\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{1}}+\mathrm{2}\sqrt{\mathrm{tan}\:{x}}+{c} \\ $$
Answered by gsk2684 last updated on 14/Jul/21
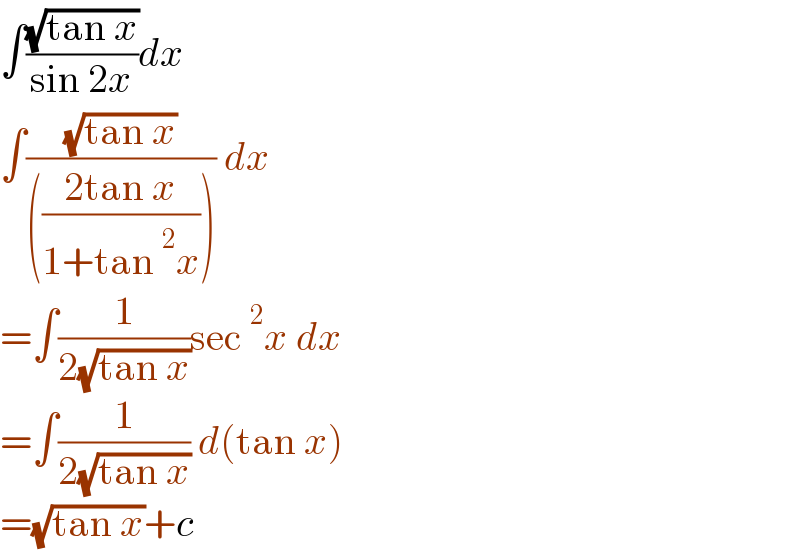
∫((√(tan x))/(sin 2x))dx ∫((√(tan x))/((((2tan x)/(1+tan^2 x))))) dx =∫(1/(2(√(tan x))))sec^2 x dx =∫(1/(2(√(tan x)))) d(tan x) =(√(tan x))+c
$$\int\frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{sin}\:\mathrm{2}{x}}{dx} \\ $$$$\int\frac{\sqrt{\mathrm{tan}\:{x}}}{\left(\frac{\mathrm{2tan}\:{x}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}}\right)}\:{dx} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{tan}\:{x}}}\mathrm{sec}\:^{\mathrm{2}} {x}\:{dx} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{tan}\:{x}}}\:{d}\left(\mathrm{tan}\:{x}\right) \\ $$$$=\sqrt{\mathrm{tan}\:{x}}+{c} \\ $$
Answered by puissant last updated on 14/Jul/21
2) ∫((√(tan x))/(sin 2x))dx=K u=(√(tan x ))⇒u^2 =tan x 2udu=(dx/(cos^2 x)) ⇒ dx=2ucos^2 x dx K=∫(u/(2sin x cos x))×2ucos^2 x du =∫(u^2 /(tan x))du=∫(u^2 /u^2 )du= u+c ⇒K=(√(tan x))+c..
$$\left.\mathrm{2}\right) \\ $$$$\int\frac{\sqrt{\mathrm{tan}\:\mathrm{x}}}{\mathrm{sin}\:\mathrm{2x}}\mathrm{dx}=\mathrm{K} \\ $$$$\mathrm{u}=\sqrt{\mathrm{tan}\:\mathrm{x}\:}\Rightarrow\mathrm{u}^{\mathrm{2}} =\mathrm{tan}\:\mathrm{x}\:\:\:\mathrm{2udu}=\frac{\mathrm{dx}}{\mathrm{cos}^{\mathrm{2}} \:\mathrm{x}} \\ $$$$\Rightarrow\:\mathrm{dx}=\mathrm{2ucos}^{\mathrm{2}} \:\mathrm{x}\:\mathrm{dx} \\ $$$$\mathrm{K}=\int\frac{\mathrm{u}}{\mathrm{2sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}×\mathrm{2ucos}^{\mathrm{2}} \:\mathrm{x}\:\mathrm{du} \\ $$$$=\int\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{tan}\:\mathrm{x}}\mathrm{du}=\int\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{2}} }\mathrm{du}=\:\mathrm{u}+\mathrm{c} \\ $$$$\Rightarrow\mathrm{K}=\sqrt{\mathrm{tan}\:\mathrm{x}}+\mathrm{c}.. \\ $$
Answered by mathmax by abdo last updated on 14/Jul/21
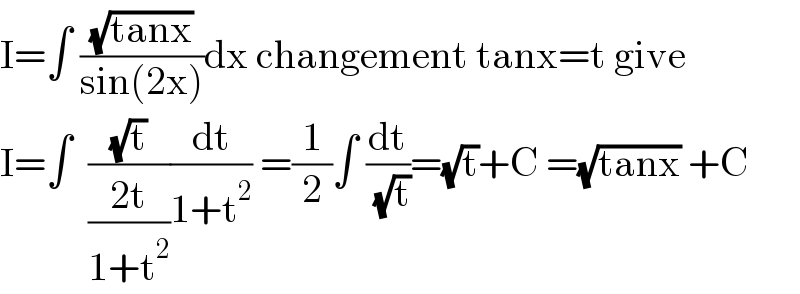
I=∫ ((√(tanx))/(sin(2x)))dx changement tanx=t give I=∫ ((√t)/((2t)/(1+t^2 )))(dt/(1+t^2 )) =(1/2)∫ (dt/( (√t)))=(√t)+C =(√(tanx)) +C
$$\mathrm{I}=\int\:\frac{\sqrt{\mathrm{tanx}}}{\mathrm{sin}\left(\mathrm{2x}\right)}\mathrm{dx}\:\mathrm{changement}\:\mathrm{tanx}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}=\int\:\:\frac{\sqrt{\mathrm{t}}}{\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{t}}}=\sqrt{\mathrm{t}}+\mathrm{C}\:=\sqrt{\mathrm{tanx}}\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *