Question Number 82604 by jagoll last updated on 23/Feb/20
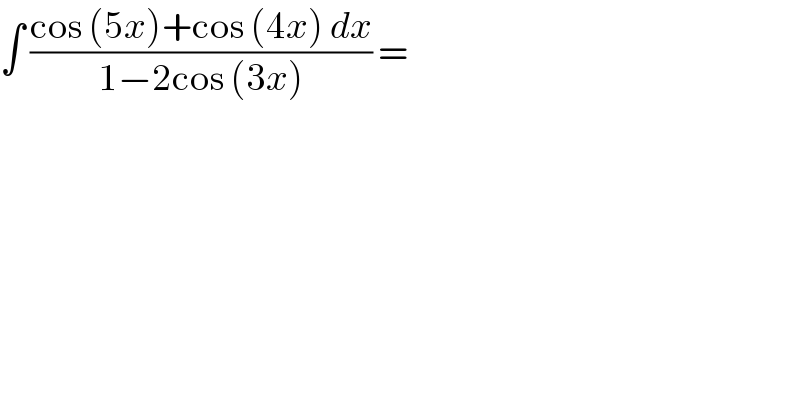
$$\int\:\frac{\mathrm{cos}\:\left(\mathrm{5}{x}\right)+\mathrm{cos}\:\left(\mathrm{4}{x}\right)\:{dx}}{\mathrm{1}−\mathrm{2cos}\:\left(\mathrm{3}{x}\right)}\:=\: \\ $$
Answered by john santu last updated on 23/Feb/20

$$\int\:\:\frac{\left\{\mathrm{cos}\:\left(\mathrm{5}{x}\right)+\mathrm{cos}\:\left(\mathrm{4}{x}\right)\right\}\mathrm{sin}\:\left(\mathrm{3}{x}\right)}{\mathrm{sin}\:\left(\mathrm{3}{x}\right)−\mathrm{sin}\:\left(\mathrm{6}{x}\right)}\:{dx} \\ $$$$=\mathrm{2}\int\:\frac{\left\{\mathrm{cos}\:\left(\frac{\mathrm{9}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}}{\mathrm{2}}\right)\right\}\mathrm{sin}\:\left(\mathrm{3}{x}\right)}{\mathrm{2cos}\:\left(\frac{\mathrm{9}{x}}{\mathrm{2}}\right)\mathrm{sin}\:\left(−\frac{\mathrm{3}{x}}{\mathrm{2}}\right)}\:{dx} \\ $$$$=\:−\:\int\:\frac{\mathrm{sin}\:\left(\mathrm{3}{x}\right)\mathrm{cos}\:\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{sin}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)}\:{dx}\: \\ $$$$=\:−\int\:\frac{\mathrm{2sin}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{sin}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)}\:{dx}\: \\ $$$$=\:−\int\:\mathrm{2cos}\:\left(\frac{\mathrm{3}{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}}{\mathrm{2}}\right)\:{dx}\: \\ $$$$=\:−\:\int\:\left\{\mathrm{cos}\:\mathrm{2}{x}\:+\:\mathrm{cos}\:{x}\right\}\:{dx}\: \\ $$$$=\:−\left\{\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{x}−\mathrm{sin}\:{x}\:\right\}\:+\:{c} \\ $$$$=\:−\mathrm{sin}\:{x}\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\:+\:{c} \\ $$$$=\:\mathrm{sin}\:{x}\:\left(\mathrm{1}−\mathrm{cos}\:{x}\right)\:+\:{c}\: \\ $$
Commented by jagoll last updated on 23/Feb/20

$${thank}\:{you}\:{sir} \\ $$
Commented by peter frank last updated on 23/Feb/20

$${thank}\:{you} \\ $$
