cos-cos-sin-sin-sin-sin-cos-cos-prove-ghis-

Question Number 35951 by gyugfeet last updated on 26/May/18

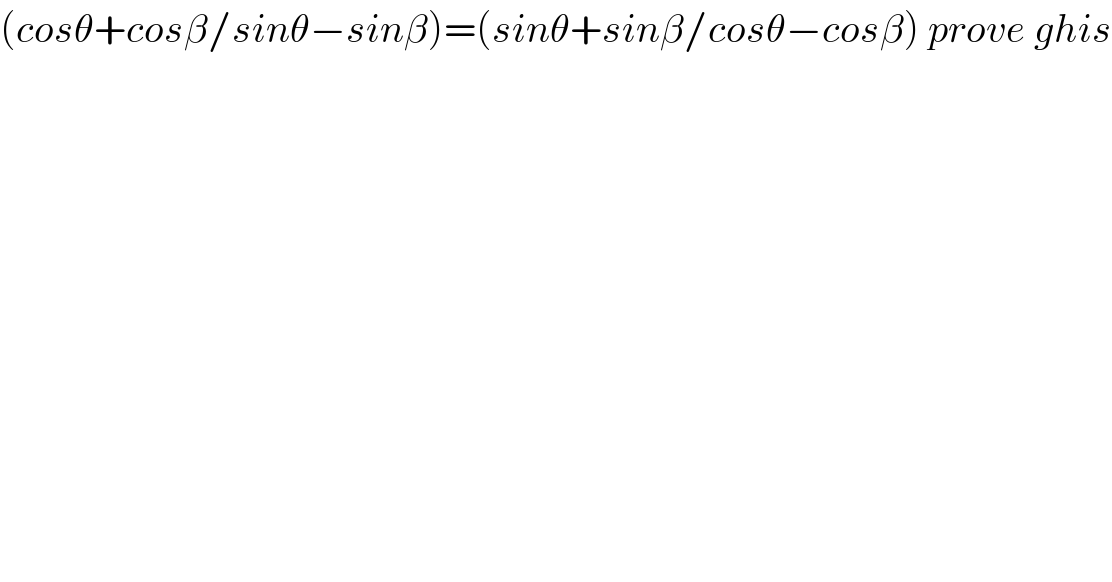
(cosθ+cosβ/sinθ−sinβ)=(sinθ+sinβ/cosθ−cosβ) prove ghis

$$\left({cos}\theta+{cos}\beta/{sin}\theta−{sin}\beta\right)=\left({sin}\theta+{sin}\beta/{cos}\theta−{cos}\beta\right)\:{prove}\:{ghis} \\ $$

Commented by Rasheed.Sindhi last updated on 27/May/18

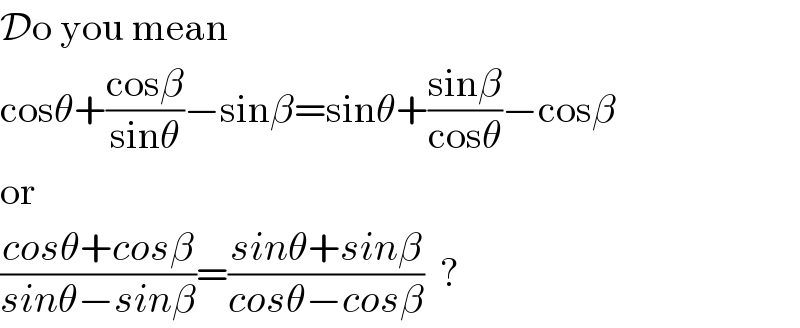
Do you mean cosθ+((cosβ)/(sinθ))−sinβ=sinθ+((sinβ)/(cosθ))−cosβ or ((cosθ+cosβ)/(sinθ−sinβ))=((sinθ+sinβ)/(cosθ−cosβ)) ?

$$\mathcal{D}\mathrm{o}\:\mathrm{you}\:\mathrm{mean} \\ $$$$\mathrm{cos}\theta+\frac{\mathrm{cos}\beta}{\mathrm{sin}\theta}−\mathrm{sin}\beta=\mathrm{sin}\theta+\frac{\mathrm{sin}\beta}{\mathrm{cos}\theta}−\mathrm{cos}\beta \\ $$$$\mathrm{or} \\ $$$$\frac{{cos}\theta+{cos}\beta}{{sin}\theta−{sin}\beta}=\frac{{sin}\theta+{sin}\beta}{{cos}\theta−{cos}\beta}\:\:? \\ $$

Commented by gyugfeet last updated on 27/May/18

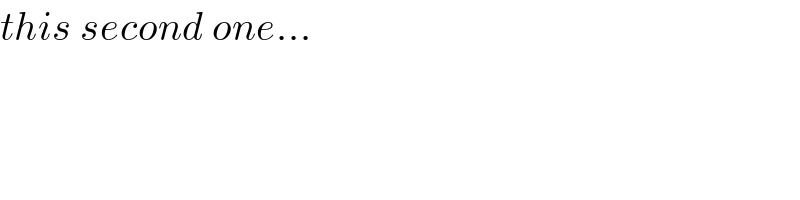
$${this}\:{second}\:{one}… \\ $$

Commented by Rasheed.Sindhi last updated on 28/May/18

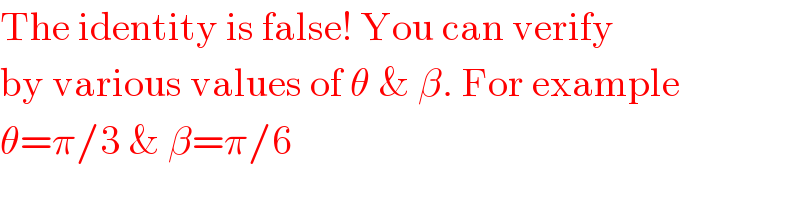
The identity is false! You can verify by various values of θ & β. For example θ=π/3 & β=π/6

$$\mathrm{The}\:\mathrm{identity}\:\mathrm{is}\:\mathrm{false}!\:\mathrm{You}\:\mathrm{can}\:\mathrm{verify} \\ $$$$\mathrm{by}\:\mathrm{various}\:\mathrm{values}\:\mathrm{of}\:\theta\:\&\:\beta.\:\mathrm{For}\:\mathrm{example} \\ $$$$\theta=\pi/\mathrm{3}\:\&\:\beta=\pi/\mathrm{6} \\ $$

Answered by Rasheed.Sindhi last updated on 28/May/18

((cosθ+cosβ)/(sinθ−sinβ))=((sinθ+sinβ)/(cosθ−cosβ)) LHS ((cosθ+cosβ)/(sinθ−sinβ)) =((2cos(((a+b)/2))cos(((a+b)/2)) )/(2cos(((a+b)/2))sin(((a−b)/2)) ))=((cos(((a+b)/2)) )/(sin(((a−b)/2)) )) RHS ((sinθ+sinβ)/(cosθ−cosβ))=((2sin(((a+b)/2))cos(((a−b)/2)) )/(−2sin(((a+b)/2))sin(((a−b)/2)) )) =−((cos(((a−b)/2)) )/(sin(((a−b)/2)) ))=−tan(((a−b)/2)) ???

$$\frac{{cos}\theta+{cos}\beta}{{sin}\theta−{sin}\beta}=\frac{{sin}\theta+{sin}\beta}{{cos}\theta−{cos}\beta} \\ $$$$\mathrm{LHS} \\ $$$$\frac{{cos}\theta+{cos}\beta}{{sin}\theta−{sin}\beta} \\ $$$$=\frac{\mathrm{2cos}\left(\frac{{a}+{b}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{{a}+{b}}{\mathrm{2}}\right)\:\:}{\mathrm{2cos}\left(\frac{{a}+{b}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{{a}−{b}}{\mathrm{2}}\right)\:\:}=\frac{\mathrm{cos}\left(\frac{{a}+{b}}{\mathrm{2}}\right)\:\:}{\mathrm{sin}\left(\frac{{a}−{b}}{\mathrm{2}}\right)\:\:} \\ $$$$\mathrm{RHS} \\ $$$$\frac{{sin}\theta+{sin}\beta}{{cos}\theta−{cos}\beta}=\frac{\mathrm{2sin}\left(\frac{{a}+{b}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right)\:\:}{−\mathrm{2sin}\left(\frac{{a}+{b}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{{a}−{b}}{\mathrm{2}}\right)\:\:} \\ $$$$=−\frac{\mathrm{cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right)\:\:}{\mathrm{sin}\left(\frac{{a}−{b}}{\mathrm{2}}\right)\:\:}=−\mathrm{tan}\left(\frac{{a}−{b}}{\mathrm{2}}\right)\: \\ $$$$\:\:\:\:\:\:\:\:??? \\ $$

Facebook Tweet Pin

cos-cos-sin-sin-sin-sin-cos-cos-prove-ghis-

Leave a Reply Cancel reply