Menu Close

cos-n-x-dx-please-i-need-workings-

Tinku Tara 0 Comments
Pin




Question Number 14014 by tawa tawa last updated on 26/May/17
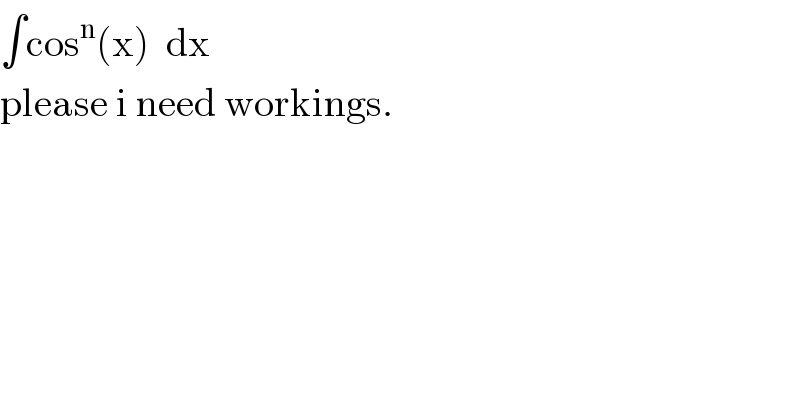
∫cos^n (x) dx please i need workings.
$$\int\mathrm{cos}^{\mathrm{n}} \left(\mathrm{x}\right)\:\:\mathrm{dx} \\ $$$$\mathrm{please}\:\mathrm{i}\:\mathrm{need}\:\mathrm{workings}. \\ $$
Answered by mrW1 last updated on 26/May/17
I_n =∫cos^n (x) dx=∫cos^(n−1) (x) dsin (x) using ∫udv=uv−∫vdu =sin (x) cos^(n−1) (x)+(n−1)∫sin^2 (x) cos^(n−2) (x)dx =sin (x) cos^(n−1) (x)+(n−1)∫[1−cos^2 (x)] cos^(n−2) (x)dx =sin (x) cos^(n−1) (x)+(n−1)∫cos^(n−2) (x) dx−(n−1)∫cos^n (x) dx ⇒I_n =sin (x) cos^(n−1) (x)+(n−1)∫cos^(n−2) (x) dx−(n−1)I_n ⇒nI_n =sin (x) cos^(n−1) (x)+(n−1)I_(n−2) ⇒I_n =(1/n)sin (x) cos^(n−1) (x)+((n−1)/n)I_(n−2) ⇒I_(n−2) =(1/(n−2))sin (x) cos^(n−3) (x)+((n−3)/(n−2))I_(n−4) ...... if n=even .... ⇒I_2 =(1/2)sin (x) cos (x)+(1/2)I_0 ⇒I_0 =∫dx=x+C ...... if n=odd .... ⇒I_3 =(1/3)sin (x) cos^2 (x)+(2/3)I_1 ⇒I_1 =∫cos (x) dx=sin (x)+C
$${I}_{{n}} =\int\mathrm{cos}^{\mathrm{n}} \left(\mathrm{x}\right)\:\:\mathrm{dx}=\int\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)\:{d}\mathrm{sin}\:\left({x}\right) \\ $$$${using}\:\int{udv}={uv}−\int{vdu} \\ $$$$=\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\left({n}−\mathrm{1}\right)\int\mathrm{sin}^{\mathrm{2}} \:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{2}} \:\left({x}\right){dx} \\ $$$$=\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\left({n}−\mathrm{1}\right)\int\left[\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\left({x}\right)\right]\:\mathrm{cos}^{{n}−\mathrm{2}} \:\left({x}\right){dx} \\ $$$$=\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\left({n}−\mathrm{1}\right)\int\mathrm{cos}^{{n}−\mathrm{2}} \:\left({x}\right)\:{dx}−\left({n}−\mathrm{1}\right)\int\mathrm{cos}^{{n}} \:\left({x}\right)\:{dx} \\ $$$$\Rightarrow{I}_{{n}} =\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\left({n}−\mathrm{1}\right)\int\mathrm{cos}^{{n}−\mathrm{2}} \:\left({x}\right)\:{dx}−\left({n}−\mathrm{1}\right){I}_{{n}} \\ $$$$\Rightarrow{nI}_{{n}} =\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\left({n}−\mathrm{1}\right){I}_{{n}−\mathrm{2}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{1}}{{n}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\frac{{n}−\mathrm{1}}{{n}}{I}_{{n}−\mathrm{2}} \\ $$$$\Rightarrow{I}_{{n}−\mathrm{2}} =\frac{\mathrm{1}}{{n}−\mathrm{2}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{3}} \:\left({x}\right)+\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}{I}_{{n}−\mathrm{4}} \\ $$$$……\:{if}\:{n}={even}\:…. \\ $$$$\Rightarrow{I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}\:\left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{0}} \\ $$$$\Rightarrow{I}_{\mathrm{0}} =\int{dx}={x}+{C} \\ $$$$ \\ $$$$……\:{if}\:{n}={odd}\:…. \\ $$$$\Rightarrow{I}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{\mathrm{2}} \:\left({x}\right)+\frac{\mathrm{2}}{\mathrm{3}}{I}_{\mathrm{1}} \\ $$$$\Rightarrow{I}_{\mathrm{1}} =\int\mathrm{cos}\:\left({x}\right)\:{dx}=\mathrm{sin}\:\left({x}\right)+{C} \\ $$
Commented by tawa tawa last updated on 26/May/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mrW1 last updated on 27/May/17
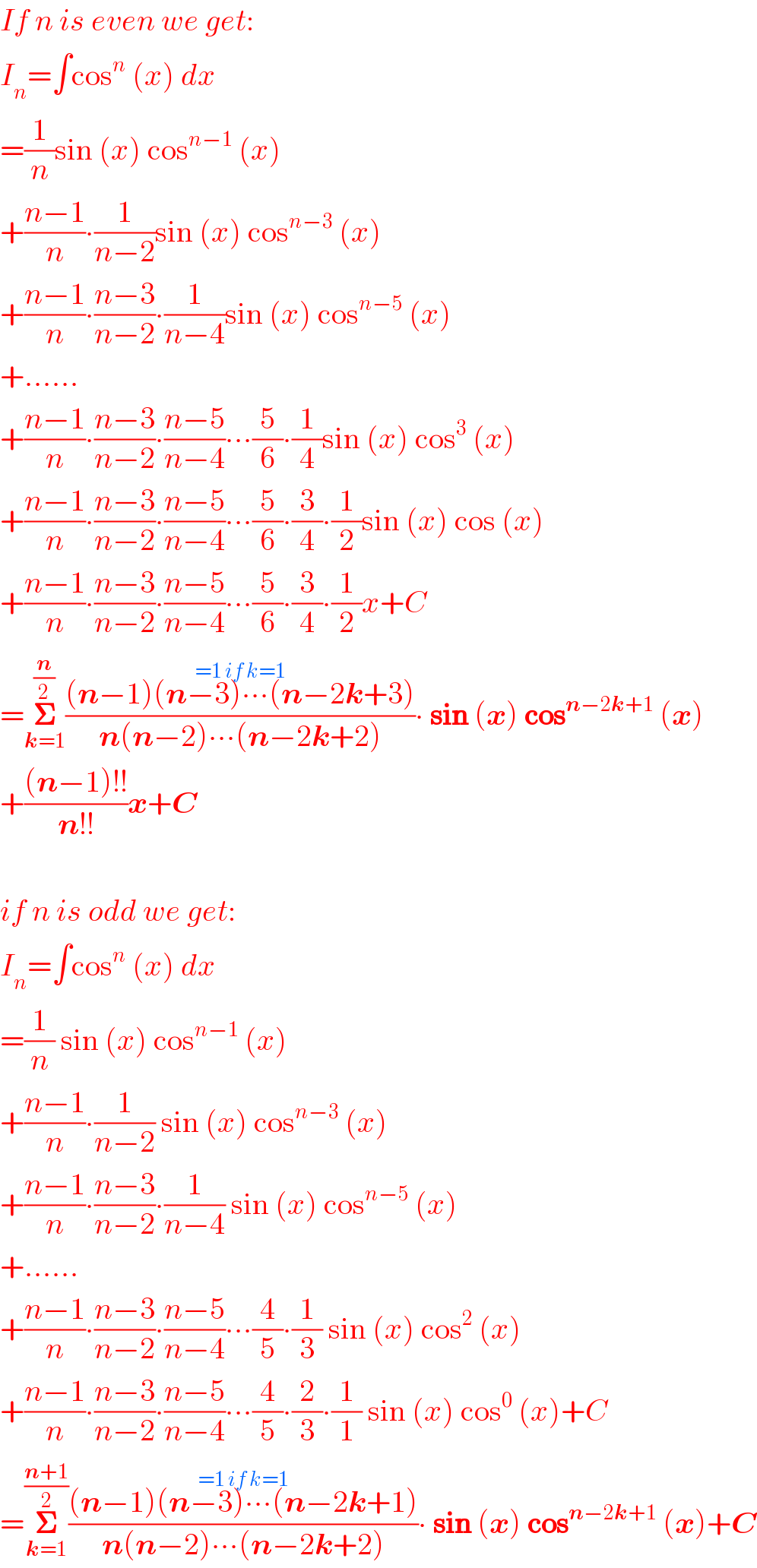
If n is even we get: I_n =∫cos^n (x) dx =(1/n)sin (x) cos^(n−1) (x) +((n−1)/n)∙(1/(n−2))sin (x) cos^(n−3) (x) +((n−1)/n)∙((n−3)/(n−2))∙(1/(n−4))sin (x) cos^(n−5) (x) +...... +((n−1)/n)∙((n−3)/(n−2))∙((n−5)/(n−4))∙∙∙(5/6)∙(1/4)sin (x) cos^3 (x) +((n−1)/n)∙((n−3)/(n−2))∙((n−5)/(n−4))∙∙∙(5/6)∙(3/4)∙(1/2)sin (x) cos (x) +((n−1)/n)∙((n−3)/(n−2))∙((n−5)/(n−4))∙∙∙(5/6)∙(3/4)∙(1/2)x+C =𝚺_(k=1) ^(n/2) (((n−1)(n−3)∙∙∙(n−2k+3)^(=1 if k=1) )/(n(n−2)∙∙∙(n−2k+2)))∙ sin (x) cos^(n−2k+1) (x) +(((n−1)!!)/(n!!))x+C if n is odd we get: I_n =∫cos^n (x) dx =(1/n) sin (x) cos^(n−1) (x) +((n−1)/n)∙(1/(n−2)) sin (x) cos^(n−3) (x) +((n−1)/n)∙((n−3)/(n−2))∙(1/(n−4)) sin (x) cos^(n−5) (x) +...... +((n−1)/n)∙((n−3)/(n−2))∙((n−5)/(n−4))∙∙∙(4/5)∙(1/3) sin (x) cos^2 (x) +((n−1)/n)∙((n−3)/(n−2))∙((n−5)/(n−4))∙∙∙(4/5)∙(2/3)∙(1/1) sin (x) cos^0 (x)+C =𝚺_(k=1) ^((n+1)/2) (((n−1)(n−3)∙∙∙(n−2k+1)^(=1 if k=1) )/(n(n−2)∙∙∙(n−2k+2)))∙ sin (x) cos^(n−2k+1) (x)+C
$${If}\:{n}\:{is}\:{even}\:{we}\:{get}: \\ $$$${I}_{{n}} =\int\mathrm{cos}^{{n}} \:\left({x}\right)\:{dx} \\ $$$$=\frac{\mathrm{1}}{{n}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{\mathrm{1}}{{n}−\mathrm{2}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{3}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{\mathrm{1}}{{n}−\mathrm{4}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{5}} \:\left({x}\right) \\ $$$$+…… \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{{n}−\mathrm{5}}{{n}−\mathrm{4}}\centerdot\centerdot\centerdot\frac{\mathrm{5}}{\mathrm{6}}\centerdot\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{\mathrm{3}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{{n}−\mathrm{5}}{{n}−\mathrm{4}}\centerdot\centerdot\centerdot\frac{\mathrm{5}}{\mathrm{6}}\centerdot\frac{\mathrm{3}}{\mathrm{4}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}\:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{{n}−\mathrm{5}}{{n}−\mathrm{4}}\centerdot\centerdot\centerdot\frac{\mathrm{5}}{\mathrm{6}}\centerdot\frac{\mathrm{3}}{\mathrm{4}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}{x}+{C} \\ $$$$=\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\frac{\boldsymbol{{n}}}{\mathrm{2}}} {\boldsymbol{\sum}}}\frac{\overset{=\mathrm{1}\:{if}\:{k}=\mathrm{1}} {\left(\boldsymbol{{n}}−\mathrm{1}\right)\left(\boldsymbol{{n}}−\mathrm{3}\right)\centerdot\centerdot\centerdot\left(\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{3}\right)}}{\boldsymbol{{n}}\left(\boldsymbol{{n}}−\mathrm{2}\right)\centerdot\centerdot\centerdot\left(\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{2}\right)}\centerdot\:\boldsymbol{\mathrm{sin}}\:\left(\boldsymbol{{x}}\right)\:\boldsymbol{\mathrm{cos}}^{\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{1}} \:\left(\boldsymbol{{x}}\right) \\ $$$$+\frac{\left(\boldsymbol{{n}}−\mathrm{1}\right)!!}{\boldsymbol{{n}}!!}\boldsymbol{{x}}+\boldsymbol{{C}} \\ $$$$ \\ $$$${if}\:{n}\:{is}\:{odd}\:{we}\:{get}: \\ $$$${I}_{{n}} =\int\mathrm{cos}^{{n}} \:\left({x}\right)\:{dx} \\ $$$$=\frac{\mathrm{1}}{{n}}\:\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{\mathrm{1}}{{n}−\mathrm{2}}\:\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{3}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{\mathrm{1}}{{n}−\mathrm{4}}\:\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{5}} \:\left({x}\right) \\ $$$$+…… \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{{n}−\mathrm{5}}{{n}−\mathrm{4}}\centerdot\centerdot\centerdot\frac{\mathrm{4}}{\mathrm{5}}\centerdot\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{\mathrm{2}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{{n}−\mathrm{5}}{{n}−\mathrm{4}}\centerdot\centerdot\centerdot\frac{\mathrm{4}}{\mathrm{5}}\centerdot\frac{\mathrm{2}}{\mathrm{3}}\centerdot\frac{\mathrm{1}}{\mathrm{1}}\:\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{\mathrm{0}} \:\left({x}\right)+{C} \\ $$$$=\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\frac{\boldsymbol{{n}}+\mathrm{1}}{\mathrm{2}}} {\boldsymbol{\sum}}}\frac{\overset{=\mathrm{1}\:{if}\:{k}=\mathrm{1}} {\left(\boldsymbol{{n}}−\mathrm{1}\right)\left(\boldsymbol{{n}}−\mathrm{3}\right)\centerdot\centerdot\centerdot\left(\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{1}\right)}}{\boldsymbol{{n}}\left(\boldsymbol{{n}}−\mathrm{2}\right)\centerdot\centerdot\centerdot\left(\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{2}\right)}\centerdot\:\boldsymbol{\mathrm{sin}}\:\left(\boldsymbol{{x}}\right)\:\boldsymbol{\mathrm{cos}}^{\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{1}} \:\left(\boldsymbol{{x}}\right)+\boldsymbol{{C}} \\ $$
Commented by tawa tawa last updated on 27/May/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 27/May/17
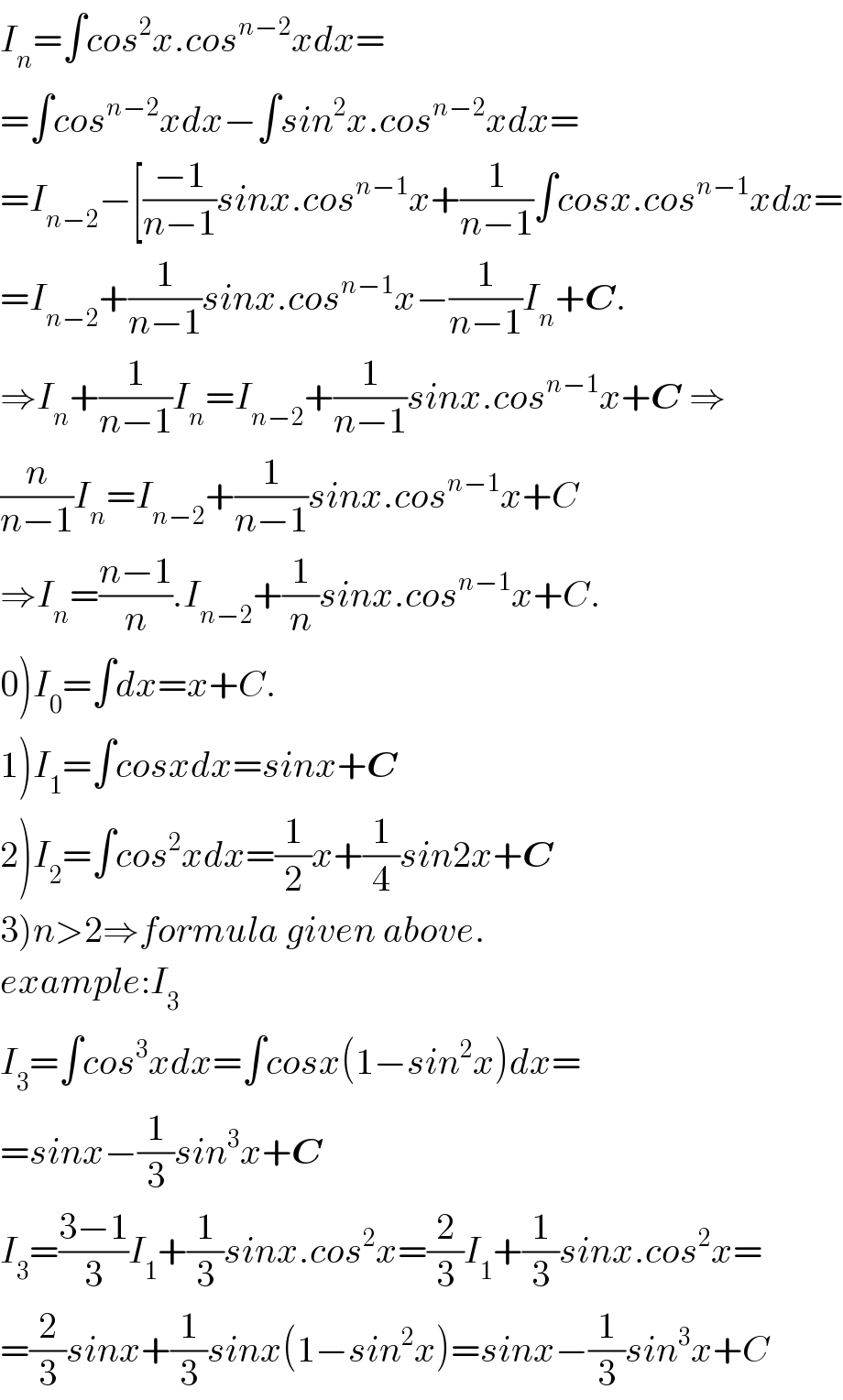
I_n =∫cos^2 x.cos^(n−2) xdx= =∫cos^(n−2) xdx−∫sin^2 x.cos^(n−2) xdx= =I_(n−2) −[((−1)/(n−1))sinx.cos^(n−1) x+(1/(n−1))∫cosx.cos^(n−1) xdx= =I_(n−2) +(1/(n−1))sinx.cos^(n−1) x−(1/(n−1))I_n +C. ⇒I_n +(1/(n−1))I_n =I_(n−2) +(1/(n−1))sinx.cos^(n−1) x+C ⇒ (n/(n−1))I_n =I_(n−2) +(1/(n−1))sinx.cos^(n−1) x+C ⇒I_n =((n−1)/n).I_(n−2) +(1/n)sinx.cos^(n−1) x+C. 0)I_0 =∫dx=x+C. 1)I_1 =∫cosxdx=sinx+C 2)I_2 =∫cos^2 xdx=(1/2)x+(1/4)sin2x+C 3)n>2⇒formula given above. example:I_3 I_3 =∫cos^3 xdx=∫cosx(1−sin^2 x)dx= =sinx−(1/3)sin^3 x+C I_3 =((3−1)/3)I_1 +(1/3)sinx.cos^2 x=(2/3)I_1 +(1/3)sinx.cos^2 x= =(2/3)sinx+(1/3)sinx(1−sin^2 x)=sinx−(1/3)sin^3 x+C
$${I}_{{n}} =\int{cos}^{\mathrm{2}} {x}.{cos}^{{n}−\mathrm{2}} {xdx}= \\ $$$$=\int{cos}^{{n}−\mathrm{2}} {xdx}−\int{sin}^{\mathrm{2}} {x}.{cos}^{{n}−\mathrm{2}} {xdx}= \\ $$$$={I}_{{n}−\mathrm{2}} −\left[\frac{−\mathrm{1}}{{n}−\mathrm{1}}{sinx}.{cos}^{{n}−\mathrm{1}} {x}+\frac{\mathrm{1}}{{n}−\mathrm{1}}\int{cosx}.{cos}^{{n}−\mathrm{1}} {xdx}=\right. \\ $$$$={I}_{{n}−\mathrm{2}} +\frac{\mathrm{1}}{{n}−\mathrm{1}}{sinx}.{cos}^{{n}−\mathrm{1}} {x}−\frac{\mathrm{1}}{{n}−\mathrm{1}}{I}_{{n}} +\boldsymbol{{C}}. \\ $$$$\Rightarrow{I}_{{n}} +\frac{\mathrm{1}}{{n}−\mathrm{1}}{I}_{{n}} ={I}_{{n}−\mathrm{2}} +\frac{\mathrm{1}}{{n}−\mathrm{1}}{sinx}.{cos}^{{n}−\mathrm{1}} {x}+\boldsymbol{{C}}\:\Rightarrow \\ $$$$\frac{{n}}{{n}−\mathrm{1}}{I}_{{n}} ={I}_{{n}−\mathrm{2}} +\frac{\mathrm{1}}{{n}−\mathrm{1}}{sinx}.{cos}^{{n}−\mathrm{1}} {x}+{C} \\ $$$$\Rightarrow{I}_{{n}} =\frac{{n}−\mathrm{1}}{{n}}.{I}_{{n}−\mathrm{2}} +\frac{\mathrm{1}}{{n}}{sinx}.{cos}^{{n}−\mathrm{1}} {x}+{C}. \\ $$$$\left.\mathrm{0}\right){I}_{\mathrm{0}} =\int{dx}={x}+{C}. \\ $$$$\left.\mathrm{1}\right){I}_{\mathrm{1}} =\int{cosxdx}={sinx}+\boldsymbol{{C}} \\ $$$$\left.\mathrm{2}\right){I}_{\mathrm{2}} =\int{cos}^{\mathrm{2}} {xdx}=\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{2}{x}+\boldsymbol{{C}} \\ $$$$\left.\mathrm{3}\right){n}>\mathrm{2}\Rightarrow{formula}\:{given}\:{above}. \\ $$$${example}:{I}_{\mathrm{3}} \\ $$$${I}_{\mathrm{3}} =\int{cos}^{\mathrm{3}} {xdx}=\int{cosx}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right){dx}= \\ $$$$={sinx}−\frac{\mathrm{1}}{\mathrm{3}}{sin}^{\mathrm{3}} {x}+\boldsymbol{{C}} \\ $$$${I}_{\mathrm{3}} =\frac{\mathrm{3}−\mathrm{1}}{\mathrm{3}}{I}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{3}}{sinx}.{cos}^{\mathrm{2}} {x}=\frac{\mathrm{2}}{\mathrm{3}}{I}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{3}}{sinx}.{cos}^{\mathrm{2}} {x}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{sinx}+\frac{\mathrm{1}}{\mathrm{3}}{sinx}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)={sinx}−\frac{\mathrm{1}}{\mathrm{3}}{sin}^{\mathrm{3}} {x}+{C} \\ $$
Commented by tawa tawa last updated on 27/May/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *