Menu Close

cos-sin-cos-d-

Tinku Tara 0 Comments
Pin




Question Number 102183 by bemath last updated on 07/Jul/20
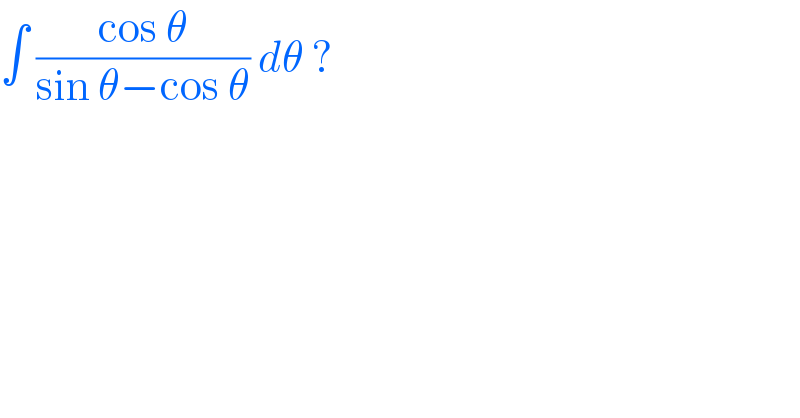
∫ ((cos θ)/(sin θ−cos θ)) dθ ?
$$\int\:\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta−\mathrm{cos}\:\theta}\:{d}\theta\:? \\ $$
Answered by Dwaipayan Shikari last updated on 07/Jul/20
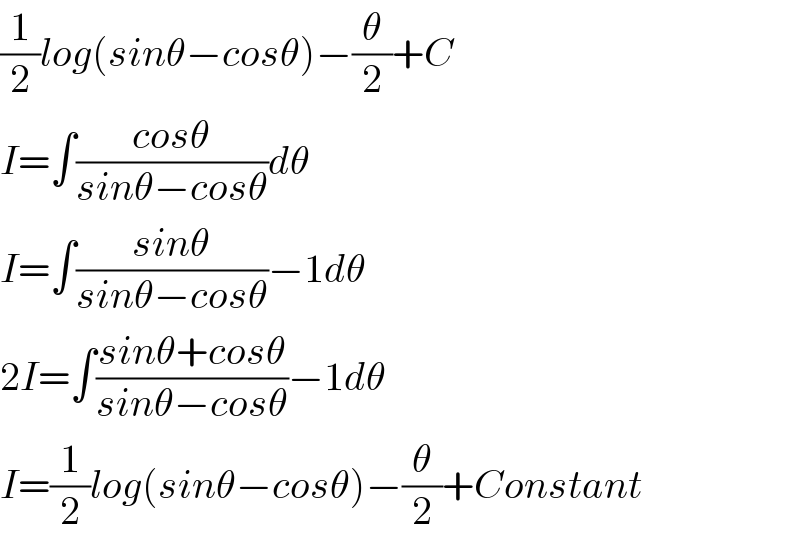
(1/2)log(sinθ−cosθ)−(θ/2)+C I=∫((cosθ)/(sinθ−cosθ))dθ I=∫((sinθ)/(sinθ−cosθ))−1dθ 2I=∫((sinθ+cosθ)/(sinθ−cosθ))−1dθ I=(1/2)log(sinθ−cosθ)−(θ/2)+Constant
$$\frac{\mathrm{1}}{\mathrm{2}}{log}\left({sin}\theta−{cos}\theta\right)−\frac{\theta}{\mathrm{2}}+{C} \\ $$$${I}=\int\frac{{cos}\theta}{{sin}\theta−{cos}\theta}{d}\theta \\ $$$${I}=\int\frac{{sin}\theta}{{sin}\theta−{cos}\theta}−\mathrm{1}{d}\theta \\ $$$$\mathrm{2}{I}=\int\frac{{sin}\theta+{cos}\theta}{{sin}\theta−{cos}\theta}−\mathrm{1}{d}\theta \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{log}\left({sin}\theta−{cos}\theta\right)−\frac{\theta}{\mathrm{2}}+{Constant} \\ $$
Answered by bobhans last updated on 07/Jul/20
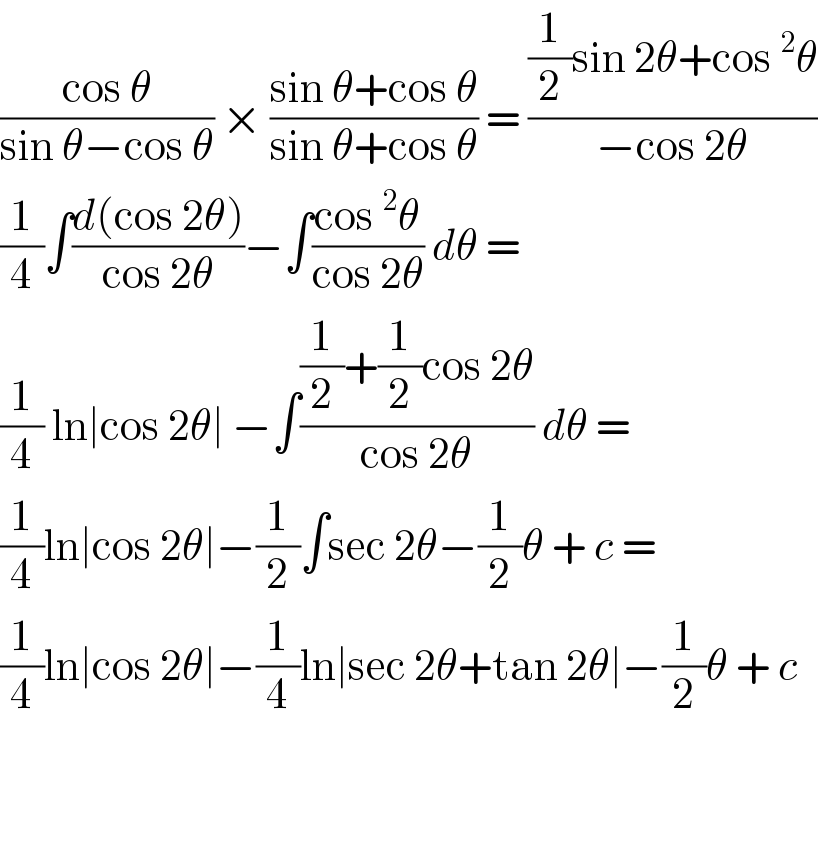
((cos θ)/(sin θ−cos θ)) × ((sin θ+cos θ)/(sin θ+cos θ)) = (((1/2)sin 2θ+cos^2 θ)/(−cos 2θ)) (1/4)∫((d(cos 2θ))/(cos 2θ))−∫((cos^2 θ)/(cos 2θ)) dθ = (1/4) ln∣cos 2θ∣ −∫(((1/2)+(1/2)cos 2θ)/(cos 2θ)) dθ = (1/4)ln∣cos 2θ∣−(1/2)∫sec 2θ−(1/2)θ + c = (1/4)ln∣cos 2θ∣−(1/4)ln∣sec 2θ+tan 2θ∣−(1/2)θ + c
$$\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta−\mathrm{cos}\:\theta}\:×\:\frac{\mathrm{sin}\:\theta+\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta+\mathrm{cos}\:\theta}\:=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta+\mathrm{cos}\:^{\mathrm{2}} \theta}{−\mathrm{cos}\:\mathrm{2}\theta} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{d}\left(\mathrm{cos}\:\mathrm{2}\theta\right)}{\mathrm{cos}\:\mathrm{2}\theta}−\int\frac{\mathrm{cos}\:^{\mathrm{2}} \theta}{\mathrm{cos}\:\mathrm{2}\theta}\:{d}\theta\:=\: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{ln}\mid\mathrm{cos}\:\mathrm{2}\theta\mid\:−\int\frac{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{cos}\:\mathrm{2}\theta}\:{d}\theta\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{cos}\:\mathrm{2}\theta\mid−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{sec}\:\mathrm{2}\theta−\frac{\mathrm{1}}{\mathrm{2}}\theta\:+\:{c}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{cos}\:\mathrm{2}\theta\mid−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\mid\mathrm{sec}\:\mathrm{2}\theta+\mathrm{tan}\:\mathrm{2}\theta\mid−\frac{\mathrm{1}}{\mathrm{2}}\theta\:+\:{c} \\ $$$$ \\ $$$$ \\ $$
Answered by 1549442205 last updated on 07/Jul/20
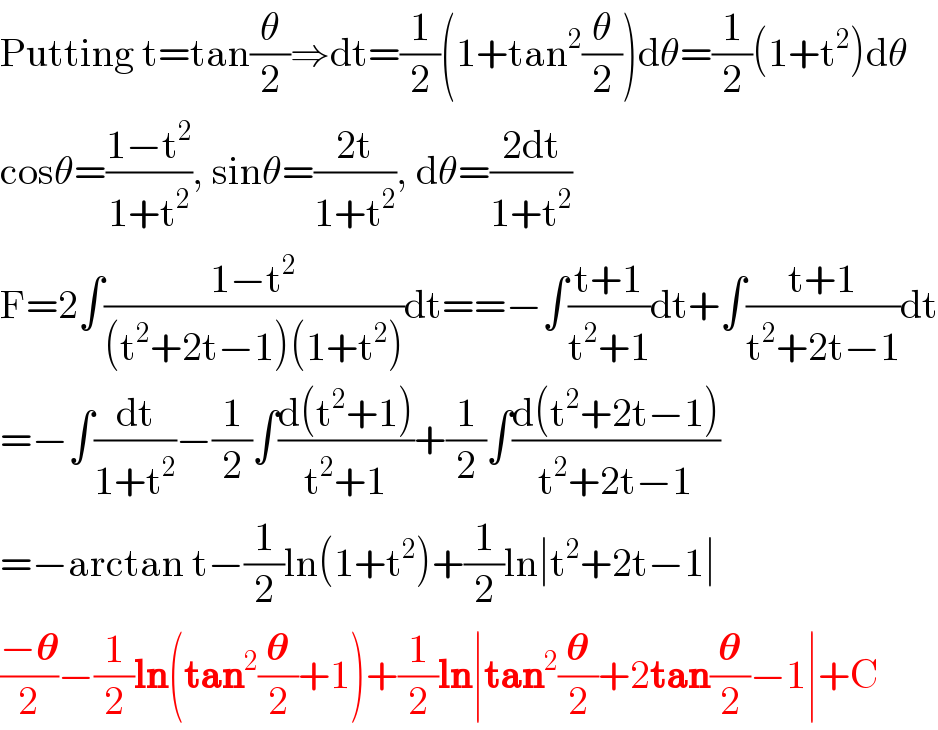
Putting t=tan(θ/2)⇒dt=(1/2)(1+tan^2 (θ/2))dθ=(1/2)(1+t^2 )dθ cosθ=((1−t^2 )/(1+t^2 )), sinθ=((2t)/(1+t^2 )), dθ=((2dt)/(1+t^2 )) F=2∫((1−t^2 )/((t^2 +2t−1)(1+t^2 )))dt==−∫((t+1)/(t^2 +1))dt+∫((t+1)/(t^2 +2t−1))dt =−∫(dt/(1+t^2 ))−(1/2)∫((d(t^2 +1))/(t^2 +1))+(1/2)∫((d(t^2 +2t−1))/(t^2 +2t−1)) =−arctan t−(1/2)ln(1+t^2 )+(1/2)ln∣t^2 +2t−1∣ ((−𝛉)/2)−(1/2)ln(tan^2 (𝛉/2)+1)+(1/2)ln∣tan^2 (𝛉/2)+2tan(𝛉/2)−1∣+C
$$\mathrm{Putting}\:\mathrm{t}=\mathrm{tan}\frac{\theta}{\mathrm{2}}\Rightarrow\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}\right)\mathrm{d}\theta=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\mathrm{d}\theta \\ $$$$\mathrm{cos}\theta=\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} },\:\mathrm{sin}\theta=\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} },\:\mathrm{d}\theta=\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\mathrm{F}=\mathrm{2}\int\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{2t}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{dt}==−\int\frac{\mathrm{t}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\mathrm{dt}+\int\frac{\mathrm{t}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{2t}−\mathrm{1}}\mathrm{dt} \\ $$$$=−\int\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{d}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{d}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{2t}−\mathrm{1}\right)}{\mathrm{t}^{\mathrm{2}} +\mathrm{2t}−\mathrm{1}} \\ $$$$=−\mathrm{arctan}\:\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{t}^{\mathrm{2}} +\mathrm{2t}−\mathrm{1}\mid \\ $$$$\frac{−\boldsymbol{\theta}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \frac{\boldsymbol{\theta}}{\mathrm{2}}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{ln}}\mid\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \frac{\boldsymbol{\theta}}{\mathrm{2}}+\mathrm{2}\boldsymbol{\mathrm{tan}}\frac{\boldsymbol{\theta}}{\mathrm{2}}−\mathrm{1}\mid+\mathrm{C} \\ $$
Answered by mathmax by abdo last updated on 08/Jul/20
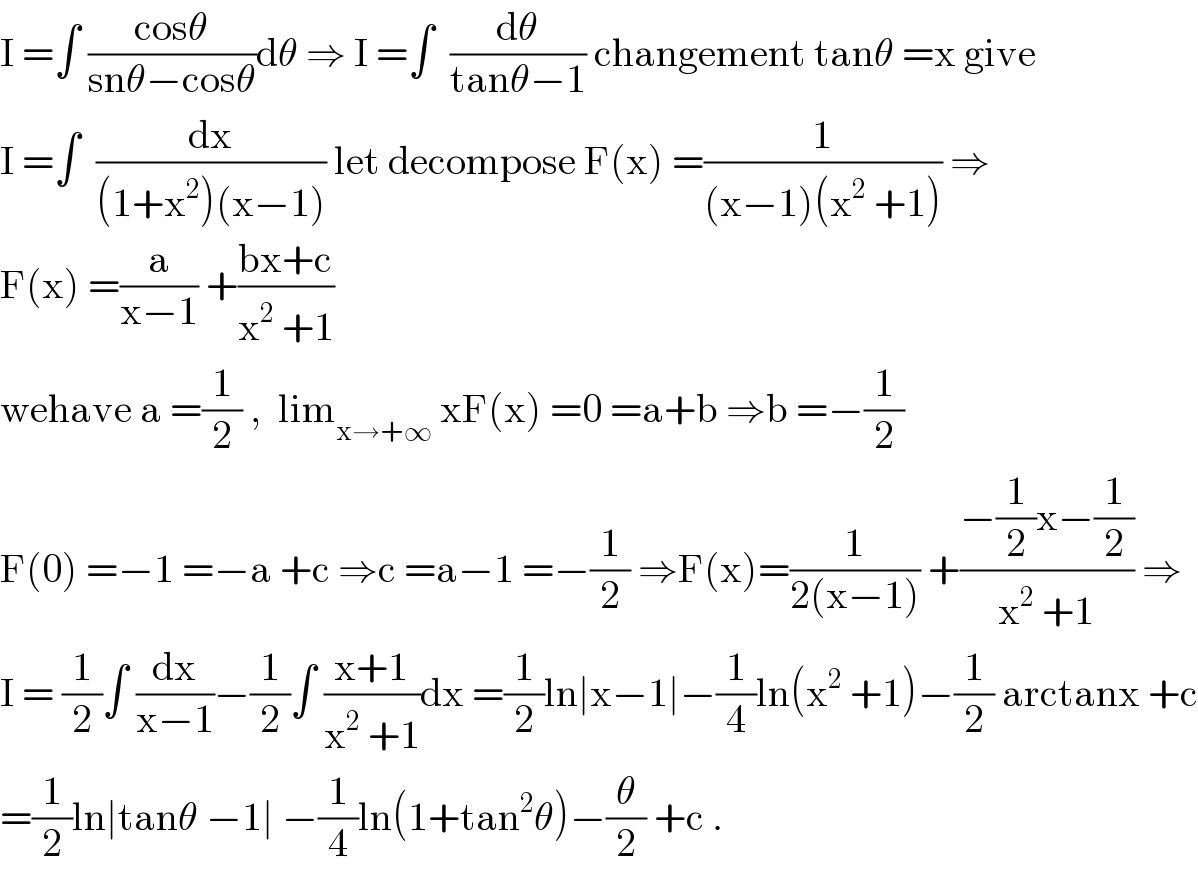
I =∫ ((cosθ)/(snθ−cosθ))dθ ⇒ I =∫ (dθ/(tanθ−1)) changement tanθ =x give I =∫ (dx/((1+x^2 )(x−1))) let decompose F(x) =(1/((x−1)(x^2 +1))) ⇒ F(x) =(a/(x−1)) +((bx+c)/(x^2 +1)) wehave a =(1/2) , lim_(x→+∞) xF(x) =0 =a+b ⇒b =−(1/2) F(0) =−1 =−a +c ⇒c =a−1 =−(1/2) ⇒F(x)=(1/(2(x−1))) +((−(1/2)x−(1/2))/(x^2 +1)) ⇒ I = (1/2)∫ (dx/(x−1))−(1/2)∫ ((x+1)/(x^2 +1))dx =(1/2)ln∣x−1∣−(1/4)ln(x^2 +1)−(1/2) arctanx +c =(1/2)ln∣tanθ −1∣ −(1/4)ln(1+tan^2 θ)−(θ/2) +c .
$$\mathrm{I}\:=\int\:\frac{\mathrm{cos}\theta}{\mathrm{sn}\theta−\mathrm{cos}\theta}\mathrm{d}\theta\:\Rightarrow\:\mathrm{I}\:=\int\:\:\frac{\mathrm{d}\theta}{\mathrm{tan}\theta−\mathrm{1}}\:\mathrm{changement}\:\mathrm{tan}\theta\:=\mathrm{x}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{x}−\mathrm{1}\right)}\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{a}}{\mathrm{x}−\mathrm{1}}\:+\frac{\mathrm{bx}+\mathrm{c}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{wehave}\:\mathrm{a}\:=\frac{\mathrm{1}}{\mathrm{2}}\:,\:\:\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\mathrm{xF}\left(\mathrm{x}\right)\:=\mathrm{0}\:=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{F}\left(\mathrm{0}\right)\:=−\mathrm{1}\:=−\mathrm{a}\:+\mathrm{c}\:\Rightarrow\mathrm{c}\:=\mathrm{a}−\mathrm{1}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)}\:+\frac{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{dx}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{arctanx}\:+\mathrm{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{tan}\theta\:−\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)−\frac{\theta}{\mathrm{2}}\:+\mathrm{c}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *