Question Number 162112 by amin96 last updated on 26/Dec/21
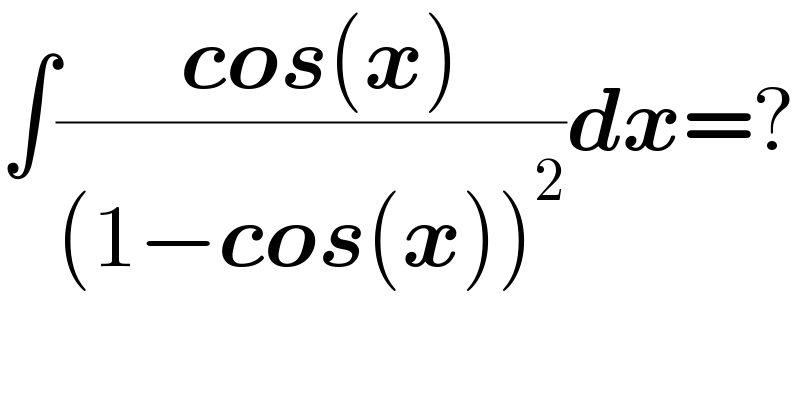
$$\int\frac{\:\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)}{\left(\mathrm{1}−\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)\right)^{\mathrm{2}} }\boldsymbol{{dx}}=? \\ $$
Answered by Ar Brandon last updated on 26/Dec/21
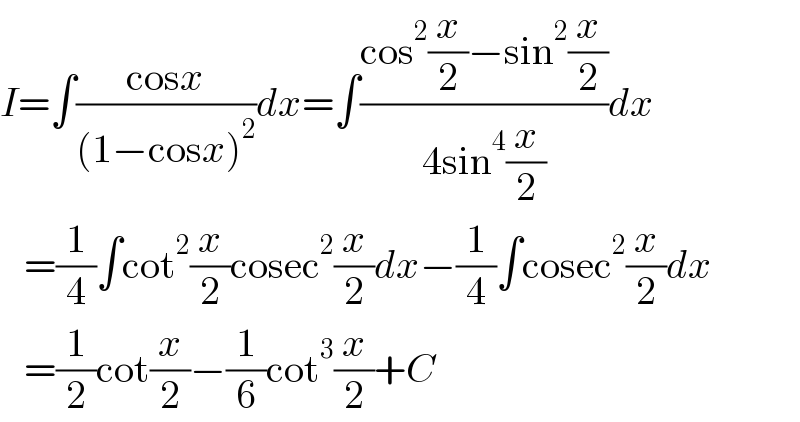
$${I}=\int\frac{\mathrm{cos}{x}}{\left(\mathrm{1}−\mathrm{cos}{x}\right)^{\mathrm{2}} }{dx}=\int\frac{\mathrm{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{4sin}^{\mathrm{4}} \frac{{x}}{\mathrm{2}}}{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int\mathrm{cot}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\mathrm{cosec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}−\frac{\mathrm{1}}{\mathrm{4}}\int\mathrm{cosec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cot}\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{cot}^{\mathrm{3}} \frac{{x}}{\mathrm{2}}+{C} \\ $$
