Question Number 17377 by tawa tawa last updated on 04/Jul/17
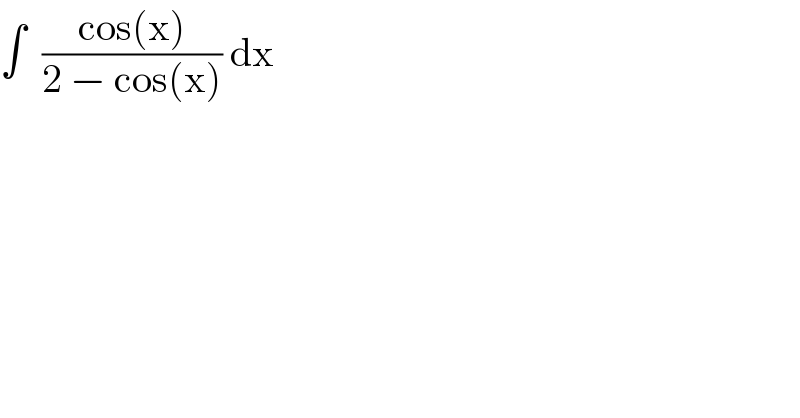
$$\int\:\:\frac{\mathrm{cos}\left(\mathrm{x}\right)}{\mathrm{2}\:−\:\mathrm{cos}\left(\mathrm{x}\right)}\:\mathrm{dx} \\ $$
Answered by ajfour last updated on 05/Jul/17
![cos x=((1−tan^2 (x/2))/(1+tan^2 (x/2))) =((2(1−t^2 ))/(1+t^2 )) if we let tan (x/2)=t dt=(1/2)sec^2 (x/2)dx=((1+tan^2 (x/2))/2)dx dt =((1+t^2 )/2)dx ⇒ dx=((2dt)/(1+t^2 )) I=∫((cos x)/(2−cos x)) dx =∫(((((1−t^2 )/(1+t^2 ))))/(2−(((1−t^2 )/(1+t^2 )))))(((2dt)/(1+t^2 ))) =∫((2(1−t^2 ))/((1+t^2 )(2+2t^2 −1+t^2 )))dt =∫((2(1−t^2 )dt)/((1+t^2 )(3t^2 +1))) I=∫(A/(1+t^2 ))dt+∫(B/(3t^2 +1))dt A=((2(1−t^2 ))/(3t^2 +1))∣_(t^2 =−1) = 1 B=((2(1−t^2 ))/(1+t^2 ))∣_(t^2 =−1/3) =((2(4/3))/(10/3))=(4/5) I=∫(dt/(1+t^2 ))+(4/(15))∫(dt/(t^2 +(1/(√)3)^2 )) =tan^(−1) t+(4/(15))×(√3) tan^(−1) (t(√3))+C I=(x/2)+(4/(5(√3)))tan^(−1) [(√3)tan (x/2)]+C.](https://www.tinkutara.com/question/Q17378.png)
$$\mathrm{cos}\:\mathrm{x}=\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\left(\mathrm{x}/\mathrm{2}\right)}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{x}/\mathrm{2}\right)}\:=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{let}\:\mathrm{tan}\:\left(\mathrm{x}/\mathrm{2}\right)=\mathrm{t} \\ $$$$\:\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{x}/\mathrm{2}\right)\mathrm{dx}=\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{x}/\mathrm{2}\right)}{\mathrm{2}}\mathrm{dx} \\ $$$$\mathrm{dt}\:\:=\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\mathrm{dx}\:\:\Rightarrow\:\:\mathrm{dx}=\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$\mathrm{I}=\int\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{2}−\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\:=\int\frac{\left(\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)}{\mathrm{2}−\left(\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)}\left(\frac{\mathrm{2dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right) \\ $$$$=\int\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{2}+\mathrm{2t}^{\mathrm{2}} −\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{dt} \\ $$$$=\int\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{3t}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\mathrm{I}=\int\frac{\mathrm{A}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}+\int\frac{\mathrm{B}}{\mathrm{3t}^{\mathrm{2}} +\mathrm{1}}\mathrm{dt} \\ $$$$\mathrm{A}=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{3t}^{\mathrm{2}} +\mathrm{1}}\mid_{\mathrm{t}^{\mathrm{2}} =−\mathrm{1}} =\:\mathrm{1} \\ $$$$\mathrm{B}=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mid_{\mathrm{t}^{\mathrm{2}} =−\mathrm{1}/\mathrm{3}} \:=\frac{\mathrm{2}\left(\mathrm{4}/\mathrm{3}\right)}{\mathrm{10}/\mathrm{3}}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{I}=\int\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{15}}\int\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\left(\mathrm{1}/\sqrt{}\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\:=\mathrm{tan}^{−\mathrm{1}} \mathrm{t}+\frac{\mathrm{4}}{\mathrm{15}}×\sqrt{\mathrm{3}}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{t}\sqrt{\mathrm{3}}\right)+\mathrm{C} \\ $$$$\mathrm{I}=\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{4}}{\mathrm{5}\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left[\sqrt{\mathrm{3}}\mathrm{tan}\:\left(\mathrm{x}/\mathrm{2}\right)\right]+\mathrm{C}. \\ $$
Commented by tawa tawa last updated on 05/Jul/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
