Question Number 58346 by ANTARES VY last updated on 21/Apr/19
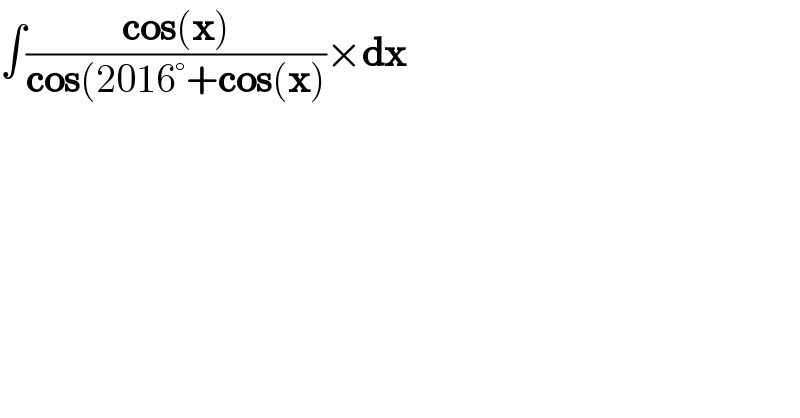
$$\int\frac{\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{cos}}\left(\mathrm{2016}°+\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)\right.}×\boldsymbol{\mathrm{dx}} \\ $$
Answered by ANTARES VY last updated on 21/Apr/19

$$\boldsymbol{\mathrm{F}}\left(\boldsymbol{\mathrm{x}}\right)=? \\ $$
Answered by tanmay last updated on 23/Apr/19
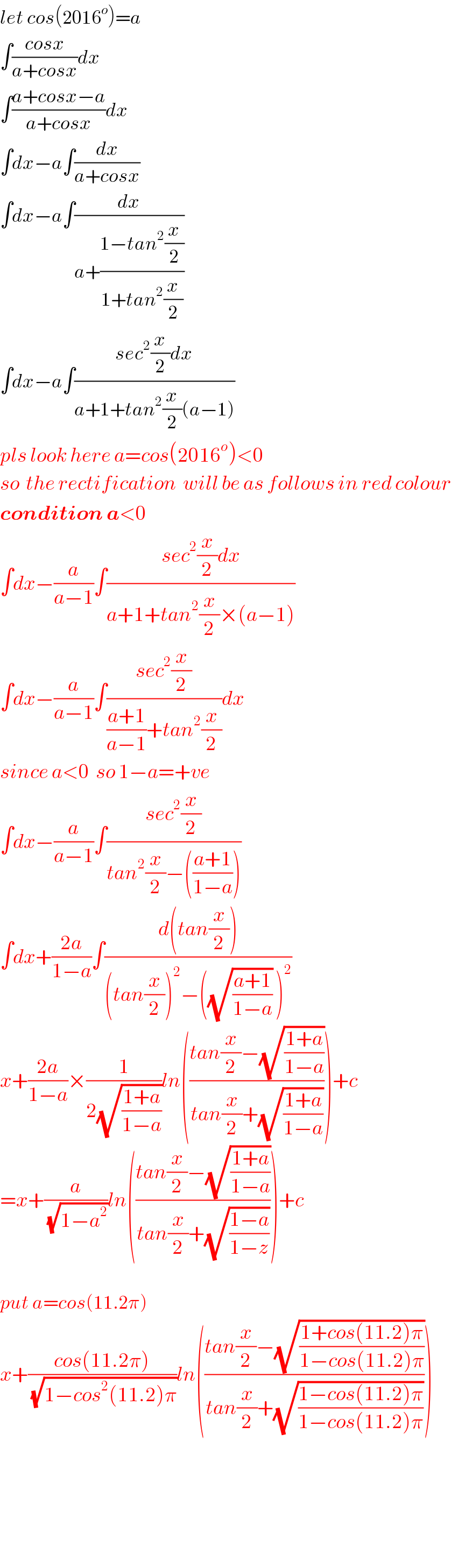
$${let}\:{cos}\left(\mathrm{2016}^{{o}} \right)={a} \\ $$$$\int\frac{{cosx}}{{a}+{cosx}}{dx} \\ $$$$\int\frac{{a}+{cosx}−{a}}{{a}+{cosx}}{dx} \\ $$$$\int{dx}−{a}\int\frac{{dx}}{{a}+{cosx}} \\ $$$$\int{dx}−{a}\int\frac{{dx}}{{a}+\frac{\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}} \\ $$$$\int{dx}−{a}\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}}{{a}+\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\left({a}−\mathrm{1}\right)} \\ $$$${pls}\:{look}\:{here}\:{a}={cos}\left(\mathrm{2016}^{{o}} \right)<\mathrm{0} \\ $$$${so}\:\:{the}\:{rectification}\:\:{will}\:{be}\:{as}\:{follows}\:{in}\:{red}\:{colour} \\ $$$$\boldsymbol{{condition}}\:\boldsymbol{{a}}<\mathrm{0} \\ $$$$\int{dx}−\frac{{a}}{{a}−\mathrm{1}}\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}}{{a}+\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}×\left({a}−\mathrm{1}\right)} \\ $$$$\int{dx}−\frac{{a}}{{a}−\mathrm{1}}\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx} \\ $$$${since}\:{a}<\mathrm{0}\:\:{so}\:\mathrm{1}−{a}=+{ve} \\ $$$$\int{dx}−\frac{{a}}{{a}−\mathrm{1}}\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\left(\frac{{a}+\mathrm{1}}{\mathrm{1}−{a}}\right)} \\ $$$$\int{dx}+\frac{\mathrm{2}{a}}{\mathrm{1}−{a}}\int\frac{{d}\left({tan}\frac{{x}}{\mathrm{2}}\right)}{\left({tan}\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\sqrt{\frac{{a}+\mathrm{1}}{\mathrm{1}−{a}}}\:\right)^{\mathrm{2}} } \\ $$$${x}+\frac{\mathrm{2}{a}}{\mathrm{1}−{a}}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}}{ln}\left(\frac{{tan}\frac{{x}}{\mathrm{2}}−\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}}{{tan}\frac{{x}}{\mathrm{2}}+\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}}\right)+{c} \\ $$$$={x}+\frac{{a}}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}{ln}\left(\frac{{tan}\frac{{x}}{\mathrm{2}}−\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}}{{tan}\frac{{x}}{\mathrm{2}}+\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}−{z}}}}\right)+{c} \\ $$$$ \\ $$$${put}\:{a}={cos}\left(\mathrm{11}.\mathrm{2}\pi\right) \\ $$$${x}+\frac{{cos}\left(\mathrm{11}.\mathrm{2}\pi\right)}{\:\sqrt{\mathrm{1}−{cos}^{\mathrm{2}} \left(\mathrm{11}.\mathrm{2}\right)\pi}}{ln}\left(\frac{{tan}\frac{{x}}{\mathrm{2}}−\sqrt{\frac{\mathrm{1}+{cos}\left(\mathrm{11}.\mathrm{2}\right)\pi}{\mathrm{1}−{cos}\left(\mathrm{11}.\mathrm{2}\right)\pi}}}{{tan}\frac{{x}}{\mathrm{2}}+\sqrt{\frac{\mathrm{1}−{cos}\left(\mathrm{11}.\mathrm{2}\right)\pi}{\mathrm{1}−{cos}\left(\mathrm{11}.\mathrm{2}\right)\pi}}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 23/Apr/19
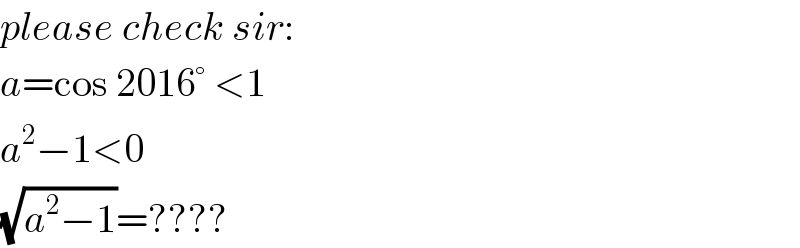
$${please}\:{check}\:{sir}: \\ $$$${a}=\mathrm{cos}\:\mathrm{2016}°\:<\mathrm{1} \\ $$$${a}^{\mathrm{2}} −\mathrm{1}<\mathrm{0} \\ $$$$\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}=???? \\ $$
Commented by tanmay last updated on 23/Apr/19

$${i}\:{have}\:{not}\:{checked}\:{the}\:{value}\:{of}\:{cos}\left(\mathrm{2016}^{{o}} \right) \\ $$$${yes}\:{cos}\left(\mathrm{2016}^{{o}} \right)<\mathrm{0} \\ $$$${so}\:{a}<\mathrm{1}\: \\ $$$${hence}\:{the}\:{rectification}\:{will}\:{be}\:{added}\:{in}\:{red}\:{colour} \\ $$$$ \\ $$
