Question Number 147810 by mathdanisur last updated on 23/Jul/21
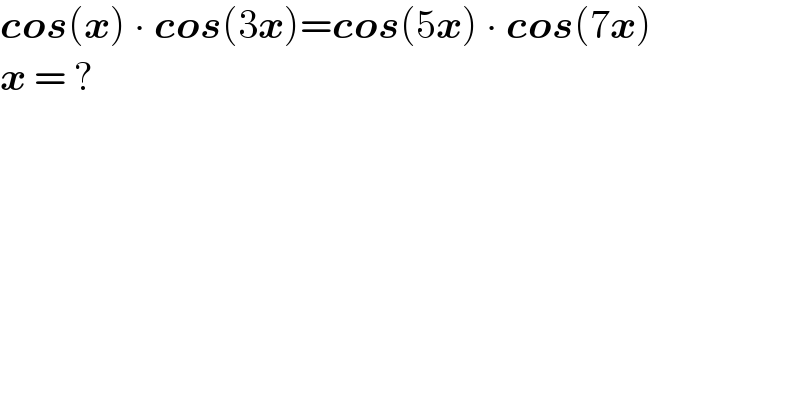
$$\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)\:\centerdot\:\boldsymbol{{cos}}\left(\mathrm{3}\boldsymbol{{x}}\right)=\boldsymbol{{cos}}\left(\mathrm{5}\boldsymbol{{x}}\right)\:\centerdot\:\boldsymbol{{cos}}\left(\mathrm{7}\boldsymbol{{x}}\right) \\ $$$$\boldsymbol{{x}}\:=\:? \\ $$
Answered by gsk2684 last updated on 23/Jul/21
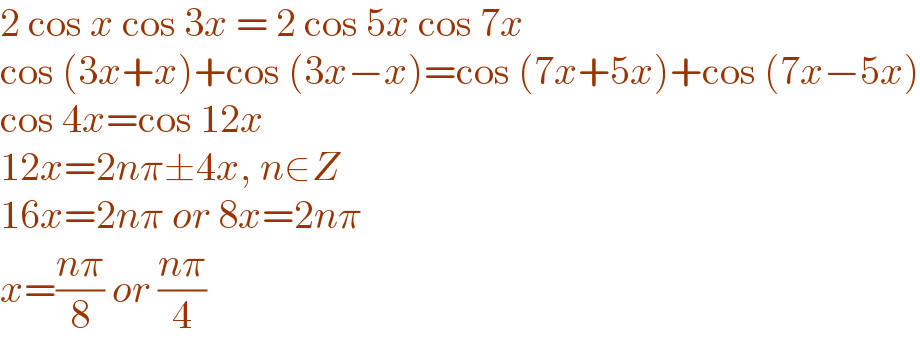
$$\mathrm{2}\:\mathrm{cos}\:{x}\:\mathrm{cos}\:\mathrm{3}{x}\:=\:\mathrm{2}\:\mathrm{cos}\:\mathrm{5}{x}\:\mathrm{cos}\:\mathrm{7}{x} \\ $$$$\mathrm{cos}\:\left(\mathrm{3}{x}+{x}\right)+\mathrm{cos}\:\left(\mathrm{3}{x}−{x}\right)=\mathrm{cos}\:\left(\mathrm{7}{x}+\mathrm{5}{x}\right)+\mathrm{cos}\:\left(\mathrm{7}{x}−\mathrm{5}{x}\right) \\ $$$$\mathrm{cos}\:\mathrm{4}{x}=\mathrm{cos}\:\mathrm{12}{x} \\ $$$$\mathrm{12}{x}=\mathrm{2}{n}\pi\pm\mathrm{4}{x},\:{n}\in{Z} \\ $$$$\mathrm{16}{x}=\mathrm{2}{n}\pi\:{or}\:\mathrm{8}{x}=\mathrm{2}{n}\pi \\ $$$${x}=\frac{{n}\pi}{\mathrm{8}}\:{or}\:\frac{{n}\pi}{\mathrm{4}} \\ $$
Commented by mathdanisur last updated on 23/Jul/21

$${Thank}\:{you}\:{Sir} \\ $$
Commented by peter frank last updated on 24/Jul/21

$${thank}\:{you} \\ $$
