Question Number 129519 by BHOOPENDRA last updated on 16/Jan/21
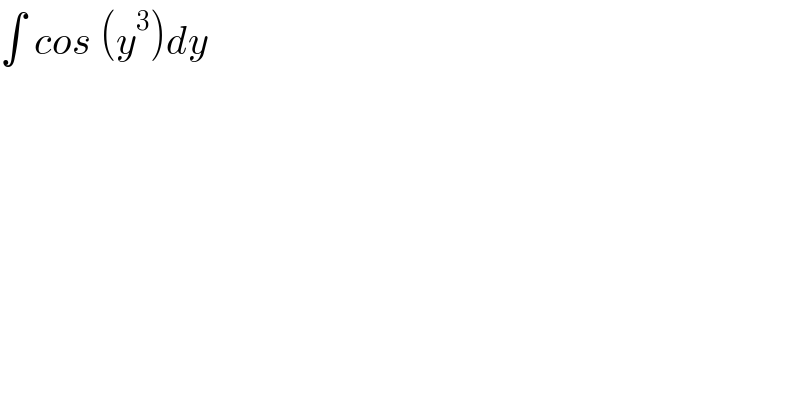
$$\int\:{cos}\:\left({y}^{\mathrm{3}} \right){dy} \\ $$
Answered by Dwaipayan Shikari last updated on 16/Jan/21
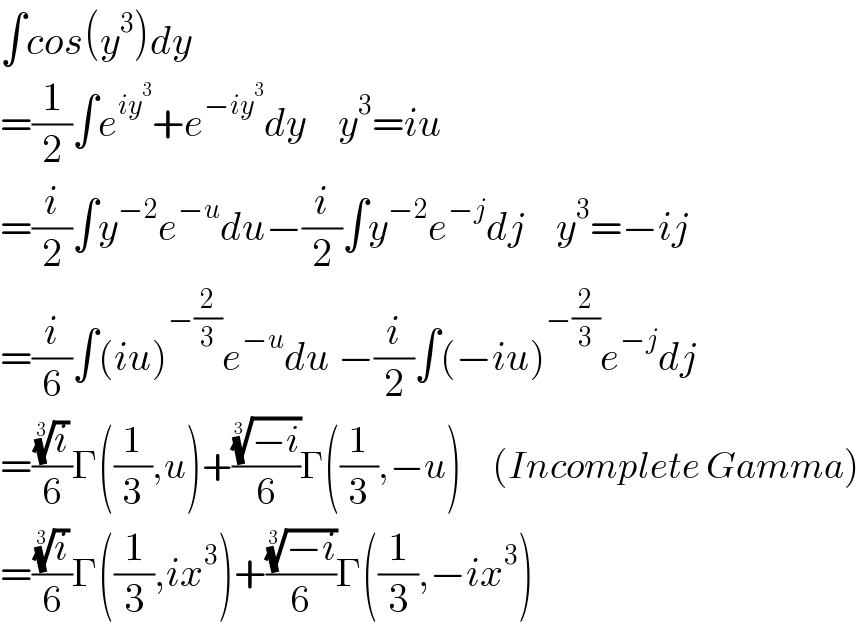
$$\int{cos}\left({y}^{\mathrm{3}} \right){dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{e}^{{iy}^{\mathrm{3}} } +{e}^{−{iy}^{\mathrm{3}} } {dy}\:\:\:\:{y}^{\mathrm{3}} ={iu} \\ $$$$=\frac{{i}}{\mathrm{2}}\int{y}^{−\mathrm{2}} {e}^{−{u}} {du}−\frac{{i}}{\mathrm{2}}\int{y}^{−\mathrm{2}} {e}^{−{j}} {dj}\:\:\:\:{y}^{\mathrm{3}} =−{ij} \\ $$$$=\frac{{i}}{\mathrm{6}}\int\left({iu}\right)^{−\frac{\mathrm{2}}{\mathrm{3}}} {e}^{−{u}} {du}\:−\frac{{i}}{\mathrm{2}}\int\left(−{iu}\right)^{−\frac{\mathrm{2}}{\mathrm{3}}} {e}^{−{j}} {dj} \\ $$$$=\frac{\sqrt[{\mathrm{3}}]{{i}}}{\mathrm{6}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}},{u}\right)+\frac{\sqrt[{\mathrm{3}}]{−{i}}}{\mathrm{6}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}},−{u}\right)\:\:\:\:\:\left({Incomplete}\:{Gamma}\right) \\ $$$$=\frac{\sqrt[{\mathrm{3}}]{{i}}}{\mathrm{6}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}},{ix}^{\mathrm{3}} \right)+\frac{\sqrt[{\mathrm{3}}]{−{i}}}{\mathrm{6}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}},−{ix}^{\mathrm{3}} \right) \\ $$
