Question Number 103299 by B. H 28 last updated on 14/Jul/20
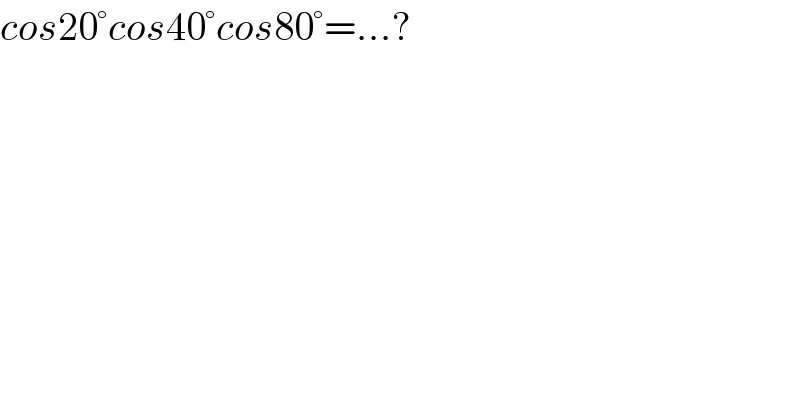
$${cos}\mathrm{20}°{cos}\mathrm{40}°{cos}\mathrm{80}°=…? \\ $$
Answered by bemath last updated on 14/Jul/20
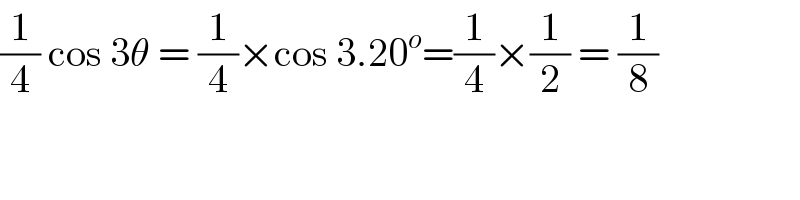
$$\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{cos}\:\mathrm{3}\theta\:=\:\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{cos}\:\mathrm{3}.\mathrm{20}^{{o}} =\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Answered by Dwaipayan Shikari last updated on 14/Jul/20

$$\frac{\mathrm{1}}{\mathrm{2}{sin}\mathrm{20}°}\left({sin}\mathrm{40}°{cos}\mathrm{40}°{cos}\mathrm{80}°\right)=\frac{\mathrm{1}}{\mathrm{4}{sin}\mathrm{20}°}\left({sin}\mathrm{80}°{cos}\mathrm{80}°\right)=\frac{{sin}\mathrm{160}°}{\mathrm{8}{sin}\mathrm{20}°}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
