Menu Close

cos3x-1-x-2-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 100746 by Rohit@Thakur last updated on 28/Jun/20
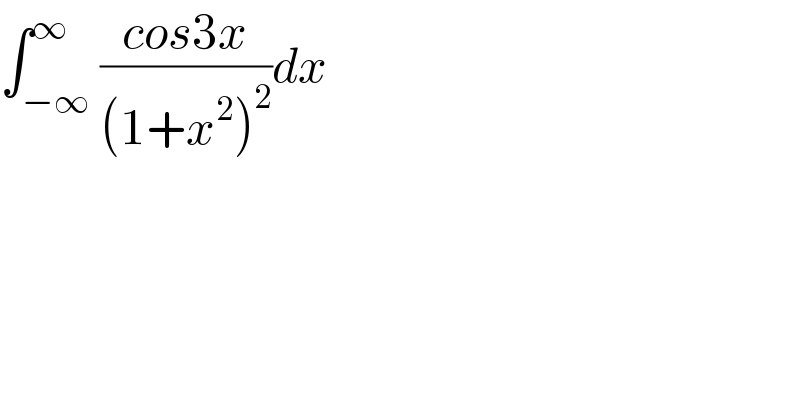
∫_(−∞) ^∞ ((cos3x)/((1+x^2 )^2 ))dx
$$\int_{−\infty} ^{\infty} \frac{{cos}\mathrm{3}{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$
Answered by mathmax by abdo last updated on 28/Jun/20
A =∫_(−∞) ^(+∞) ((cos(3x))/((x^2 +1)^2 ))dx ⇒ A =Re(∫_(−∞) ^(+∞) (e^(3ix) /((x^2 +1)^2 ))dx) let ϕ(z)=(e^(3iz) /((z^2 +1)^2 )) we have ∣ϕ(z)z∣ →0 (z→∞) and ϕ(z) =(e^(3iz) /((z−i)^2 (z+i)^2 )) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,i) Res(ϕ,i) =lim_(z→i) (1/((2−1)!)){(z−i)^2 ϕ(z)}^((1)) =lim_(z→i) {(e^(i3z) /((z+i)^2 ))}^((1)) =lim_(z→i) ((3ie^(i3z) (z+i)^2 −2(z+i)e^(i3z) )/((z+i)^4 )) =lim_(z→i) ((3ie^(i3z) (z+i)−2 e^(i3z) )/((z+i)^3 )) =lim_(z→i) (((3i(z+i)−2)e^(i3z) )/((z+i)^3 )) =(((3i(2i)−2)e^(i(3i)) )/((2i)^3 )) =(((−6−2)e^(−3) )/(−8i)) =(e^(−3) /i) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ×(e^(−3) /i) =2π e^(−3) ⇒ A =((2π)/e^3 )
$$\mathrm{A}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cos}\left(\mathrm{3x}\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\:\mathrm{A}\:=\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{3ix}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\right)\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{3iz}} }{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\mid\varphi\left(\mathrm{z}\right)\mathrm{z}\mid\:\rightarrow\mathrm{0}\:\left(\mathrm{z}\rightarrow\infty\right)\:\mathrm{and}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{e}^{\mathrm{3iz}} }{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give}\:\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{i}\right) \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\:\left\{\frac{\mathrm{e}^{\mathrm{i3z}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\mathrm{3ie}^{\mathrm{i3z}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)\mathrm{e}^{\mathrm{i3z}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} } \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\:\:\frac{\mathrm{3ie}^{\mathrm{i3z}} \left(\mathrm{z}+\mathrm{i}\right)−\mathrm{2}\:\mathrm{e}^{\mathrm{i3z}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} }\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\frac{\left(\mathrm{3i}\left(\mathrm{z}+\mathrm{i}\right)−\mathrm{2}\right)\mathrm{e}^{\mathrm{i3z}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left(\mathrm{3i}\left(\mathrm{2i}\right)−\mathrm{2}\right)\mathrm{e}^{\mathrm{i}\left(\mathrm{3i}\right)} }{\left(\mathrm{2i}\right)^{\mathrm{3}} }\:=\frac{\left(−\mathrm{6}−\mathrm{2}\right)\mathrm{e}^{−\mathrm{3}} }{−\mathrm{8i}}\:=\frac{\mathrm{e}^{−\mathrm{3}} }{\mathrm{i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi×\frac{\mathrm{e}^{−\mathrm{3}} }{\mathrm{i}}\:=\mathrm{2}\pi\:\mathrm{e}^{−\mathrm{3}} \:\Rightarrow\:\mathrm{A}\:=\frac{\mathrm{2}\pi}{\mathrm{e}^{\mathrm{3}} } \\ $$
Commented by Rohit@Thakur last updated on 28/Jun/20
thanks sir
$${thanks}\:{sir} \\ $$
Commented by Rohit@Thakur last updated on 28/Jun/20
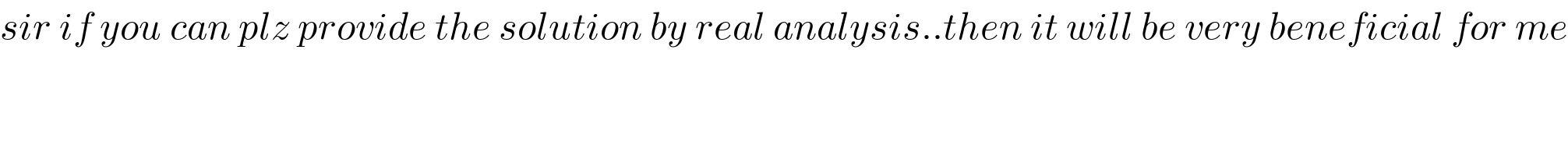
sir if you can plz provide the solution by real analysis..then it will be very beneficial for me
$${sir}\:{if}\:{you}\:{can}\:{plz}\:{provide}\:{the}\:{solution}\:{by}\:{real}\:{analysis}..{then}\:{it}\:{will}\:{be}\:{very}\:{beneficial}\:{for}\:{me} \\ $$
Commented by abdomathmax last updated on 28/Jun/20
impossible to solve this kind of integral with elementary functions...
$$\mathrm{impossible}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{integral}\:\mathrm{with} \\ $$$$\mathrm{elementary}\:\mathrm{functions}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *