Question Number 94574 by student work last updated on 19/May/20
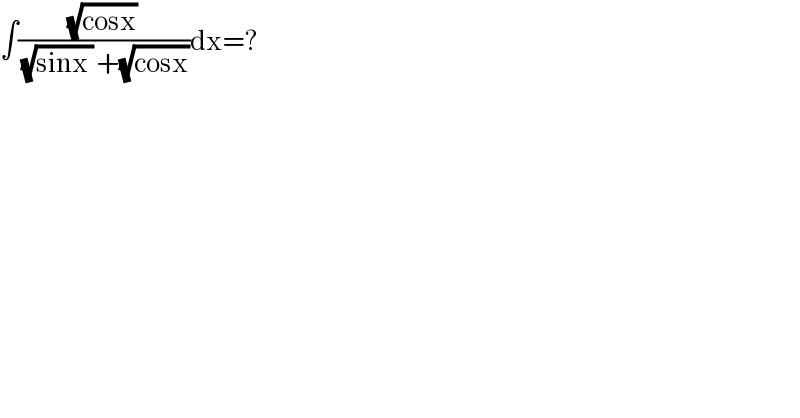
$$\int\frac{\sqrt{\mathrm{cosx}}}{\:\sqrt{\mathrm{sinx}\:}\:+\sqrt{\mathrm{cosx}}}\mathrm{dx}=? \\ $$
Commented by student work last updated on 19/May/20

$$\mathrm{please}\:\mathrm{solve}\:\mathrm{who}\:\mathrm{can}? \\ $$
Answered by MJS last updated on 19/May/20
![∫((√(cos x))/( (√(sin x))+(√(cos x))))dx= [t=(√(tan x)) → dx=2cos^2 x (√(tan x)) dt] =2∫(t/((t^4 +1)(t+1)))dt= =∫((t^3 −t^2 +t+1)/(t^4 +1))dt+∫(dt/(t+1))= =((1−(√2))/2)∫((t−1−(√2))/(t^2 −(√2)t+1))dt+((1+(√2))/2)∫((t−1+(√2))/(t^2 +(√2)t+1))dt−∫(dt/(t+1)) now it should be easy](https://www.tinkutara.com/question/Q94593.png)
$$\int\frac{\sqrt{\mathrm{cos}\:{x}}}{\:\sqrt{\mathrm{sin}\:{x}}+\sqrt{\mathrm{cos}\:{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{tan}\:{x}}\:\rightarrow\:{dx}=\mathrm{2cos}^{\mathrm{2}} \:{x}\:\sqrt{\mathrm{tan}\:{x}}\:{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}}{\left({t}^{\mathrm{4}} +\mathrm{1}\right)\left({t}+\mathrm{1}\right)}{dt}= \\ $$$$=\int\frac{{t}^{\mathrm{3}} −{t}^{\mathrm{2}} +{t}+\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{1}}{dt}+\int\frac{{dt}}{{t}+\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}−\mathrm{1}−\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt}+\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}−\mathrm{1}+\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt}−\int\frac{{dt}}{{t}+\mathrm{1}} \\ $$$$\mathrm{now}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{easy} \\ $$
Commented by student work last updated on 20/May/20
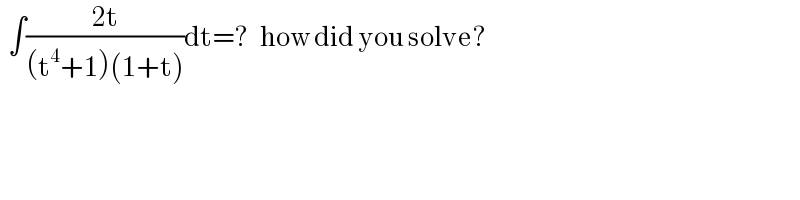
$$\:\:\int\frac{\mathrm{2t}}{\left(\mathrm{t}^{\mathrm{4}} +\mathrm{1}\right)\left(\mathrm{1}+\mathrm{t}\right)}\mathrm{dt}=?\:\:\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{solve}? \\ $$
Commented by MJS last updated on 20/May/20

$$\mathrm{just}\:\mathrm{decompose} \\ $$
