Question Number 94119 by i jagooll last updated on 17/May/20
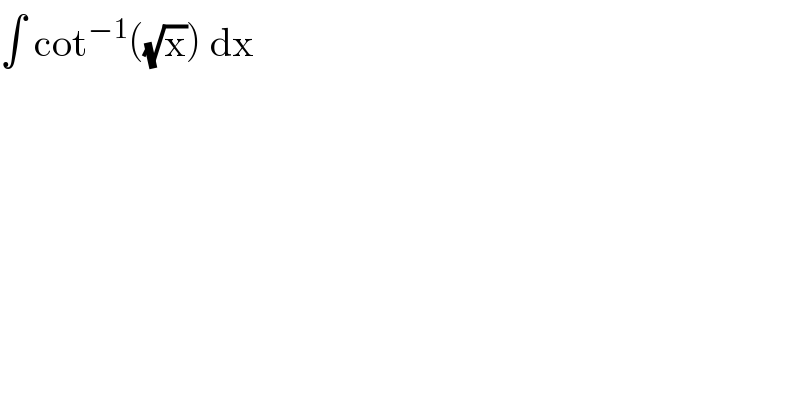
$$\int\:\mathrm{cot}^{−\mathrm{1}} \left(\sqrt{\mathrm{x}}\right)\:\mathrm{dx}\: \\ $$
Commented by i jagooll last updated on 17/May/20
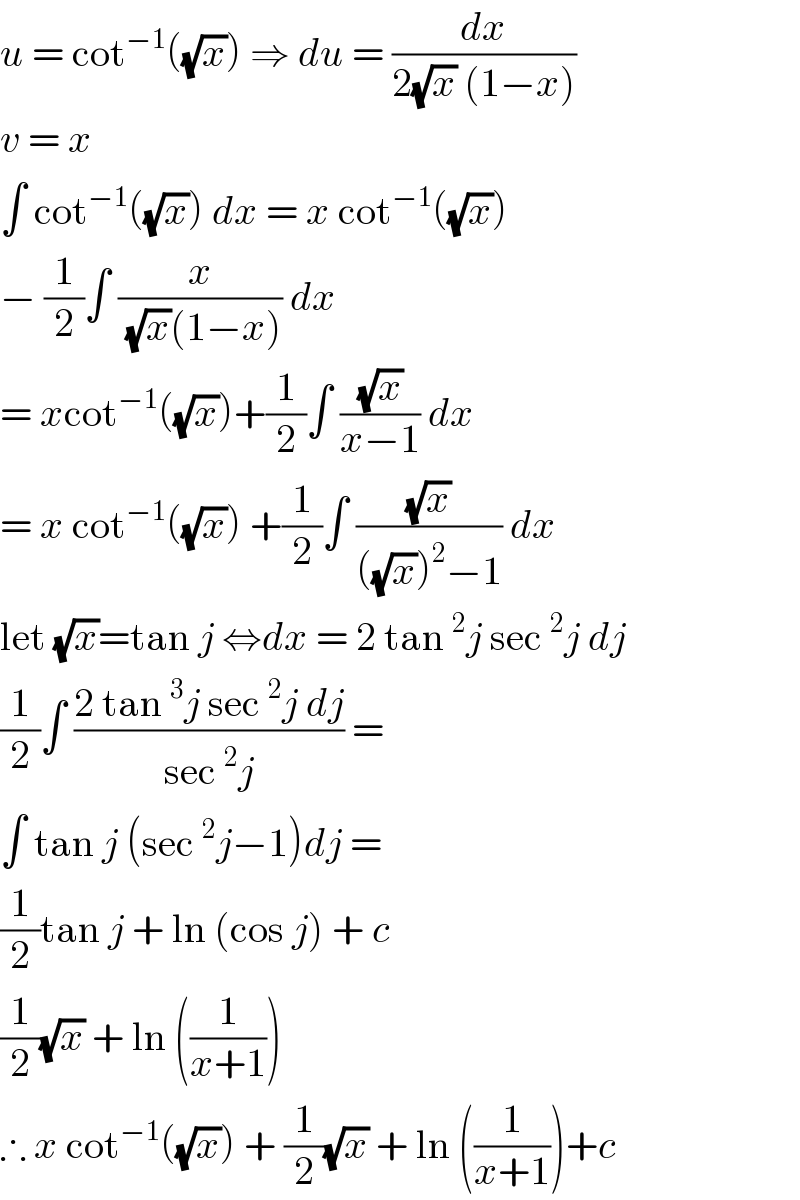
$${u}\:=\:\mathrm{cot}^{−\mathrm{1}} \left(\sqrt{{x}}\right)\:\Rightarrow\:{du}\:=\:\frac{{dx}}{\mathrm{2}\sqrt{{x}}\:\left(\mathrm{1}−{x}\right)} \\ $$$${v}\:=\:{x}\: \\ $$$$\int\:\mathrm{cot}^{−\mathrm{1}} \left(\sqrt{{x}}\right)\:{dx}\:=\:{x}\:\mathrm{cot}^{−\mathrm{1}} \left(\sqrt{{x}}\right)\: \\ $$$$−\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{x}}{\:\sqrt{{x}}\left(\mathrm{1}−{x}\right)}\:{dx}\: \\ $$$$=\:{x}\mathrm{cot}^{−\mathrm{1}} \left(\sqrt{{x}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\sqrt{{x}}}{{x}−\mathrm{1}}\:{dx}\: \\ $$$$=\:{x}\:\mathrm{cot}^{−\mathrm{1}} \left(\sqrt{{x}}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\sqrt{{x}}}{\left(\sqrt{{x}}\right)^{\mathrm{2}} −\mathrm{1}}\:{dx} \\ $$$$\mathrm{let}\:\sqrt{{x}}=\mathrm{tan}\:{j}\:\Leftrightarrow{dx}\:=\:\mathrm{2}\:\mathrm{tan}\:^{\mathrm{2}} {j}\:\mathrm{sec}\:^{\mathrm{2}} {j}\:{dj} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2}\:\mathrm{tan}\:^{\mathrm{3}} {j}\:\mathrm{sec}\:^{\mathrm{2}} {j}\:{dj}}{\mathrm{sec}\:^{\mathrm{2}} {j}}\:=\: \\ $$$$\int\:\mathrm{tan}\:{j}\:\left(\mathrm{sec}\:^{\mathrm{2}} {j}−\mathrm{1}\right){dj}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:{j}\:+\:\mathrm{ln}\:\left(\mathrm{cos}\:{j}\right)\:+\:{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}}\:+\:\mathrm{ln}\:\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)\: \\ $$$$\therefore\:{x}\:\mathrm{cot}^{−\mathrm{1}} \left(\sqrt{{x}}\right)\:+\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{x}}\:+\:\mathrm{ln}\:\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)+{c} \\ $$
