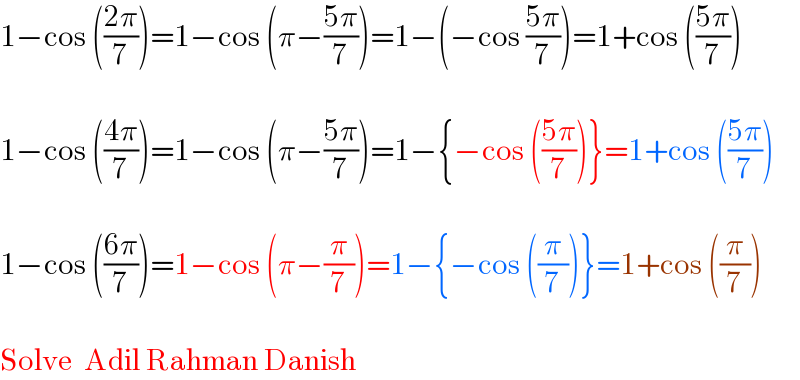Question Number 128582 by john_santu last updated on 08/Jan/21
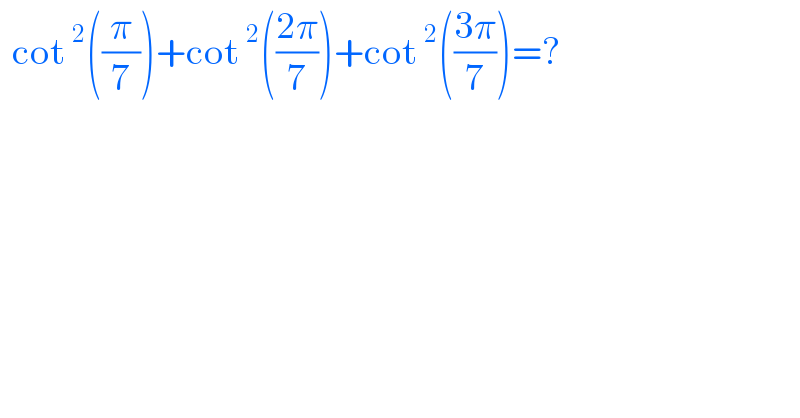
Answered by liberty last updated on 08/Jan/21
![T = cot^2 ((π/7))+cot^2 (((2π)/7))+cot^2 (((3π)/7)) T=csc^2 ((π/7))+csc^2 (((2π)/7))+csc^2 (((3π)/7))−3 T= (1/(sin^2 ((π/7))))+(1/(sin^2 (((2π)/7))))+(1/(sin^2 (((3π)/7))))−3 T = (2/(1−cos (((2π)/7))))+(2/(1−cos (((4π)/7))))+(2/(1−cos (((6π)/7))))−3 T= (2/(1+cos ((π/7))))+(2/(1+cos (((3π)/7))))+(2/(1+cos (((5π)/7))))−3 T= ((2 [ (1+cos (π/7))(1+cos ((3π)/7))+(1+cos (π/7))(1+cos ((5π)/7))+(1+cos ((3π)/7))(1+cos ((5π)/7)) ])/((1+cos (π/7))(1+cos ((3π)/7))(1+cos ((5π)/7))))−3 T= ((2[1+cos (π/7)+cos ((3π)/7)+cos (π/7).cos ((3π)/7)+1+cos (π/7)+cos ((5π)/7)+cos (π/7).cos ((5π)/7)+1+cos ((3π)/7)+cos ((5π)/7)+cos ((3π)/7).cos ((5π)/7) ])/((1+cos ((5π)/7))(1+cos (π/7)+cos ((3π)/7)+cos (π/7).cos ((3π)/7))))−3 T = 8−3 = 5](https://www.tinkutara.com/question/Q128584.png)
Commented by Study last updated on 10/Jan/21
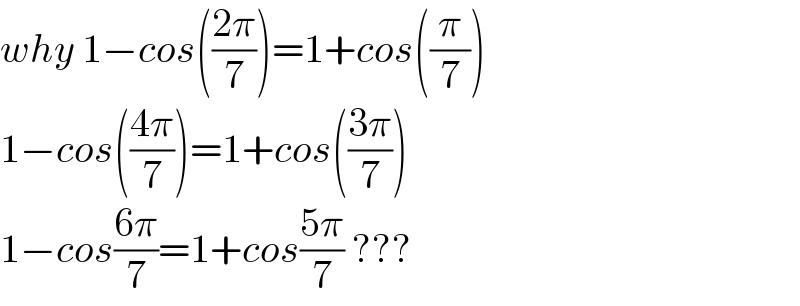
Commented by liberty last updated on 13/Jan/21
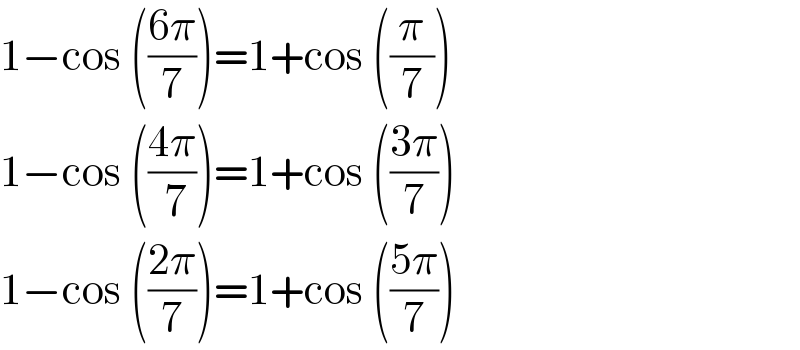
Commented by Adel last updated on 14/Jan/21

Commented by Adel last updated on 14/Jan/21