Question Number 85480 by M±th+et£s last updated on 22/Mar/20

$$\int\frac{{csc}\left({x}\right)}{{cos}\left({x}\right)+{cos}^{\mathrm{3}} \left({x}\right)+…+{cos}^{\mathrm{2}{n}+\mathrm{1}} \left({x}\right)}{dx} \\ $$$$\forall{x}\in{n} \\ $$
Answered by mind is power last updated on 22/Mar/20
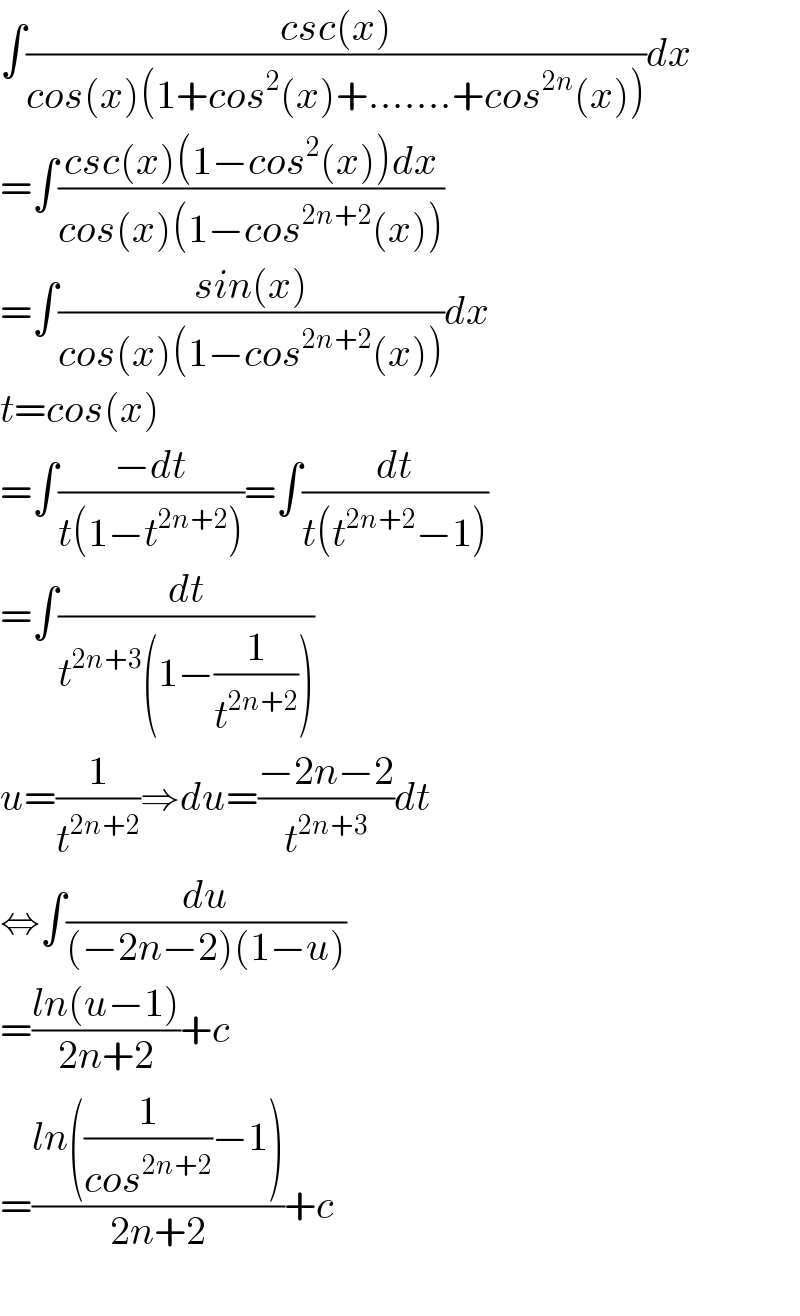
$$\int\frac{{csc}\left({x}\right)}{{cos}\left({x}\right)\left(\mathrm{1}+{cos}^{\mathrm{2}} \left({x}\right)+…….+{cos}^{\mathrm{2}{n}} \left({x}\right)\right)}{dx} \\ $$$$=\int\frac{{csc}\left({x}\right)\left(\mathrm{1}−{cos}^{\mathrm{2}} \left({x}\right)\right){dx}}{{cos}\left({x}\right)\left(\mathrm{1}−{cos}^{\mathrm{2}{n}+\mathrm{2}} \left({x}\right)\right)} \\ $$$$=\int\frac{{sin}\left({x}\right)}{{cos}\left({x}\right)\left(\mathrm{1}−{cos}^{\mathrm{2}{n}+\mathrm{2}} \left({x}\right)\right)}{dx} \\ $$$${t}={cos}\left({x}\right) \\ $$$$=\int\frac{−{dt}}{{t}\left(\mathrm{1}−{t}^{\mathrm{2}{n}+\mathrm{2}} \right)}=\int\frac{{dt}}{{t}\left({t}^{\mathrm{2}{n}+\mathrm{2}} −\mathrm{1}\right)} \\ $$$$=\int\frac{{dt}}{{t}^{\mathrm{2}{n}+\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}{n}+\mathrm{2}} }\right)} \\ $$$${u}=\frac{\mathrm{1}}{{t}^{\mathrm{2}{n}+\mathrm{2}} }\Rightarrow{du}=\frac{−\mathrm{2}{n}−\mathrm{2}}{{t}^{\mathrm{2}{n}+\mathrm{3}} }{dt} \\ $$$$\Leftrightarrow\int\frac{{du}}{\left(−\mathrm{2}{n}−\mathrm{2}\right)\left(\mathrm{1}−{u}\right)} \\ $$$$=\frac{{ln}\left({u}−\mathrm{1}\right)}{\mathrm{2}{n}+\mathrm{2}}+{c} \\ $$$$=\frac{{ln}\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}{n}+\mathrm{2}} }−\mathrm{1}\right)}{\mathrm{2}{n}+\mathrm{2}}+{c} \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 22/Mar/20

$${great}\:{sir}\:{thank}\:{you}\:{so}\:{much} \\ $$
Commented by mind is power last updated on 22/Mar/20

$${withe}\:{pleasur} \\ $$
