Menu Close

cscx-cos-2x-2cos-2-x-dx-pleas-sir-help-me-

Tinku Tara 0 Comments
Pin




Question Number 92421 by mhmd last updated on 06/May/20
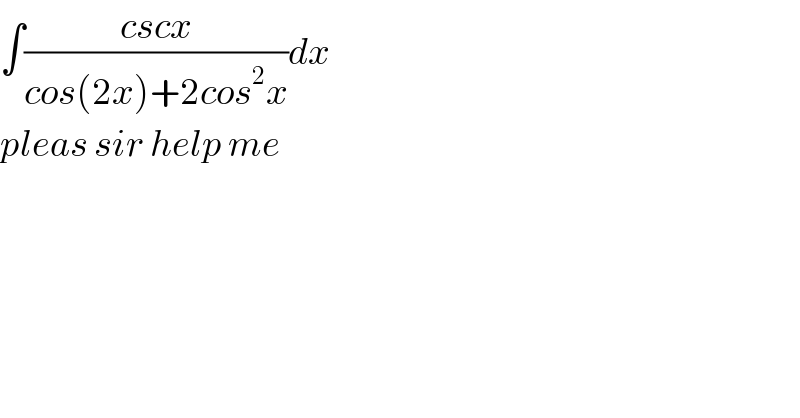
∫((cscx)/(cos(2x)+2cos^2 x))dx pleas sir help me
$$\int\frac{{cscx}}{{cos}\left(\mathrm{2}{x}\right)+\mathrm{2}{cos}^{\mathrm{2}} {x}}{dx} \\ $$$${pleas}\:{sir}\:{help}\:{me} \\ $$
Answered by niroj last updated on 07/May/20
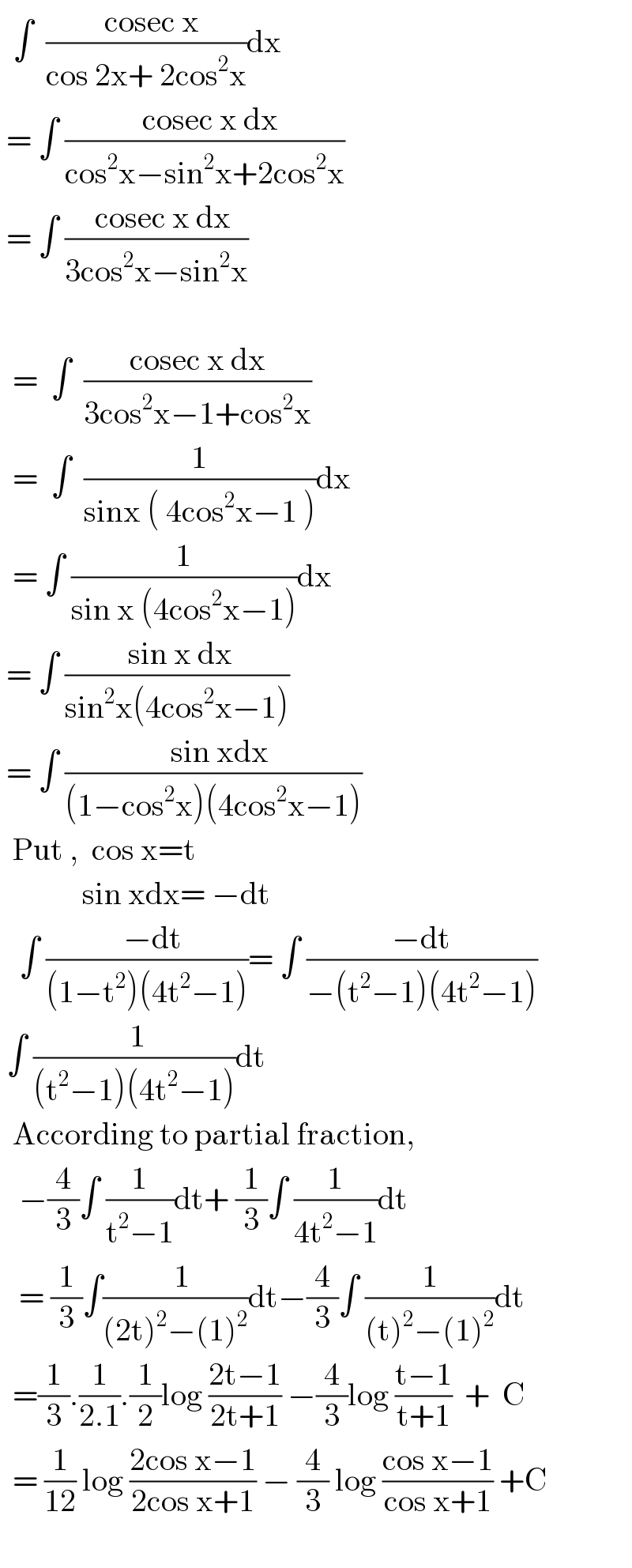
∫ (( cosec x)/(cos 2x+ 2cos^2 x))dx = ∫ (( cosec x dx)/(cos^2 x−sin^2 x+2cos^2 x)) = ∫ (( cosec x dx)/(3cos^2 x−sin^2 x)) = ∫ ((cosec x dx)/(3cos^2 x−1+cos^2 x)) = ∫ (1/(sinx ( 4cos^2 x−1 )))dx = ∫ (1/(sin x (4cos^2 x−1)))dx = ∫ (( sin x dx)/(sin^2 x(4cos^2 x−1))) = ∫ (( sin xdx)/((1−cos^2 x)(4cos^2 x−1))) Put , cos x=t sin xdx= −dt ∫ (( −dt)/((1−t^2 )(4t^2 −1)))= ∫ ((−dt)/(−(t^2 −1)(4t^2 −1))) ∫ (( 1)/((t^2 −1)(4t^2 −1)))dt According to partial fraction, −(4/3)∫ (1/(t^2 −1))dt+ (1/3)∫ (1/(4t^2 −1))dt = (1/3)∫(( 1)/((2t)^2 −(1)^2 ))dt−(4/3)∫ (1/((t)^2 −(1)^2 ))dt =(1/3).(1/(2.1)).(1/2)log ((2t−1)/(2t+1)) −(4/3)log ((t−1)/(t+1)) + C = (1/(12)) log ((2cos x−1)/(2cos x+1)) − (4/3) log ((cos x−1)/(cos x+1)) +C
$$\:\:\int\:\:\frac{\:\:\mathrm{cosec}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{2x}+\:\mathrm{2cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\: \\ $$$$\:=\:\int\:\frac{\:\:\mathrm{cosec}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{2cos}^{\mathrm{2}} \mathrm{x}} \\ $$$$\:=\:\int\:\frac{\:\:\mathrm{cosec}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{3cos}^{\mathrm{2}} \mathrm{x}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}} \\ $$$$\:\:\:\: \\ $$$$\:\:=\:\:\int\:\:\frac{\mathrm{cosec}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{3cos}^{\mathrm{2}} \mathrm{x}−\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}} \\ $$$$\:\:=\:\:\int\:\:\frac{\mathrm{1}}{\mathrm{sinx}\:\left(\:\mathrm{4cos}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\:\right)}\mathrm{dx} \\ $$$$\:\:=\:\int\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{x}\:\left(\mathrm{4cos}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)}\mathrm{dx} \\ $$$$\:=\:\int\:\frac{\:\mathrm{sin}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}\left(\mathrm{4cos}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)} \\ $$$$\:=\:\int\:\frac{\:\:\mathrm{sin}\:\mathrm{xdx}}{\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{4cos}^{\mathrm{2}} \mathrm{x}−\mathrm{1}\right)} \\ $$$$\:\:\mathrm{Put}\:,\:\:\mathrm{cos}\:\mathrm{x}=\mathrm{t} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\:\mathrm{xdx}=\:−\mathrm{dt} \\ $$$$\:\:\:\int\:\frac{\:\:−\mathrm{dt}}{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{4t}^{\mathrm{2}} −\mathrm{1}\right)}=\:\int\:\frac{−\mathrm{dt}}{−\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{4t}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$\:\int\:\frac{\:\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{4t}^{\mathrm{2}} −\mathrm{1}\right)}\mathrm{dt} \\ $$$$\:\:\mathrm{According}\:\mathrm{to}\:\mathrm{partial}\:\mathrm{fraction}, \\ $$$$\:\:\:−\frac{\mathrm{4}}{\mathrm{3}}\int\:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}+\:\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\mathrm{1}}{\mathrm{4t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt} \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\:\:\mathrm{1}}{\left(\mathrm{2t}\right)^{\mathrm{2}} −\left(\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}−\frac{\mathrm{4}}{\mathrm{3}}\int\:\frac{\mathrm{1}}{\left(\mathrm{t}\right)^{\mathrm{2}} −\left(\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{2}.\mathrm{1}}.\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\:\frac{\mathrm{2t}−\mathrm{1}}{\mathrm{2t}+\mathrm{1}}\:−\frac{\mathrm{4}}{\mathrm{3}}\mathrm{log}\:\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}+\mathrm{1}}\:\:+\:\:\mathrm{C} \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{12}}\:\mathrm{log}\:\frac{\mathrm{2cos}\:\mathrm{x}−\mathrm{1}}{\mathrm{2cos}\:\mathrm{x}+\mathrm{1}}\:−\:\frac{\mathrm{4}}{\mathrm{3}}\:\mathrm{log}\:\frac{\mathrm{cos}\:\mathrm{x}−\mathrm{1}}{\mathrm{cos}\:\mathrm{x}+\mathrm{1}}\:+\mathrm{C} \\ $$$$\:\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *