Question Number 185837 by test1234 last updated on 28/Jan/23
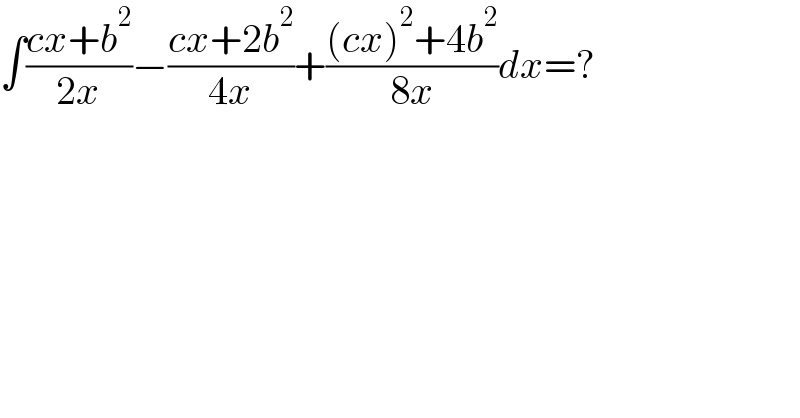
$$\int\frac{{cx}+{b}^{\mathrm{2}} }{\mathrm{2}{x}}−\frac{{cx}+\mathrm{2}{b}^{\mathrm{2}} }{\mathrm{4}{x}}+\frac{\left({cx}\right)^{\mathrm{2}} +\mathrm{4}{b}^{\mathrm{2}} }{\mathrm{8}{x}}{dx}=? \\ $$
Commented by MJS_new last updated on 28/Jan/23
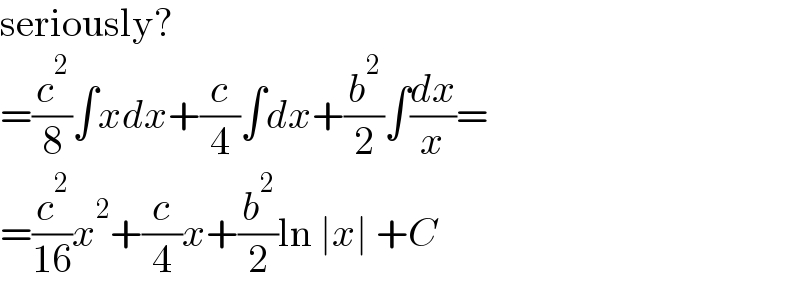
$$\mathrm{seriously}? \\ $$$$=\frac{{c}^{\mathrm{2}} }{\mathrm{8}}\int{xdx}+\frac{{c}}{\mathrm{4}}\int{dx}+\frac{{b}^{\mathrm{2}} }{\mathrm{2}}\int\frac{{dx}}{{x}}= \\ $$$$=\frac{{c}^{\mathrm{2}} }{\mathrm{16}}{x}^{\mathrm{2}} +\frac{{c}}{\mathrm{4}}{x}+\frac{{b}^{\mathrm{2}} }{\mathrm{2}}\mathrm{ln}\:\mid{x}\mid\:+{C} \\ $$
