Menu Close

D-1-2-y-1-y-x-x-pi-

Tinku Tara 0 Comments
Pin




Question Number 104608 by ~blr237~ last updated on 22/Jul/20
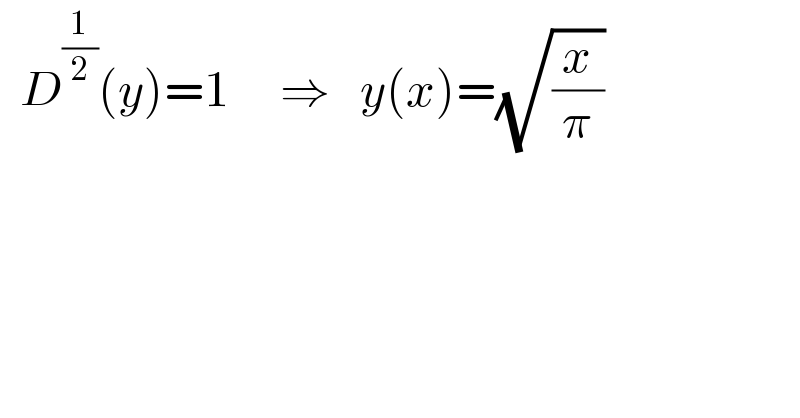
D^(1/2) (y)=1 ⇒ y(x)=(√(x/π))
$$\:\:{D}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({y}\right)=\mathrm{1}\:\:\:\:\:\Rightarrow\:\:\:{y}\left({x}\right)=\sqrt{\frac{{x}}{\pi}} \\ $$
Answered by OlafThorendsen last updated on 22/Jul/20
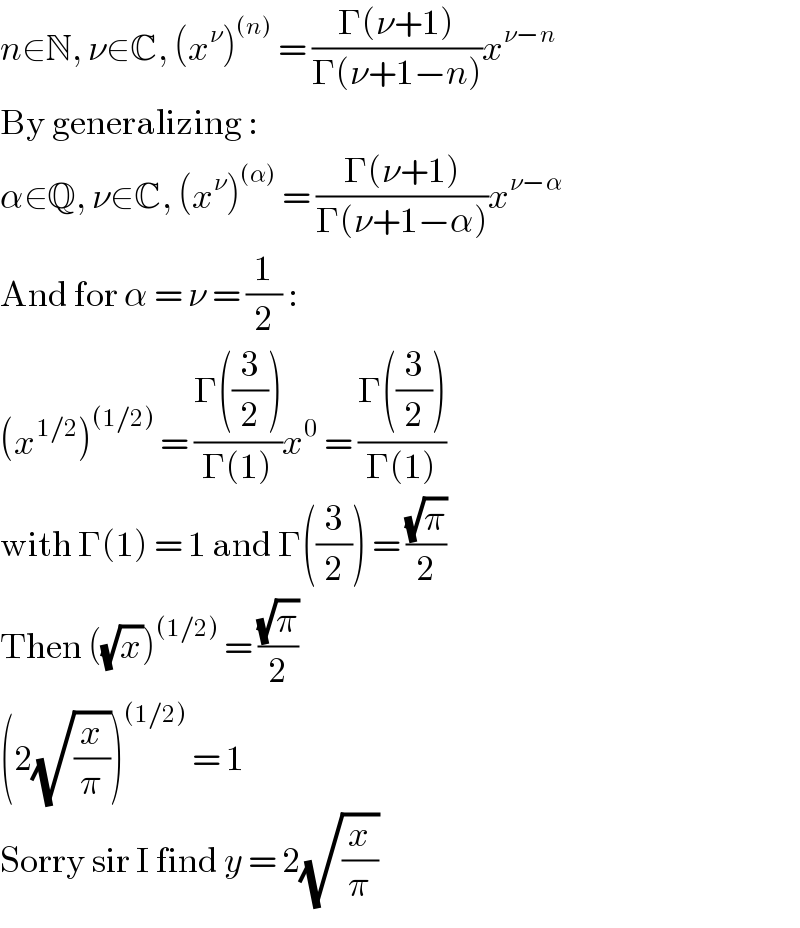
n∈N, ν∈C, (x^ν )^((n)) = ((Γ(ν+1))/(Γ(ν+1−n)))x^(ν−n) By generalizing : α∈Q, ν∈C, (x^ν )^((α)) = ((Γ(ν+1))/(Γ(ν+1−α)))x^(ν−α) And for α = ν = (1/2) : (x^(1/2) )^((1/2)) = ((Γ((3/2)))/(Γ(1)))x^0 = ((Γ((3/2)))/(Γ(1))) with Γ(1) = 1 and Γ((3/2)) = ((√π)/2) Then ((√x))^((1/2)) = ((√π)/2) (2(√(x/π)))^((1/2)) = 1 Sorry sir I find y = 2(√(x/π))
$${n}\in\mathbb{N},\:\nu\in\mathbb{C},\:\left({x}^{\nu} \right)^{\left({n}\right)} \:=\:\frac{\Gamma\left(\nu+\mathrm{1}\right)}{\Gamma\left(\nu+\mathrm{1}−{n}\right)}{x}^{\nu−{n}} \\ $$$$\mathrm{By}\:\mathrm{generalizing}\:: \\ $$$$\alpha\in\mathbb{Q},\:\nu\in\mathbb{C},\:\left({x}^{\nu} \right)^{\left(\alpha\right)} \:=\:\frac{\Gamma\left(\nu+\mathrm{1}\right)}{\Gamma\left(\nu+\mathrm{1}−\alpha\right)}{x}^{\nu−\alpha} \\ $$$$\mathrm{And}\:\mathrm{for}\:\alpha\:=\:\nu\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:: \\ $$$$\left({x}^{\mathrm{1}/\mathrm{2}} \right)^{\left(\mathrm{1}/\mathrm{2}\right)} \:=\:\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{1}\right)}{x}^{\mathrm{0}} \:=\:\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{1}\right)} \\ $$$$\mathrm{with}\:\Gamma\left(\mathrm{1}\right)\:=\:\mathrm{1}\:\mathrm{and}\:\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\:\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$\mathrm{Then}\:\left(\sqrt{{x}}\right)^{\left(\mathrm{1}/\mathrm{2}\right)} \:=\:\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\sqrt{\frac{{x}}{\pi}}\right)^{\left(\mathrm{1}/\mathrm{2}\right)} \:=\:\mathrm{1} \\ $$$$\mathrm{Sorry}\:\mathrm{sir}\:\mathrm{I}\:\mathrm{find}\:{y}\:=\:\mathrm{2}\sqrt{\frac{{x}}{\pi}} \\ $$
Commented by ~blr237~ last updated on 23/Jul/20
yes it′s correct : error of typo But you didn′t prove the proposition only its interplay That generalisation is also correct ( it′s the Caputo derivation) and that coincides with the Riemann-Liouville derivation when α=(1/2) D^α (f)(x)=(1/(Γ(α))) (d/dx)(∫_(0 ) ^x t^(α−1) f(x−t)dt) 0<α D^(1/2) (y)=1⇒D^(1/2) (D^(1/2) (y))=D^(1/2) (1) ⇒ y′(x)= (1/(Γ((1/2)))) (d/dx)( 2(√x) ) ⇒y(x)=2(√(x/π))
$${yes}\:{it}'{s}\:{correct}\::\:{error}\:{of}\:{typo} \\ $$$${But}\:{you}\:{didn}'{t}\:{prove}\:{the}\:{proposition}\:{only}\:{its}\:{interplay}\: \\ $$$${That}\:{generalisation}\:{is}\:{also}\:{correct}\:\left(\:{it}'{s}\:{the}\:{Caputo}\:{derivation}\right)\:{and}\:{that}\:{coincides}\:{with}\:{the}\:{Riemann}-{Liouville}\:{derivation}\:{when}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$${D}^{\alpha} \left({f}\right)\left({x}\right)=\frac{\mathrm{1}}{\Gamma\left(\alpha\right)}\:\frac{{d}}{{dx}}\left(\int_{\mathrm{0}\:} ^{{x}} {t}^{\alpha−\mathrm{1}} {f}\left({x}−{t}\right){dt}\right)\:\:\:\:\:\:\mathrm{0}<\alpha \\ $$$${D}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({y}\right)=\mathrm{1}\Rightarrow{D}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({D}^{\frac{\mathrm{1}}{\mathrm{2}}} \left({y}\right)\right)={D}^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}\right) \\ $$$$\:\:\:\Rightarrow\:{y}'\left({x}\right)=\:\frac{\mathrm{1}}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}\:\frac{{d}}{{dx}}\left(\:\mathrm{2}\sqrt{{x}}\:\right) \\ $$$$\Rightarrow{y}\left({x}\right)=\mathrm{2}\sqrt{\frac{{x}}{\pi}}\:\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *