Menu Close

D-2-2D-1-y-x-ln-x-

Tinku Tara 0 Comments
Pin




Question Number 103201 by bobhans last updated on 13/Jul/20
(D^2 −2D+1)y = x ln(x)
$$\left({D}^{\mathrm{2}} −\mathrm{2}{D}+\mathrm{1}\right){y}\:=\:{x}\:\mathrm{ln}\left({x}\right) \\ $$
Commented by bobhans last updated on 14/Jul/20
thank you both
$${thank}\:{you}\:{both}\: \\ $$
Answered by bramlex last updated on 14/Jul/20
homogenous solution η^2 −2η+1 = 0 ; (η−1)^2 = 0 y_h = C_1 e^x +C_2 xe^x now we use variation of parameters y=u.e^x +v.xe^x differentiating yields y′=u′e^x +ue^x +v′xe^x +v(x+1)e^x setting u′e^x +v′xe^x = 0 y′′ =u′e^x +ue^x +v′(x+1)e^x +v(x+2)e^x substituting y,y′,y′′ into original differential equation gives us (u′e^x +ue^x +v′(x+1)e^x +v(x+2)e^x ) −2(ue^x +v(x+1)e^x )+(ue^x +vxe^x )= xln(x) which simplifies to u′+(x+1)v′=xe^(−x) ln(x) now we have two equations for u′ and v′ ⇒u′e^x +v′xe^x =0 and u′+(x+1)v′ = xe^(−x) ln(x) solving this system of equation u′=−x^2 e^(−x) ln(x) and v′=xe^(−x) ln(x) .integrating gives us u= −∫_1 ^x t^2 e^(−t) ln(t)dt and v = ∫_1 ^x te^(−t) ln(t)dt hence we conclude that a general solution is given by y= C_1 e^x +C_2 xe^x −e^x ∫_1 ^x t^2 e^(−t) ln(t)dt+xe^x ∫_1 ^x te^(−t) ln(t)dt
$$\mathrm{homogenous}\:\mathrm{solution}\: \\ $$$$\eta^{\mathrm{2}} −\mathrm{2}\eta+\mathrm{1}\:=\:\mathrm{0}\:;\:\left(\eta−\mathrm{1}\right)^{\mathrm{2}} =\:\mathrm{0} \\ $$$$\mathrm{y}_{\mathrm{h}} =\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} +\mathrm{C}_{\mathrm{2}} \mathrm{xe}^{\mathrm{x}} \: \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{use}\:\mathrm{variation}\:\mathrm{of} \\ $$$$\mathrm{parameters}\:\mathrm{y}=\mathrm{u}.\mathrm{e}^{\mathrm{x}} \:+\mathrm{v}.\mathrm{xe}^{\mathrm{x}} \\ $$$$\mathrm{differentiating}\:\mathrm{yields} \\ $$$$\mathrm{y}'=\mathrm{u}'\mathrm{e}^{\mathrm{x}} +\mathrm{ue}^{\mathrm{x}} +\mathrm{v}'\mathrm{xe}^{\mathrm{x}} +\mathrm{v}\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \\ $$$$\mathrm{setting}\:\mathrm{u}'\mathrm{e}^{\mathrm{x}} +\mathrm{v}'\mathrm{xe}^{\mathrm{x}} \:=\:\mathrm{0} \\ $$$$\mathrm{y}'' \\ $$$$=\mathrm{u}'\mathrm{e}^{\mathrm{x}} +\mathrm{ue}^{\mathrm{x}} +\mathrm{v}'\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} +\mathrm{v}\left(\mathrm{x}+\mathrm{2}\right)\mathrm{e}^{\mathrm{x}} \\ $$$$\mathrm{substituting}\:\mathrm{y},\mathrm{y}',\mathrm{y}''\:\mathrm{into}\:\mathrm{original} \\ $$$$\mathrm{differential}\:\mathrm{equation}\:\mathrm{gives}\:\mathrm{us} \\ $$$$\left(\mathrm{u}'\mathrm{e}^{\mathrm{x}} +\mathrm{ue}^{\mathrm{x}} +\mathrm{v}'\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} +\mathrm{v}\left(\mathrm{x}+\mathrm{2}\right)\mathrm{e}^{\mathrm{x}} \right) \\ $$$$−\mathrm{2}\left(\mathrm{ue}^{\mathrm{x}} +\mathrm{v}\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \right)+\left(\mathrm{ue}^{\mathrm{x}} +\mathrm{vxe}^{\mathrm{x}} \right)=\:\mathrm{xln}\left(\mathrm{x}\right) \\ $$$$\mathrm{which}\:\mathrm{simplifies}\:\mathrm{to}\: \\ $$$$\mathrm{u}'+\left(\mathrm{x}+\mathrm{1}\right)\mathrm{v}'=\mathrm{xe}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{two}\:\mathrm{equations}\:\mathrm{for} \\ $$$$\mathrm{u}'\:\mathrm{and}\:\mathrm{v}'\:\Rightarrow\mathrm{u}'\mathrm{e}^{\mathrm{x}} +\mathrm{v}'\mathrm{xe}^{\mathrm{x}} =\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{u}'+\left(\mathrm{x}+\mathrm{1}\right)\mathrm{v}'\:=\:\mathrm{xe}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\mathrm{solving}\:\mathrm{this}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equation} \\ $$$$\mathrm{u}'=−\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)\:\mathrm{and} \\ $$$$\mathrm{v}'=\mathrm{xe}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{x}\right)\:.\mathrm{integrating}\:\mathrm{gives} \\ $$$$\mathrm{us}\:\mathrm{u}=\:−\underset{\mathrm{1}} {\overset{\mathrm{x}} {\int}}\mathrm{t}^{\mathrm{2}} \mathrm{e}^{−\mathrm{t}} \mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}\:\mathrm{and}\: \\ $$$$\mathrm{v}\:=\:\underset{\mathrm{1}} {\overset{\mathrm{x}} {\int}}\:\mathrm{te}^{−\mathrm{t}} \:\mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}\: \\ $$$$\mathrm{hence}\:\mathrm{we}\:\mathrm{conclude}\:\mathrm{that}\:\mathrm{a} \\ $$$$\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{given}\:\mathrm{by}\: \\ $$$$\mathrm{y}=\:\mathrm{C}_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} +\mathrm{C}_{\mathrm{2}} \mathrm{xe}^{\mathrm{x}} −\mathrm{e}^{\mathrm{x}} \underset{\mathrm{1}} {\overset{\mathrm{x}} {\int}}\mathrm{t}^{\mathrm{2}} \mathrm{e}^{−\mathrm{t}} \mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}+\mathrm{xe}^{\mathrm{x}} \underset{\mathrm{1}} {\overset{\mathrm{x}} {\int}}\mathrm{te}^{−\mathrm{t}} \mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$ \\ $$
Answered by abdomsup last updated on 13/Jul/20
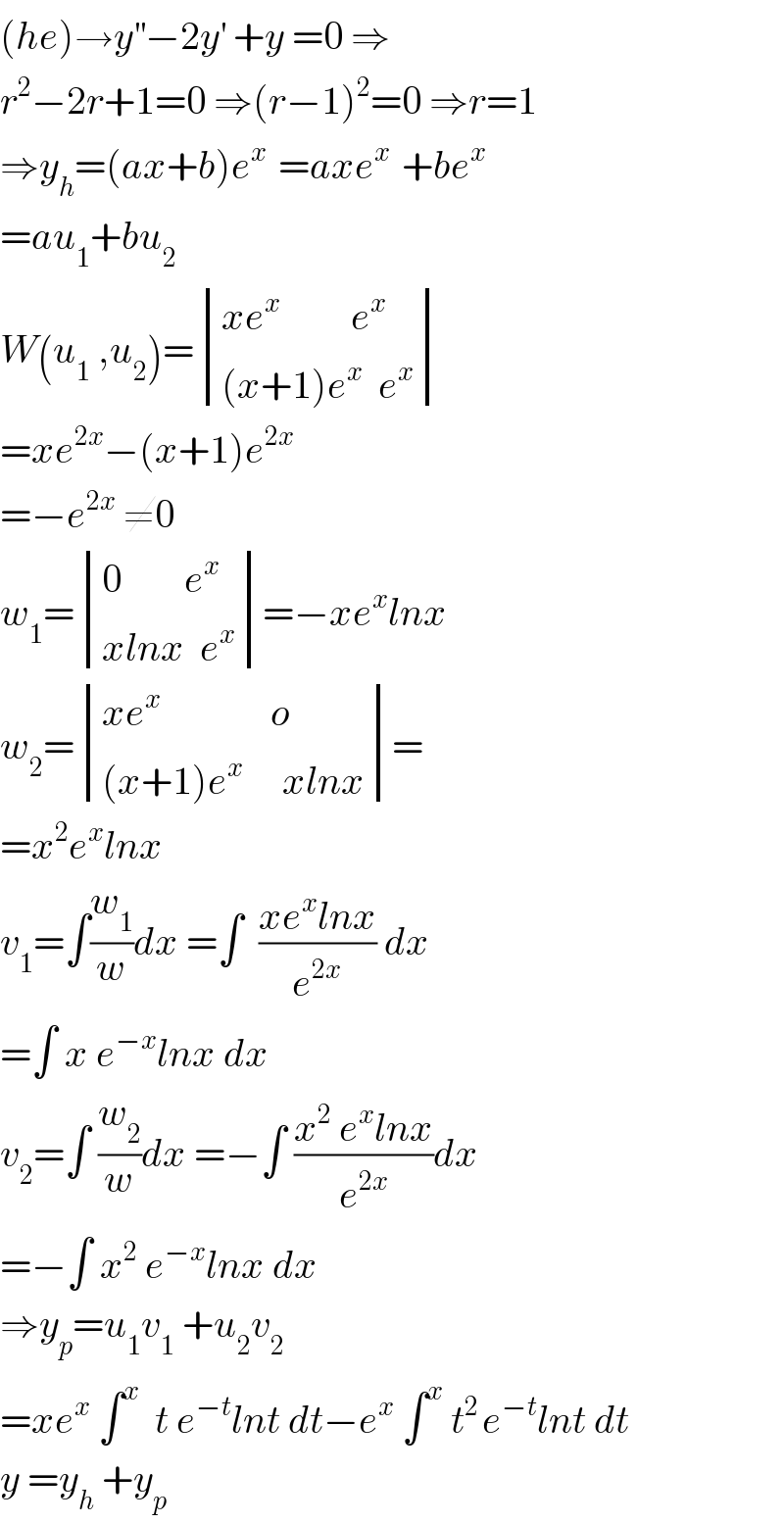
(he)→y^(′′) −2y^′ +y =0 ⇒ r^2 −2r+1=0 ⇒(r−1)^2 =0 ⇒r=1 ⇒y_h =(ax+b)e^(x ) =axe^(x ) +be^x =au_1 +bu_2 W(u_1 ,u_2 )= determinant (((xe^x e^x )),(((x+1)e^x e^x ))) =xe^(2x) −(x+1)e^(2x) =−e^(2x) ≠0 w_1 = determinant (((0 e^x )),((xlnx e^x )))=−xe^x lnx w_2 = determinant (((xe^x o)),(((x+1)e^x xlnx)))= =x^2 e^x lnx v_1 =∫(w_1 /w)dx =∫ ((xe^x lnx)/e^(2x) ) dx =∫ x e^(−x) lnx dx v_2 =∫ (w_2 /w)dx =−∫ ((x^2 e^x lnx)/e^(2x) )dx =−∫ x^2 e^(−x) lnx dx ⇒y_p =u_1 v_1 +u_2 v_2 =xe^x ∫^x t e^(−t) lnt dt−e^x ∫^x t^(2 ) e^(−t) lnt dt y =y_h +y_p
$$\left({he}\right)\rightarrow{y}^{''} −\mathrm{2}{y}^{'} \:+{y}\:=\mathrm{0}\:\Rightarrow \\ $$$${r}^{\mathrm{2}} −\mathrm{2}{r}+\mathrm{1}=\mathrm{0}\:\Rightarrow\left({r}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\:\Rightarrow{r}=\mathrm{1} \\ $$$$\Rightarrow{y}_{{h}} =\left({ax}+{b}\right){e}^{{x}\:} \:={axe}^{{x}\:} \:+{be}^{{x}} \\ $$$$={au}_{\mathrm{1}} +{bu}_{\mathrm{2}} \\ $$$${W}\left({u}_{\mathrm{1}} \:,{u}_{\mathrm{2}} \right)=\begin{vmatrix}{{xe}^{{x}} \:\:\:\:\:\:\:\:\:{e}^{{x}} }\\{\left({x}+\mathrm{1}\right){e}^{{x}} \:\:{e}^{{x}} }\end{vmatrix} \\ $$$$={xe}^{\mathrm{2}{x}} −\left({x}+\mathrm{1}\right){e}^{\mathrm{2}{x}} \\ $$$$=−{e}^{\mathrm{2}{x}} \:\neq\mathrm{0} \\ $$$${w}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:{e}^{{x}} }\\{{xlnx}\:\:{e}^{{x}} }\end{vmatrix}=−{xe}^{{x}} {lnx} \\ $$$${w}_{\mathrm{2}} =\begin{vmatrix}{{xe}^{{x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:{o}}\\{\left({x}+\mathrm{1}\right){e}^{{x}} \:\:\:\:\:{xlnx}}\end{vmatrix}= \\ $$$$={x}^{\mathrm{2}} {e}^{{x}} {lnx} \\ $$$${v}_{\mathrm{1}} =\int\frac{{w}_{\mathrm{1}} }{{w}}{dx}\:=\int\:\:\frac{{xe}^{{x}} {lnx}}{{e}^{\mathrm{2}{x}} }\:{dx} \\ $$$$=\int\:{x}\:{e}^{−{x}} {lnx}\:{dx} \\ $$$${v}_{\mathrm{2}} =\int\:\frac{{w}_{\mathrm{2}} }{{w}}{dx}\:=−\int\:\frac{{x}^{\mathrm{2}} \:{e}^{{x}} {lnx}}{{e}^{\mathrm{2}{x}} }{dx} \\ $$$$=−\int\:{x}^{\mathrm{2}} \:{e}^{−{x}} {lnx}\:{dx} \\ $$$$\Rightarrow{y}_{{p}} ={u}_{\mathrm{1}} {v}_{\mathrm{1}} \:+{u}_{\mathrm{2}} {v}_{\mathrm{2}} \\ $$$$={xe}^{{x}} \:\int^{{x}} \:\:{t}\:{e}^{−{t}} {lnt}\:{dt}−{e}^{{x}} \:\int^{{x}} \:{t}^{\mathrm{2}\:} {e}^{−{t}} {lnt}\:{dt} \\ $$$${y}\:={y}_{{h}} \:+{y}_{{p}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *