Question Number 99989 by bemath last updated on 24/Jun/20
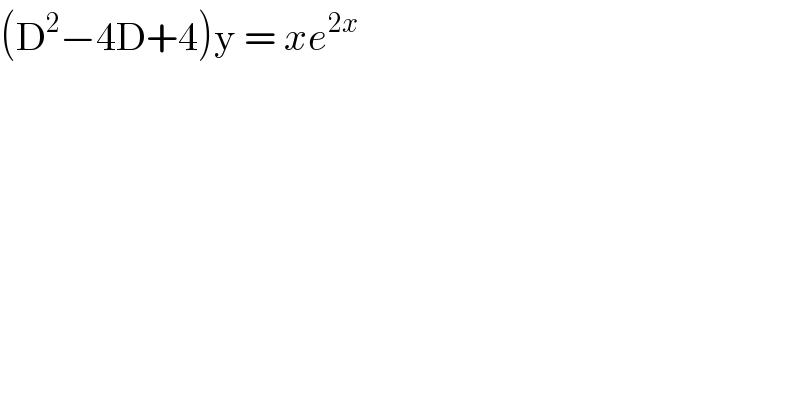
$$\left(\mathrm{D}^{\mathrm{2}} −\mathrm{4D}+\mathrm{4}\right)\mathrm{y}\:=\:{xe}^{\mathrm{2}{x}} \\ $$
Answered by bobhans last updated on 24/Jun/20

$$\mathrm{homogenous}\:\mathrm{solution} \\ $$$$\beta^{\mathrm{2}} −\mathrm{4}\beta+\mathrm{4}=\mathrm{0}\:,\:\mathrm{which}\:\mathrm{has}\:\mathrm{root}\:\beta=\mathrm{2} \\ $$$$\mathrm{hence}\:\mathrm{y}=\:\mathrm{e}^{\mathrm{2x}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{homogenous}\:\mathrm{solution} \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{aplly}\:\mathrm{reduction}\:\mathrm{of}\:\mathrm{order}\:\mathrm{with}\:\mathrm{this} \\ $$$$\mathrm{solution}\:.\:\mathrm{set}\:\mathrm{y}\:=\:\mathrm{e}^{\mathrm{2x}} \:\mathrm{z}\:,\:\mathrm{substituting}\:\mathrm{this} \\ $$$$\mathrm{into}\:\mathrm{the}\:\mathrm{original}\:\mathrm{diff}\:\mathrm{eq}\:\mathrm{yields}\: \\ $$$$\mathrm{e}^{\mathrm{2x}} \left(\mathrm{z}''+\mathrm{4z}'+\mathrm{4z}\right)−\mathrm{4e}^{\mathrm{2x}} \left(\mathrm{z}'+\mathrm{2z}\right)+\mathrm{4e}^{\mathrm{2x}} \:\mathrm{z}\:=\:{xe}^{\mathrm{2}{x}} \\ $$$$\mathrm{which}\:\mathrm{simplifies}\:\mathrm{to}\:\mathrm{z}''\:=\:{x} \\ $$$${integrating}\:{this}\:{twice}\:{in}\:{succession}\:{yields} \\ $$$$\mathrm{z}\:=\:\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{3}} +{C}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} \\ $$$$\mathrm{generall}\:\mathrm{solution}\:\mathrm{y}\:=\:\left(\mathrm{C}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} \right)\mathrm{e}^{\mathrm{2x}} \:+\:\frac{\mathrm{1}}{\mathrm{6}}{x}^{\mathrm{3}} {e}^{\mathrm{2}{x}} \\ $$
Commented by bemath last updated on 24/Jun/20
$$\mathrm{great}…\mathrm{thank}\:\mathrm{much} \\ $$
Answered by mathmax by abdo last updated on 24/Jun/20

$$\mathrm{y}^{''} −\mathrm{4y}^{'} \:+\mathrm{4y}\:=\mathrm{xe}^{\mathrm{2x}} \\ $$$$\left(\mathrm{he}\right)\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{4r}\:+\mathrm{4}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{r}−\mathrm{2}\right)^{\mathrm{2}} \:=\mathrm{0}\Rightarrow\mathrm{r}\:=\mathrm{2}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\left(\mathrm{ax}+\mathrm{b}\right)\mathrm{e}^{\mathrm{2x}} \\ $$$$=\mathrm{axe}^{\mathrm{2x}} \:+\mathrm{be}^{\mathrm{2x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{xe}^{\mathrm{2x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{2x}} \:\:\mathrm{2e}^{\mathrm{2x}} }\end{vmatrix}=\mathrm{2x}\:\mathrm{e}^{\mathrm{4x}} −\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{4x}} \:=−\mathrm{e}^{\mathrm{4x}} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\mathrm{xe}^{\mathrm{2x}} \:\:\:\:\:\mathrm{2e}^{\mathrm{2x}} }\end{vmatrix}=−\mathrm{xe}^{\mathrm{4x}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{xe}^{\mathrm{2x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{2x}} \:\:\:\:\:\mathrm{xe}^{\mathrm{2x}} }\end{vmatrix}=\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{4x}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\:\frac{−\mathrm{xe}^{\mathrm{4x}} }{−\mathrm{e}^{\mathrm{4x}} }\mathrm{dx}\:=\int\:\mathrm{xdx}\:=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{4x}} }{−\mathrm{e}^{\mathrm{4x}} }\mathrm{dx}\:=−\int\:\mathrm{x}^{\mathrm{2}\:} \mathrm{dx}\:=−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}} \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =\mathrm{xe}^{\mathrm{2x}} \left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)+\mathrm{e}^{\mathrm{2x}} \left(−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\right)\:=\left(\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\right)\mathrm{e}^{\mathrm{2x}} \:=\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\:\mathrm{e}^{\mathrm{2x}} \:\Rightarrow \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} =\left(\mathrm{ax}+\mathrm{b}\right)\mathrm{e}^{\mathrm{2x}} \:+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\mathrm{e}^{\mathrm{2x}} \\ $$
