Question Number 103138 by bemath last updated on 13/Jul/20
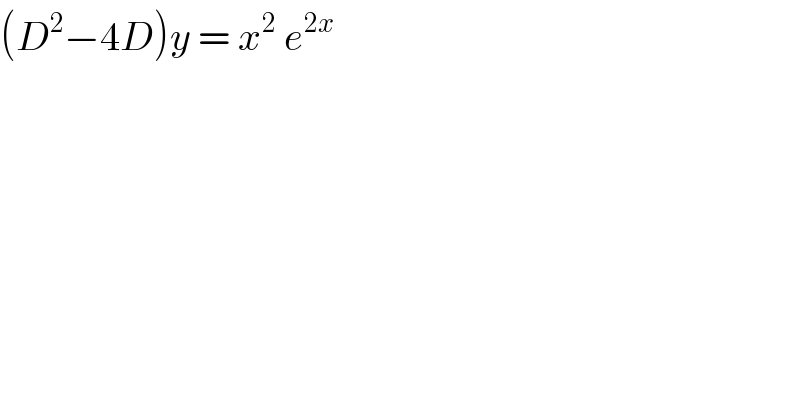
$$\left({D}^{\mathrm{2}} −\mathrm{4}{D}\right){y}\:=\:{x}^{\mathrm{2}} \:{e}^{\mathrm{2}{x}} \\ $$
Commented by bemath last updated on 14/Jul/20
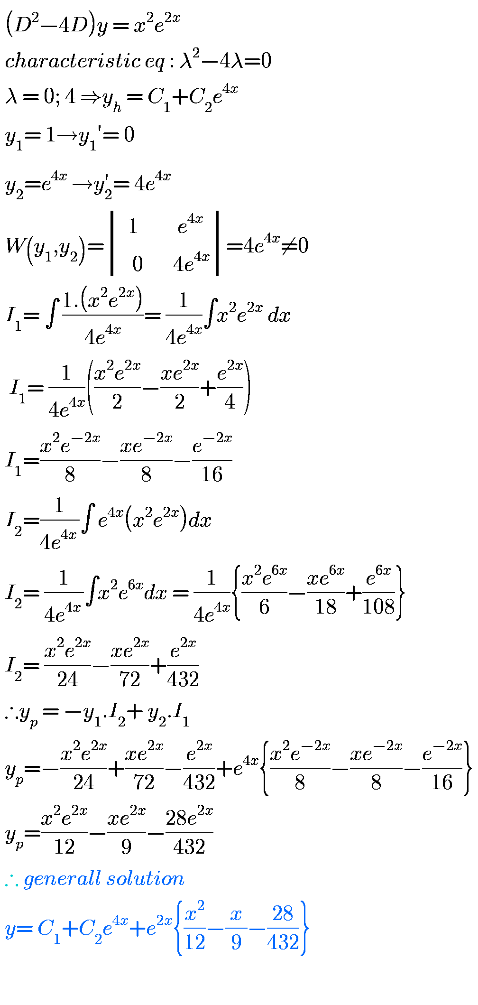
Commented by Israrchajk724 last updated on 13/Jul/20
$$ \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{any}\:\mathrm{one}\:\mathrm{tell}\:\mathrm{me}\:\mathrm{can}\:\mathrm{we}\:\mathrm{convert}\:\mathrm{math}\:\mathrm{editor}\:\mathrm{to}\:\mathrm{word}\:…? \\ $$
Answered by mathmax by abdo last updated on 14/Jul/20
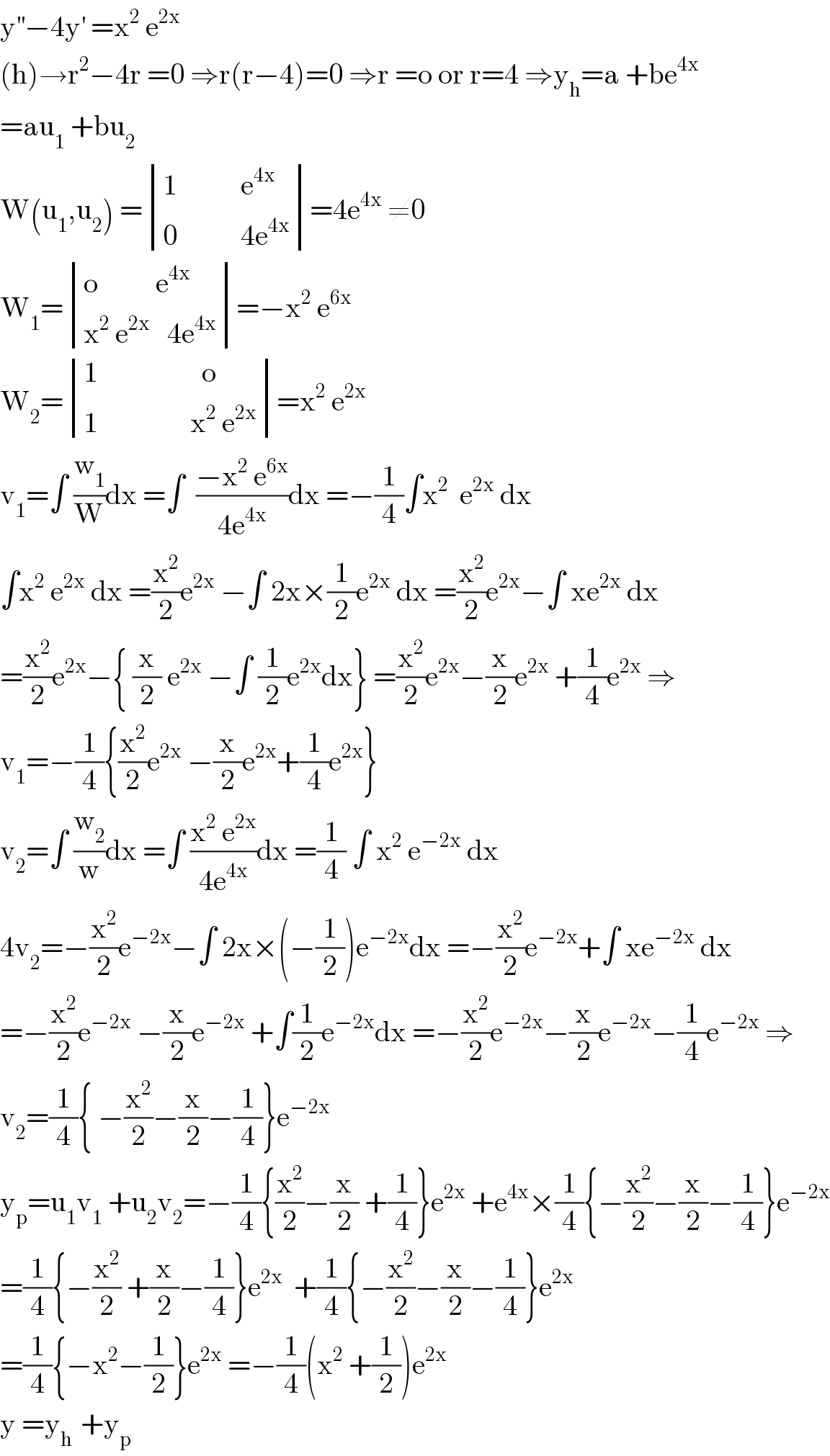
$$\mathrm{y}^{''} −\mathrm{4y}^{'} \:=\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{2x}} \\ $$$$\left(\mathrm{h}\right)\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{4r}\:=\mathrm{0}\:\Rightarrow\mathrm{r}\left(\mathrm{r}−\mathrm{4}\right)=\mathrm{0}\:\Rightarrow\mathrm{r}\:=\mathrm{o}\:\mathrm{or}\:\mathrm{r}=\mathrm{4}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{a}\:+\mathrm{be}^{\mathrm{4x}} \\ $$$$=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{4x}} }\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\mathrm{4e}^{\mathrm{4x}} }\end{vmatrix}=\mathrm{4e}^{\mathrm{4x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{4x}} }\\{\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{2x}} \:\:\:\mathrm{4e}^{\mathrm{4x}} }\end{vmatrix}=−\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{6x}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{o}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{2x}} }\end{vmatrix}=\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{2x}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{−\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{6x}} }{\mathrm{4e}^{\mathrm{4x}} }\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{4}}\int\mathrm{x}^{\mathrm{2}} \:\:\mathrm{e}^{\mathrm{2x}} \:\mathrm{dx} \\ $$$$\int\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{2x}} \:\mathrm{dx}\:=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \:−\int\:\mathrm{2x}×\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \:\mathrm{dx}\:=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} −\int\:\mathrm{xe}^{\mathrm{2x}} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} −\left\{\:\frac{\mathrm{x}}{\mathrm{2}}\:\mathrm{e}^{\mathrm{2x}} \:−\int\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \mathrm{dx}\right\}\:=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} −\frac{\mathrm{x}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{\mathrm{2x}} \:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{4}}\left\{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \:−\frac{\mathrm{x}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} +\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{\mathrm{2x}} \right\} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{2x}} }{\mathrm{4e}^{\mathrm{4x}} }\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx} \\ $$$$\mathrm{4v}_{\mathrm{2}} =−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} −\int\:\mathrm{2x}×\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{e}^{−\mathrm{2x}} \mathrm{dx}\:=−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} +\int\:\mathrm{xe}^{−\mathrm{2x}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} \:−\frac{\mathrm{x}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} \:+\int\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} \mathrm{dx}\:=−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} −\frac{\mathrm{x}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} −\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\mathrm{2x}} \:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\left\{\:−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right\}\mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{4}}\left\{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}\right\}\mathrm{e}^{\mathrm{2x}} \:+\mathrm{e}^{\mathrm{4x}} ×\frac{\mathrm{1}}{\mathrm{4}}\left\{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right\}\mathrm{e}^{−\mathrm{2x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right\}\mathrm{e}^{\mathrm{2x}} \:\:+\frac{\mathrm{1}}{\mathrm{4}}\left\{−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\right\}\mathrm{e}^{\mathrm{2x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left\{−\mathrm{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\right\}\mathrm{e}^{\mathrm{2x}} \:=−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{e}^{\mathrm{2x}} \\ $$$$\mathrm{y}\:=\mathrm{y}_{\mathrm{h}\:} \:+\mathrm{y}_{\mathrm{p}} \\ $$
