Menu Close

d-2-9-2-

Tinku Tara 0 Comments
Pin




Question Number 118905 by benjo_mathlover last updated on 20/Oct/20
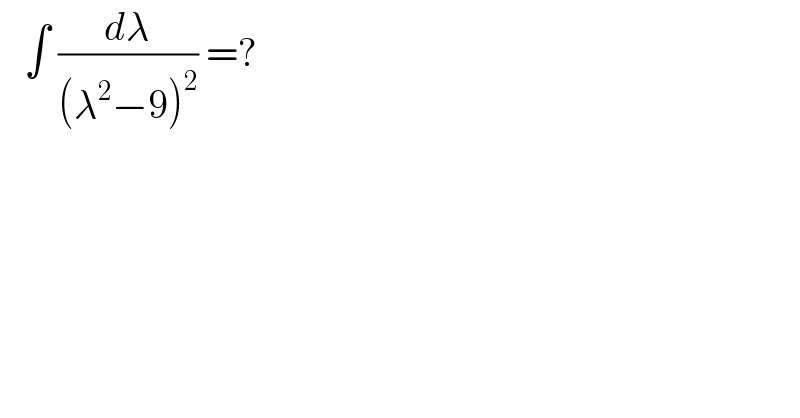
∫ (dλ/((λ^2 −9)^2 )) =?
$$\:\:\:\int\:\frac{{d}\lambda}{\left(\lambda^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{2}} }\:=?\: \\ $$
Answered by Bird last updated on 21/Oct/20
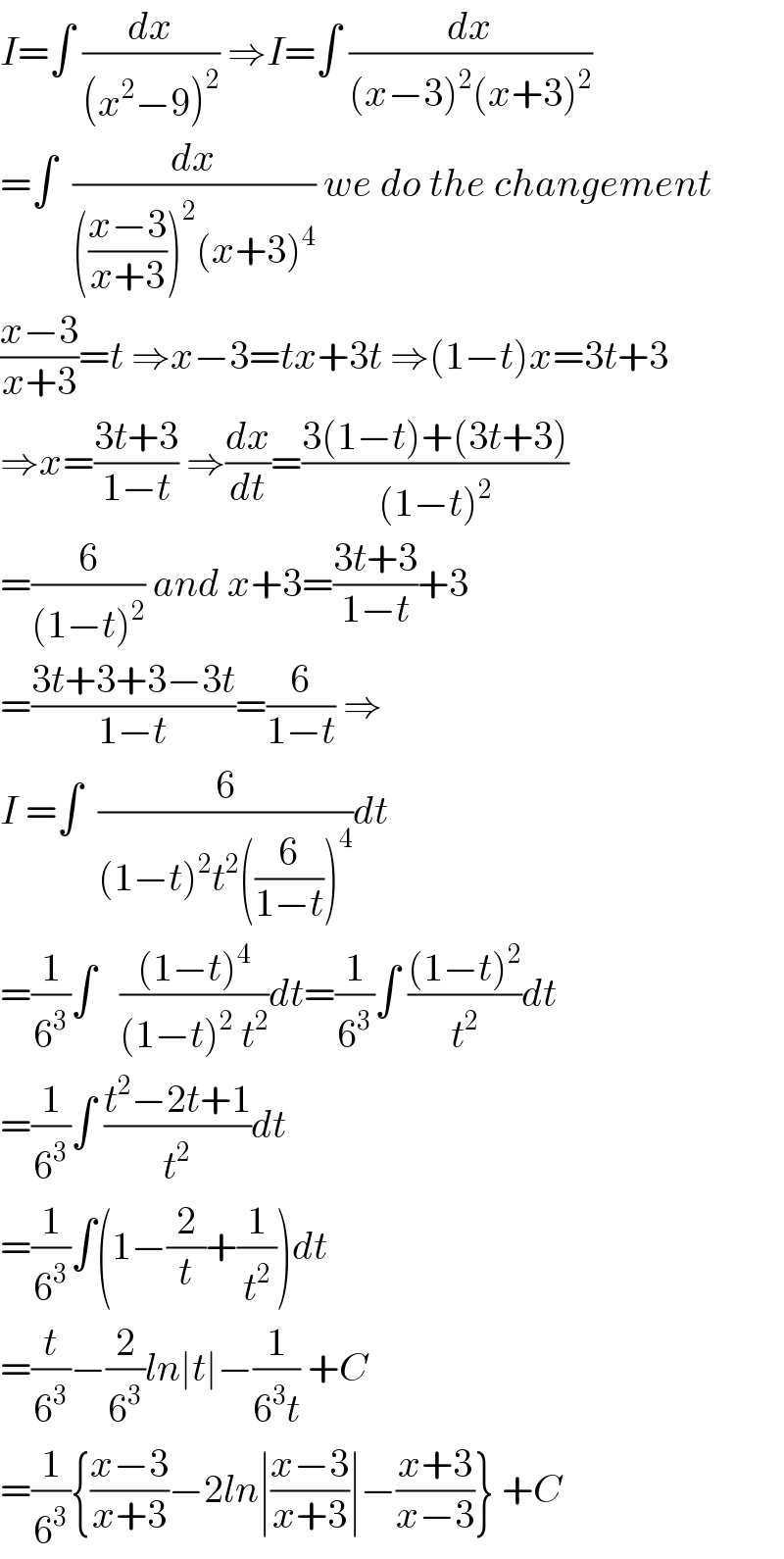
I=∫ (dx/((x^2 −9)^2 )) ⇒I=∫ (dx/((x−3)^2 (x+3)^2 )) =∫ (dx/((((x−3)/(x+3)))^2 (x+3)^4 )) we do the changement ((x−3)/(x+3))=t ⇒x−3=tx+3t ⇒(1−t)x=3t+3 ⇒x=((3t+3)/(1−t)) ⇒(dx/dt)=((3(1−t)+(3t+3))/((1−t)^2 )) =(6/((1−t)^2 )) and x+3=((3t+3)/(1−t))+3 =((3t+3+3−3t)/(1−t))=(6/(1−t)) ⇒ I =∫ (6/((1−t)^2 t^2 ((6/(1−t)))^4 ))dt =(1/6^3 )∫ (((1−t)^4 )/((1−t)^2 t^2 ))dt=(1/6^3 )∫ (((1−t)^2 )/t^2 )dt =(1/6^3 )∫ ((t^2 −2t+1)/t^2 )dt =(1/6^3 )∫(1−(2/t)+(1/t^2 ))dt =(t/6^3 )−(2/6^3 )ln∣t∣−(1/(6^3 t)) +C =(1/6^3 ){((x−3)/(x+3))−2ln∣((x−3)/(x+3))∣−((x+3)/(x−3))} +C
$${I}=\int\:\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{2}} }\:\Rightarrow{I}=\int\:\frac{{dx}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} \left({x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$=\int\:\:\frac{{dx}}{\left(\frac{{x}−\mathrm{3}}{{x}+\mathrm{3}}\right)^{\mathrm{2}} \left({x}+\mathrm{3}\right)^{\mathrm{4}} }\:{we}\:{do}\:{the}\:{changement} \\ $$$$\frac{{x}−\mathrm{3}}{{x}+\mathrm{3}}={t}\:\Rightarrow{x}−\mathrm{3}={tx}+\mathrm{3}{t}\:\Rightarrow\left(\mathrm{1}−{t}\right){x}=\mathrm{3}{t}+\mathrm{3} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}{t}+\mathrm{3}}{\mathrm{1}−{t}}\:\Rightarrow\frac{{dx}}{{dt}}=\frac{\mathrm{3}\left(\mathrm{1}−{t}\right)+\left(\mathrm{3}{t}+\mathrm{3}\right)}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{6}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }\:{and}\:{x}+\mathrm{3}=\frac{\mathrm{3}{t}+\mathrm{3}}{\mathrm{1}−{t}}+\mathrm{3} \\ $$$$=\frac{\mathrm{3}{t}+\mathrm{3}+\mathrm{3}−\mathrm{3}{t}}{\mathrm{1}−{t}}=\frac{\mathrm{6}}{\mathrm{1}−{t}}\:\Rightarrow \\ $$$${I}\:=\int\:\:\frac{\mathrm{6}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} {t}^{\mathrm{2}} \left(\frac{\mathrm{6}}{\mathrm{1}−{t}}\right)^{\mathrm{4}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{3}} }\int\:\:\:\frac{\left(\mathrm{1}−{t}\right)^{\mathrm{4}} }{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} \:{t}^{\mathrm{2}} }{dt}=\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{3}} }\int\:\frac{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{3}} }\int\:\frac{{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{3}} }\int\left(\mathrm{1}−\frac{\mathrm{2}}{{t}}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){dt} \\ $$$$=\frac{{t}}{\mathrm{6}^{\mathrm{3}} }−\frac{\mathrm{2}}{\mathrm{6}^{\mathrm{3}} }{ln}\mid{t}\mid−\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{3}} {t}}\:+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{3}} }\left\{\frac{{x}−\mathrm{3}}{{x}+\mathrm{3}}−\mathrm{2}{ln}\mid\frac{{x}−\mathrm{3}}{{x}+\mathrm{3}}\mid−\frac{{x}+\mathrm{3}}{{x}−\mathrm{3}}\right\}\:+{C} \\ $$
Answered by MJS_new last updated on 20/Oct/20
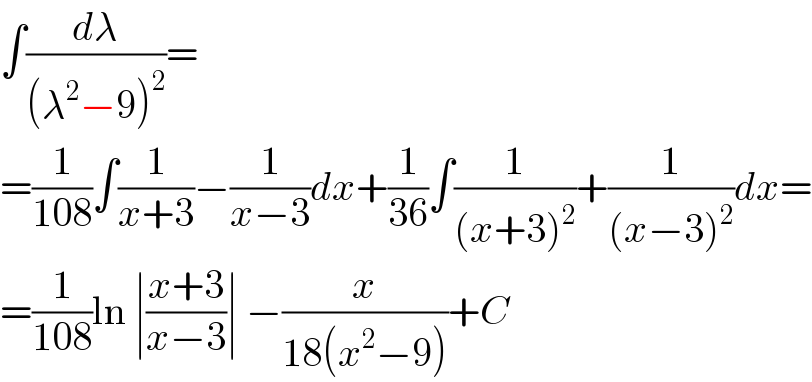
∫(dλ/((λ^2 −9)^2 ))= =(1/(108))∫(1/(x+3))−(1/(x−3))dx+(1/(36))∫(1/((x+3)^2 ))+(1/((x−3)^2 ))dx= =(1/(108))ln ∣((x+3)/(x−3))∣ −(x/(18(x^2 −9)))+C
$$\int\frac{{d}\lambda}{\left(\lambda^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{1}}{\mathrm{108}}\int\frac{\mathrm{1}}{{x}+\mathrm{3}}−\frac{\mathrm{1}}{{x}−\mathrm{3}}{dx}+\frac{\mathrm{1}}{\mathrm{36}}\int\frac{\mathrm{1}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({x}−\mathrm{3}\right)^{\mathrm{2}} }{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{108}}\mathrm{ln}\:\mid\frac{{x}+\mathrm{3}}{{x}−\mathrm{3}}\mid\:−\frac{{x}}{\mathrm{18}\left({x}^{\mathrm{2}} −\mathrm{9}\right)}+{C} \\ $$
Commented by Dwaipayan Shikari last updated on 20/Oct/20
Typo ∫(dλ/((λ^2 −9)^2 ))
$${Typo} \\ $$$$\int\frac{{d}\lambda}{\left(\lambda^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{2}} } \\ $$
Commented by MJS_new last updated on 20/Oct/20
I′m the Master of Typos it seems... thank you!
$$\mathrm{I}'\mathrm{m}\:\mathrm{the}\:\mathrm{Master}\:\mathrm{of}\:\mathrm{Typos}\:\mathrm{it}\:\mathrm{seems}…\:\mathrm{thank}\:\mathrm{you}! \\ $$
Commented by Dwaipayan Shikari last updated on 20/Oct/20
You are getting old sir! :) So it happens:)
$$\left.\:\left.{You}\:{are}\:{getting}\:{old}\:{sir}!\:\::\right)\:{So}\:{it}\:{happens}:\right) \\ $$
Commented by MJS_new last updated on 20/Oct/20
I got used to getting older from my first breath...
$$\mathrm{I}\:\mathrm{got}\:\mathrm{used}\:\mathrm{to}\:\mathrm{getting}\:\mathrm{older}\:\mathrm{from}\:\mathrm{my}\:\mathrm{first} \\ $$$$\mathrm{breath}… \\ $$
Answered by Dwaipayan Shikari last updated on 20/Oct/20
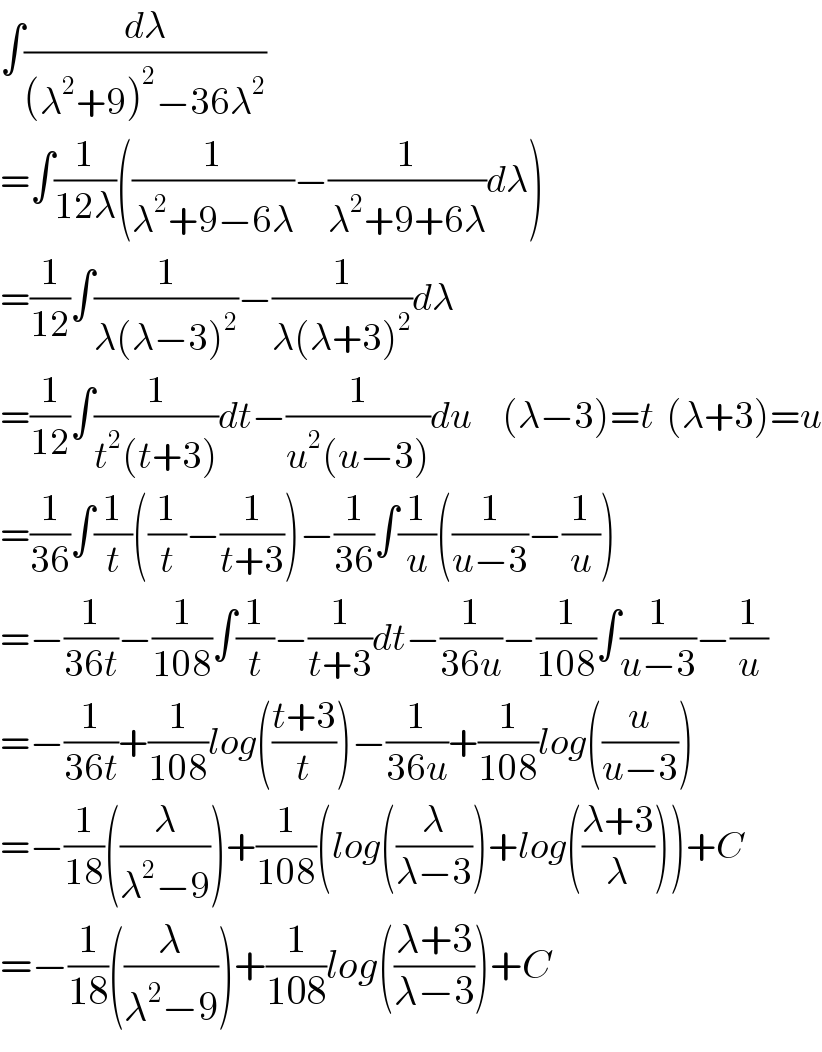
∫(dλ/((λ^2 +9)^2 −36λ^2 )) =∫(1/(12λ))((1/(λ^2 +9−6λ))−(1/(λ^2 +9+6λ))dλ) =(1/(12))∫(1/(λ(λ−3)^2 ))−(1/(λ(λ+3)^2 ))dλ =(1/(12))∫(1/(t^2 (t+3)))dt−(1/(u^2 (u−3)))du (λ−3)=t (λ+3)=u =(1/(36))∫(1/t)((1/t)−(1/(t+3)))−(1/(36))∫(1/u)((1/(u−3))−(1/u)) =−(1/(36t))−(1/(108))∫(1/t)−(1/(t+3))dt−(1/(36u))−(1/(108))∫(1/(u−3))−(1/u) =−(1/(36t))+(1/(108))log(((t+3)/t))−(1/(36u))+(1/(108))log((u/(u−3))) =−(1/(18))((λ/(λ^2 −9)))+(1/(108))(log((λ/(λ−3)))+log(((λ+3)/λ)))+C =−(1/(18))((λ/(λ^2 −9)))+(1/(108))log(((λ+3)/(λ−3)))+C
$$\int\frac{{d}\lambda}{\left(\lambda^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{2}} −\mathrm{36}\lambda^{\mathrm{2}} } \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{12}\lambda}\left(\frac{\mathrm{1}}{\lambda^{\mathrm{2}} +\mathrm{9}−\mathrm{6}\lambda}−\frac{\mathrm{1}}{\lambda^{\mathrm{2}} +\mathrm{9}+\mathrm{6}\lambda}{d}\lambda\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\int\frac{\mathrm{1}}{\lambda\left(\lambda−\mathrm{3}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\lambda\left(\lambda+\mathrm{3}\right)^{\mathrm{2}} }{d}\lambda\:\:\:\:\:\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} \left({t}+\mathrm{3}\right)}{dt}−\frac{\mathrm{1}}{{u}^{\mathrm{2}} \left({u}−\mathrm{3}\right)}{du}\:\:\:\:\:\left(\lambda−\mathrm{3}\right)={t}\:\:\left(\lambda+\mathrm{3}\right)={u} \\ $$$$=\frac{\mathrm{1}}{\mathrm{36}}\int\frac{\mathrm{1}}{{t}}\left(\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{{t}+\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{36}}\int\frac{\mathrm{1}}{{u}}\left(\frac{\mathrm{1}}{{u}−\mathrm{3}}−\frac{\mathrm{1}}{{u}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{36}{t}}−\frac{\mathrm{1}}{\mathrm{108}}\int\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{{t}+\mathrm{3}}{dt}−\frac{\mathrm{1}}{\mathrm{36}{u}}−\frac{\mathrm{1}}{\mathrm{108}}\int\frac{\mathrm{1}}{{u}−\mathrm{3}}−\frac{\mathrm{1}}{{u}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{36}{t}}+\frac{\mathrm{1}}{\mathrm{108}}{log}\left(\frac{{t}+\mathrm{3}}{{t}}\right)−\frac{\mathrm{1}}{\mathrm{36}{u}}+\frac{\mathrm{1}}{\mathrm{108}}{log}\left(\frac{{u}}{{u}−\mathrm{3}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{18}}\left(\frac{\lambda}{\lambda^{\mathrm{2}} −\mathrm{9}}\right)+\frac{\mathrm{1}}{\mathrm{108}}\left({log}\left(\frac{\lambda}{\lambda−\mathrm{3}}\right)+{log}\left(\frac{\lambda+\mathrm{3}}{\lambda}\right)\right)+{C} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{18}}\left(\frac{\lambda}{\lambda^{\mathrm{2}} −\mathrm{9}}\right)+\frac{\mathrm{1}}{\mathrm{108}}{log}\left(\frac{\lambda+\mathrm{3}}{\lambda−\mathrm{3}}\right)+{C} \\ $$
Answered by bramlexs22 last updated on 20/Oct/20
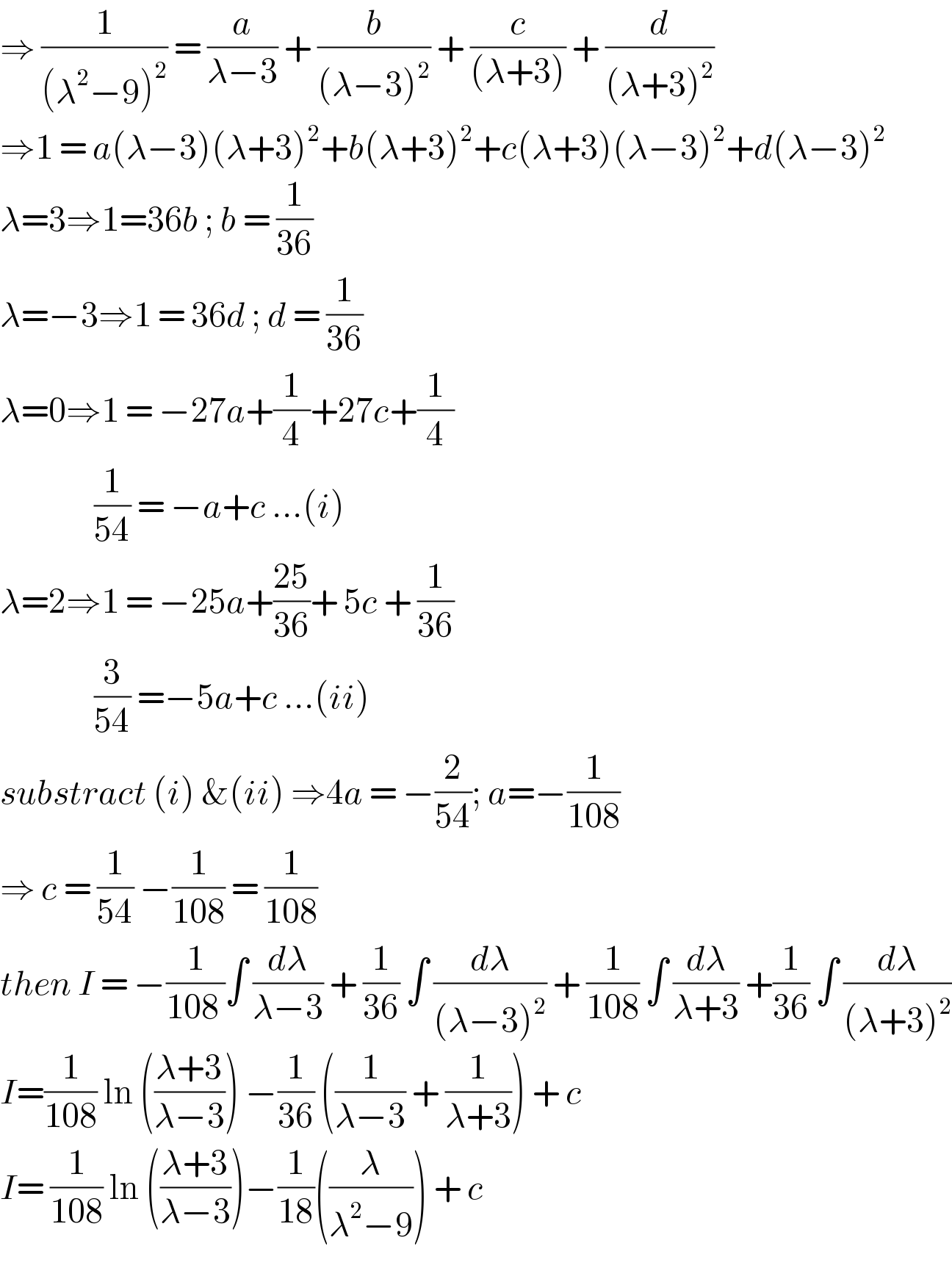
⇒ (1/((λ^2 −9)^2 )) = (a/(λ−3)) + (b/((λ−3)^2 )) + (c/((λ+3))) + (d/((λ+3)^2 )) ⇒1 = a(λ−3)(λ+3)^2 +b(λ+3)^2 +c(λ+3)(λ−3)^2 +d(λ−3)^2 λ=3⇒1=36b ; b = (1/(36)) λ=−3⇒1 = 36d ; d = (1/(36)) λ=0⇒1 = −27a+(1/4)+27c+(1/4) (1/(54)) = −a+c ...(i) λ=2⇒1 = −25a+((25)/(36))+ 5c + (1/(36)) (3/(54)) =−5a+c ...(ii) substract (i) &(ii) ⇒4a = −(2/(54)); a=−(1/(108)) ⇒ c = (1/(54)) −(1/(108)) = (1/(108)) then I = −(1/(108 ))∫ (dλ/(λ−3)) + (1/(36)) ∫ (dλ/((λ−3)^2 )) + (1/(108)) ∫ (dλ/(λ+3)) +(1/(36)) ∫ (dλ/((λ+3)^2 )) I=(1/(108)) ln (((λ+3)/(λ−3))) −(1/(36)) ((1/(λ−3)) + (1/(λ+3))) + c I= (1/(108)) ln (((λ+3)/(λ−3)))−(1/(18))((λ/(λ^2 −9))) + c
$$\Rightarrow\:\frac{\mathrm{1}}{\left(\lambda^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{2}} }\:=\:\frac{{a}}{\lambda−\mathrm{3}}\:+\:\frac{{b}}{\left(\lambda−\mathrm{3}\right)^{\mathrm{2}} }\:+\:\frac{{c}}{\left(\lambda+\mathrm{3}\right)}\:+\:\frac{{d}}{\left(\lambda+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{1}\:=\:{a}\left(\lambda−\mathrm{3}\right)\left(\lambda+\mathrm{3}\right)^{\mathrm{2}} +{b}\left(\lambda+\mathrm{3}\right)^{\mathrm{2}} +{c}\left(\lambda+\mathrm{3}\right)\left(\lambda−\mathrm{3}\right)^{\mathrm{2}} +{d}\left(\lambda−\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\lambda=\mathrm{3}\Rightarrow\mathrm{1}=\mathrm{36}{b}\:;\:{b}\:=\:\frac{\mathrm{1}}{\mathrm{36}} \\ $$$$\lambda=−\mathrm{3}\Rightarrow\mathrm{1}\:=\:\mathrm{36}{d}\:;\:{d}\:=\:\frac{\mathrm{1}}{\mathrm{36}} \\ $$$$\lambda=\mathrm{0}\Rightarrow\mathrm{1}\:=\:−\mathrm{27}{a}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{27}{c}+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{54}}\:=\:−{a}+{c}\:…\left({i}\right) \\ $$$$\lambda=\mathrm{2}\Rightarrow\mathrm{1}\:=\:−\mathrm{25}{a}+\frac{\mathrm{25}}{\mathrm{36}}+\:\mathrm{5}{c}\:+\:\frac{\mathrm{1}}{\mathrm{36}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{3}}{\mathrm{54}}\:=−\mathrm{5}{a}+{c}\:…\left({ii}\right) \\ $$$${substract}\:\left({i}\right)\:\&\left({ii}\right)\:\Rightarrow\mathrm{4}{a}\:=\:−\frac{\mathrm{2}}{\mathrm{54}};\:{a}=−\frac{\mathrm{1}}{\mathrm{108}} \\ $$$$\Rightarrow\:{c}\:=\:\frac{\mathrm{1}}{\mathrm{54}}\:−\frac{\mathrm{1}}{\mathrm{108}}\:=\:\frac{\mathrm{1}}{\mathrm{108}} \\ $$$${then}\:{I}\:=\:−\frac{\mathrm{1}}{\mathrm{108}\:}\int\:\frac{{d}\lambda}{\lambda−\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{36}}\:\int\:\frac{{d}\lambda}{\left(\lambda−\mathrm{3}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{108}}\:\int\:\frac{{d}\lambda}{\lambda+\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{36}}\:\int\:\frac{{d}\lambda}{\left(\lambda+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{108}}\:\mathrm{ln}\:\left(\frac{\lambda+\mathrm{3}}{\lambda−\mathrm{3}}\right)\:−\frac{\mathrm{1}}{\mathrm{36}}\:\left(\frac{\mathrm{1}}{\lambda−\mathrm{3}}\:+\:\frac{\mathrm{1}}{\lambda+\mathrm{3}}\right)\:+\:{c} \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{108}}\:\mathrm{ln}\:\left(\frac{\lambda+\mathrm{3}}{\lambda−\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{18}}\left(\frac{\lambda}{\lambda^{\mathrm{2}} −\mathrm{9}}\right)\:+\:{c}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *