d-2-dt-2-g-l-sin-0-Or-t-g-l-t-0-

Question Number 114340 by Dwaipayan Shikari last updated on 18/Sep/20

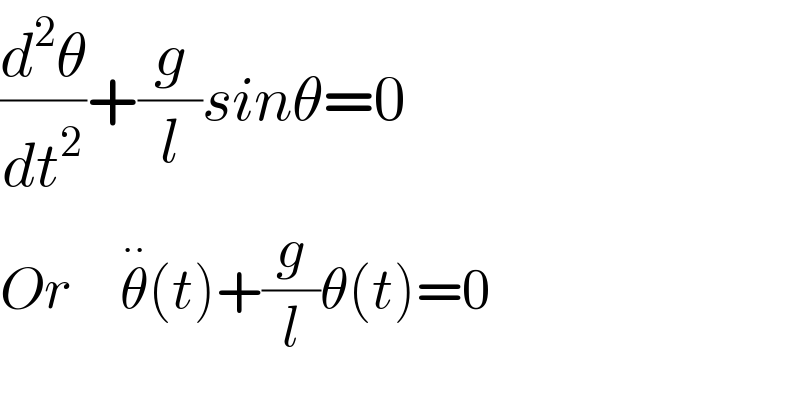
(d^2 θ/dt^2 )+(g/l)sinθ=0 Or θ^(∙∙) (t)+(g/l)θ(t)=0

$$\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }+\frac{{g}}{{l}}{sin}\theta=\mathrm{0} \\ $$$${Or}\:\:\:\:\:\overset{\centerdot\centerdot} {\theta}\left({t}\right)+\frac{{g}}{{l}}\theta\left({t}\right)=\mathrm{0} \\ $$

Commented by mr W last updated on 18/Sep/20

Commented by mohammad17 last updated on 18/Sep/20

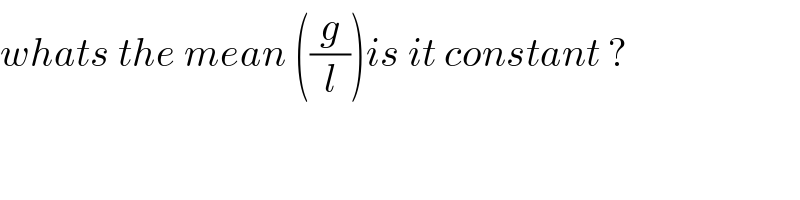
$${whats}\:{the}\:{mean}\:\left(\frac{{g}}{{l}}\right){is}\:{it}\:{constant}\:? \\ $$

Commented by Dwaipayan Shikari last updated on 18/Sep/20

Commented by Dwaipayan Shikari last updated on 18/Sep/20

Gravitational accelaration on simple pendulam (−g) On horizontal direction −gsinθ S=lθ (d^2 s/dt^2 )=l(d^2 θ/dt^2 ) l(d^2 θ/dt^2 )=−gsinθ (d^2 θ/dt^2 )+(g/l)sinθ=0

$${Gravitational}\:{accelaration}\:{on}\:{simple}\:{pendulam}\:\:\left(−{g}\right) \\ $$$${On}\:{horizontal}\:{direction}\:\:−{gsin}\theta \\ $$$${S}={l}\theta \\ $$$$\frac{{d}^{\mathrm{2}} {s}}{{dt}^{\mathrm{2}} }={l}\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} } \\ $$$${l}\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }=−{gsin}\theta \\ $$$$\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }+\frac{{g}}{{l}}{sin}\theta=\mathrm{0} \\ $$$$ \\ $$

Answered by Rio Michael last updated on 18/Sep/20

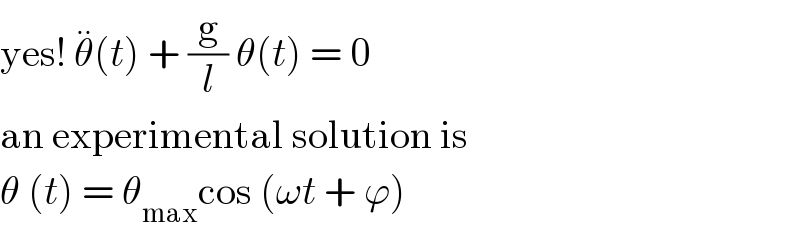
yes! θ^(..) (t) + (g/l) θ(t) = 0 an experimental solution is θ (t) = θ_(max) cos (ωt + ϕ)

$$\mathrm{yes}!\:\overset{..} {\theta}\left({t}\right)\:+\:\frac{\mathrm{g}}{{l}}\:\theta\left({t}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{an}\:\mathrm{experimental}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\theta\:\left({t}\right)\:=\:\theta_{\mathrm{max}} \mathrm{cos}\:\left(\omega{t}\:+\:\varphi\right)\: \\ $$

Facebook Tweet Pin

d-2-dt-2-g-l-sin-0-Or-t-g-l-t-0-

Leave a Reply Cancel reply