Question Number 116052 by Study last updated on 30/Sep/20
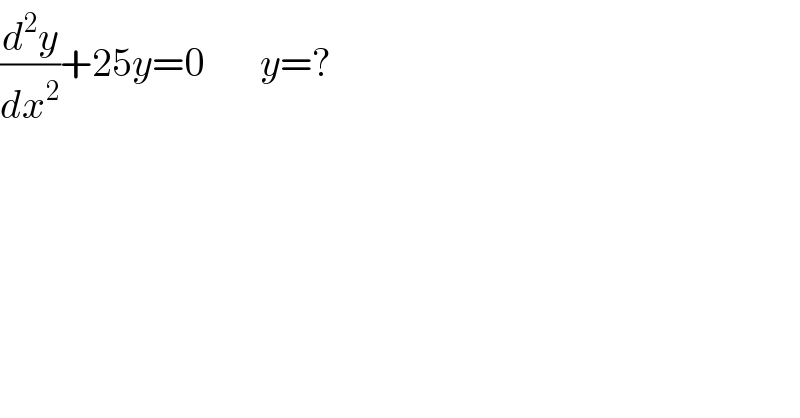
$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{25}{y}=\mathrm{0}\:\:\:\:\:\:\:{y}=? \\ $$
Commented by mohammad17 last updated on 30/Sep/20
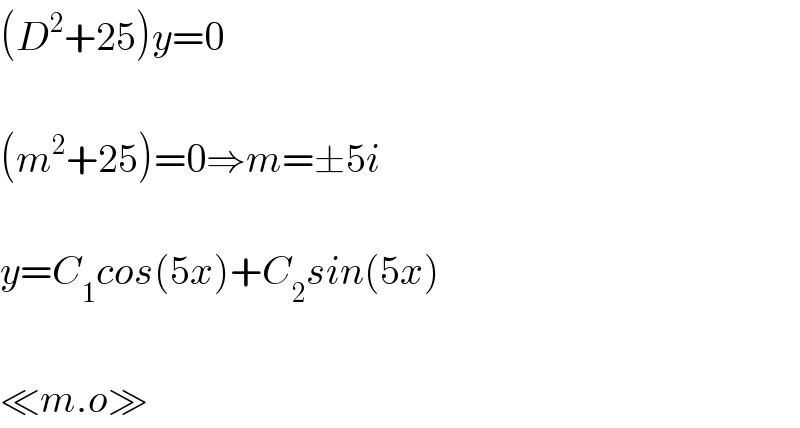
$$\left({D}^{\mathrm{2}} +\mathrm{25}\right){y}=\mathrm{0} \\ $$$$ \\ $$$$\left({m}^{\mathrm{2}} +\mathrm{25}\right)=\mathrm{0}\Rightarrow{m}=\pm\mathrm{5}{i} \\ $$$$ \\ $$$${y}={C}_{\mathrm{1}} {cos}\left(\mathrm{5}{x}\right)+{C}_{\mathrm{2}} {sin}\left(\mathrm{5}{x}\right) \\ $$$$ \\ $$$$\ll{m}.{o}\gg \\ $$
Answered by Dwaipayan Shikari last updated on 30/Sep/20
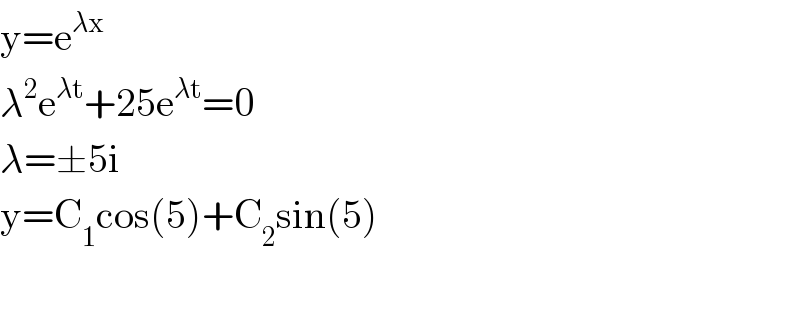
$$\mathrm{y}=\mathrm{e}^{\lambda\mathrm{x}} \\ $$$$\lambda^{\mathrm{2}} \mathrm{e}^{\lambda\mathrm{t}} +\mathrm{25e}^{\lambda\mathrm{t}} =\mathrm{0} \\ $$$$\lambda=\pm\mathrm{5i} \\ $$$$\mathrm{y}=\mathrm{C}_{\mathrm{1}} \mathrm{cos}\left(\mathrm{5}\right)+\mathrm{C}_{\mathrm{2}} \mathrm{sin}\left(\mathrm{5}\right) \\ $$$$ \\ $$
Answered by Bird last updated on 30/Sep/20
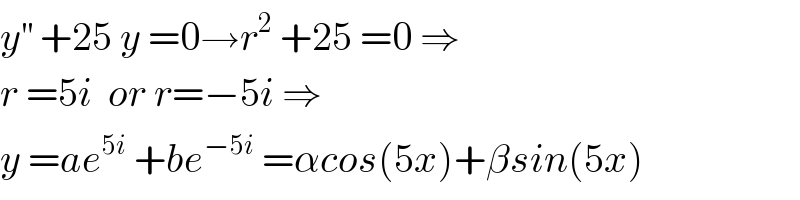
$${y}^{''} \:+\mathrm{25}\:{y}\:=\mathrm{0}\rightarrow{r}^{\mathrm{2}} \:+\mathrm{25}\:=\mathrm{0}\:\Rightarrow \\ $$$${r}\:=\mathrm{5}{i}\:\:{or}\:{r}=−\mathrm{5}{i}\:\Rightarrow \\ $$$${y}\:={ae}^{\mathrm{5}{i}} \:+{be}^{−\mathrm{5}{i}} \:=\alpha{cos}\left(\mathrm{5}{x}\right)+\beta{sin}\left(\mathrm{5}{x}\right) \\ $$
Commented by Bird last updated on 30/Sep/20
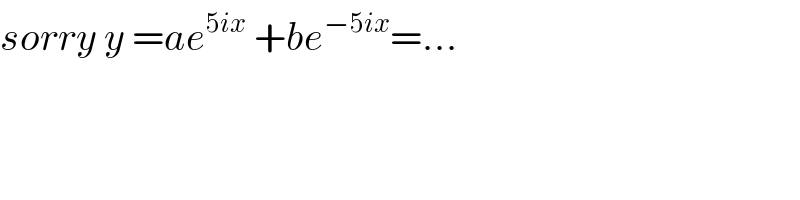
$${sorry}\:{y}\:={ae}^{\mathrm{5}{ix}} \:+{be}^{−\mathrm{5}{ix}} =… \\ $$
