Menu Close

d-2-y-dx-2-3-dy-dx-4y-tan-x-log-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 162338 by HongKing last updated on 28/Dec/21
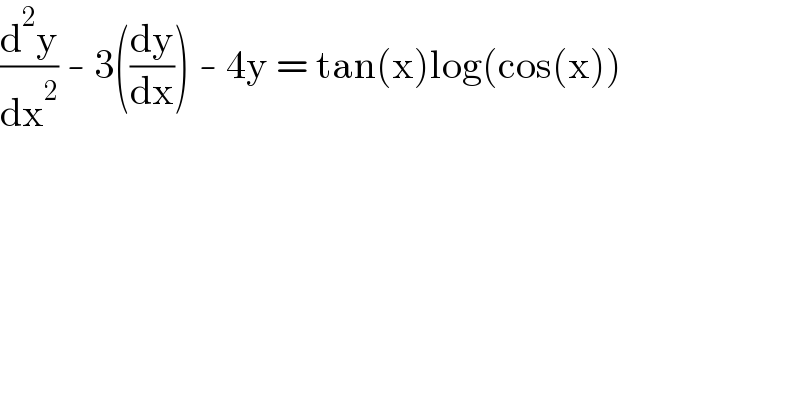
(d^2 y/dx^2 ) - 3((dy/dx)) - 4y = tan(x)log(cos(x))
$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:-\:\mathrm{3}\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)\:-\:\mathrm{4y}\:=\:\mathrm{tan}\left(\mathrm{x}\right)\mathrm{log}\left(\mathrm{cos}\left(\mathrm{x}\right)\right) \\ $$
Answered by Ar Brandon last updated on 29/Dec/21
y′′−3y′−4y=tanx∙ln(cosx) For y_(gh) : r^2 −3r−4=0⇒r=((3±5)/2) y_(gh) =ae^(4x) +be^(−x) By varying parameters, let y_p =a(x)e^(4x) +b(x)e^(−x) { ((a′(x)e^(4x) +b′(x)e^(−x) =0)),((4a′(x)e^(4x) −b′(x)e^(−x) =tanxln(cosx))) :} W= determinant ((e^(4x) ,e^(−x) ),((4e^(4x) ),(−e^(−x) )))=−e^(3x) −4e^(−3x) =−3e^(−3x) ≠0 W_a = determinant ((0,e^(−x) ),((tanxln(cosx)),(−e^(−x) )))=e^(−x) tanxln(cosx) W_b = determinant ((e^(4x) ,0),((4e^x ),(tanxln(cosx))))=e^(4x) tanxln(cosx) a(x)=∫(W_a /W)dx=−(1/3)∫e^(2x) tanxln(cosx)dx b(x)=∫(W_b /W)dx=−(1/3)∫e^(7x) tanxln(cosx)dx
$$\mathrm{y}''−\mathrm{3y}'−\mathrm{4y}=\mathrm{tan}{x}\centerdot\mathrm{ln}\left(\mathrm{cos}{x}\right) \\ $$$$\mathrm{For}\:\mathrm{y}_{\mathrm{gh}} :\:{r}^{\mathrm{2}} −\mathrm{3}{r}−\mathrm{4}=\mathrm{0}\Rightarrow{r}=\frac{\mathrm{3}\pm\mathrm{5}}{\mathrm{2}} \\ $$$$\mathrm{y}_{{gh}} ={ae}^{\mathrm{4}{x}} +{be}^{−{x}} \\ $$$$\mathrm{By}\:\mathrm{varying}\:\mathrm{parameters},\:\mathrm{let} \\ $$$$\mathrm{y}_{\mathrm{p}} ={a}\left({x}\right){e}^{\mathrm{4}{x}} +{b}\left({x}\right){e}^{−{x}} \\ $$$$\begin{cases}{{a}'\left({x}\right){e}^{\mathrm{4}{x}} +{b}'\left({x}\right){e}^{−{x}} =\mathrm{0}}\\{\mathrm{4}{a}'\left({x}\right){e}^{\mathrm{4}{x}} −{b}'\left({x}\right){e}^{−{x}} =\mathrm{tan}{x}\mathrm{ln}\left(\mathrm{cos}{x}\right)}\end{cases} \\ $$$$\mathrm{W}=\begin{vmatrix}{{e}^{\mathrm{4}{x}} }&{{e}^{−{x}} }\\{\mathrm{4}{e}^{\mathrm{4}{x}} }&{−{e}^{−{x}} }\end{vmatrix}=−{e}^{\mathrm{3}{x}} −\mathrm{4}{e}^{−\mathrm{3}{x}} =−\mathrm{3}{e}^{−\mathrm{3}{x}} \neq\mathrm{0} \\ $$$$\mathrm{W}_{{a}} =\begin{vmatrix}{\mathrm{0}}&{{e}^{−{x}} }\\{\mathrm{tan}{x}\mathrm{ln}\left(\mathrm{cos}{x}\right)}&{−{e}^{−{x}} }\end{vmatrix}={e}^{−{x}} \mathrm{tan}{x}\mathrm{ln}\left(\mathrm{cos}{x}\right) \\ $$$$\mathrm{W}_{{b}} =\begin{vmatrix}{{e}^{\mathrm{4}{x}} }&{\mathrm{0}}\\{\mathrm{4}{e}^{{x}} }&{\mathrm{tan}{x}\mathrm{ln}\left(\mathrm{cos}{x}\right)}\end{vmatrix}={e}^{\mathrm{4}{x}} \mathrm{tan}{x}\mathrm{ln}\left(\mathrm{cos}{x}\right) \\ $$$${a}\left({x}\right)=\int\frac{\mathrm{W}_{{a}} }{\mathrm{W}}{dx}=−\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{\mathrm{2}{x}} \mathrm{tan}{x}\mathrm{ln}\left(\mathrm{cos}{x}\right){dx} \\ $$$${b}\left({x}\right)=\int\frac{\mathrm{W}_{{b}} }{\mathrm{W}}{dx}=−\frac{\mathrm{1}}{\mathrm{3}}\int{e}^{\mathrm{7}{x}} \mathrm{tan}{x}\mathrm{ln}\left(\mathrm{cos}{x}\right){dx} \\ $$
Commented by HongKing last updated on 29/Dec/21
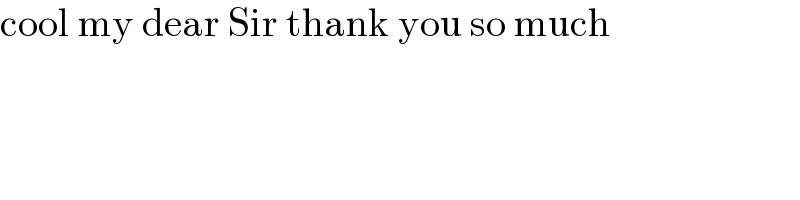
cool my dear Sir thank you so much
$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
Commented by HongKing last updated on 29/Dec/21
but what is the general solution dear Sir
$$\mathrm{but}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
Commented by Ar Brandon last updated on 29/Dec/21
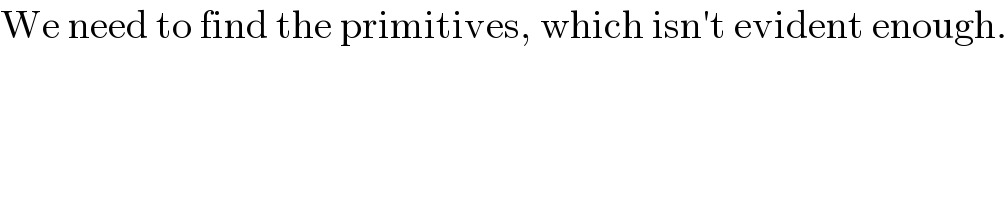
We need to find the primitives, which isn′t evident enough.
$$\mathrm{We}\:\mathrm{need}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{primitives},\:\mathrm{which}\:\mathrm{isn}'\mathrm{t}\:\mathrm{evident}\:\mathrm{enough}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *