Menu Close

d-2-y-dx-2-4-dy-dx-11y-e-2x-sin-4x-

Tinku Tara 0 Comments
Pin




Question Number 123107 by benjo_mathlover last updated on 23/Nov/20
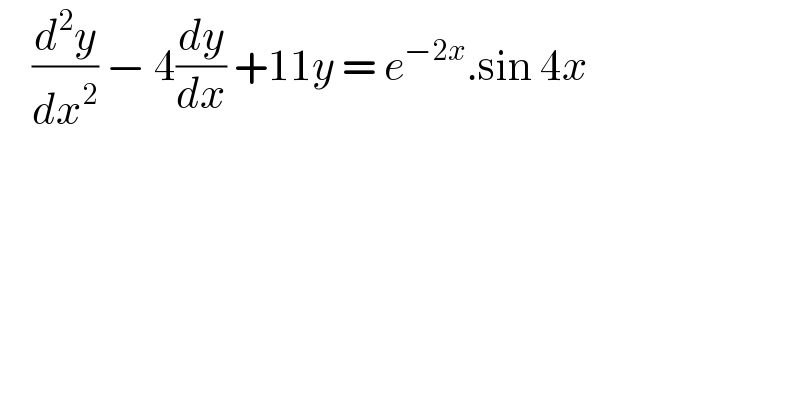
(d^2 y/dx^2 ) − 4(dy/dx) +11y = e^(−2x) .sin 4x
$$\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:−\:\mathrm{4}\frac{{dy}}{{dx}}\:+\mathrm{11}{y}\:=\:{e}^{−\mathrm{2}{x}} .\mathrm{sin}\:\mathrm{4}{x}\: \\ $$
Answered by mathmax by abdo last updated on 23/Nov/20
h→y^(′′) −4y^′ +11y =0→r^2 −4r+11=0 Δ^′ =4−11=−7 ⇒r_1 =2+i(√7) and r_2 =2−i(√7) y_h =ae^((2+i(√7))x) +b e^((2−i(√7))x) =e^(2x) (αcos((√7)x)+β sin((√7)x)) =αu_1 +βu_2 W(u_1 ,u_2 ) = determinant (((e^(2x) cos((√7)x) e^(2x) sin((√7)x))),((e^(2x) (2cos((√7)x)−(√7)sin((√7))x e^(2x) (2sin((√7)x)+(√7)cos((√7)x)))) =e^(4x) {2cos((√7)x)sin((√7)x)+(√7)cos^2 ((√7)x)} −e^(4x) {2sin((√7)x)cos((√7)x)−(√7)sin^2 ((√7)x)} =(√7)e^(4x) ≠0 W_1 = determinant (((0 e^(2x) sin((√7)x))),((e^(−2x) sin(4x) e^(2x) (2sin((√7)x)+(√7)cos((√7)x)))) =−sin(4x)sin((√7)x) W_2 = determinant (((e^(2x) cos((√7)x) 0)),((e^(2x) (2cos((√7)x)−(√7)sin((√7)x) e^(−2x) sin(4x)))) =cos((√7)x)sin(4x) v_1 =∫ (w_1 /w)dx =−∫ ((sin(4x)sin((√7)x))/( (√7)e^(4x) ))dx =(1/( (√7)))∫ e^(−4x) sin(4x)sin((√7)x)dx (eazy to find by use sina.sinb=....) v_2 =∫ (w_2 /w)dx =∫ ((cos((√7)x)sin(4x))/( (√7)e^(4x) ))dx =(1/( (√7)))∫ e^(−4x) cos((√7)x)sin(4x)dx =.....(use trigo.formulae) ⇒y_p =u_1 v_1 +u_2 v_2 the general solution is y =y_h +y_p
$$\mathrm{h}\rightarrow\mathrm{y}^{''} −\mathrm{4y}^{'} \:+\mathrm{11y}\:=\mathrm{0}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{4r}+\mathrm{11}=\mathrm{0} \\ $$$$\Delta^{'} \:=\mathrm{4}−\mathrm{11}=−\mathrm{7}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\mathrm{2}+\mathrm{i}\sqrt{\mathrm{7}}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\mathrm{2}−\mathrm{i}\sqrt{\mathrm{7}} \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{ae}^{\left(\mathrm{2}+\mathrm{i}\sqrt{\mathrm{7}}\right)\mathrm{x}} \:+\mathrm{b}\:\mathrm{e}^{\left(\mathrm{2}−\mathrm{i}\sqrt{\mathrm{7}}\right)\mathrm{x}} \:=\mathrm{e}^{\mathrm{2x}} \left(\alpha\mathrm{cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)+\beta\:\mathrm{sin}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\right)\:=\alpha\mathrm{u}_{\mathrm{1}} \:+\beta\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{2x}} \mathrm{cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\:\:\:\:\mathrm{e}^{\mathrm{2x}} \mathrm{sin}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)}\\{\mathrm{e}^{\mathrm{2x}} \left(\mathrm{2cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)−\sqrt{\mathrm{7}}\mathrm{sin}\left(\sqrt{\mathrm{7}}\right)\mathrm{x}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} \left(\mathrm{2sin}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)+\sqrt{\mathrm{7}}\mathrm{cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\right.\right.}\end{vmatrix} \\ $$$$=\mathrm{e}^{\mathrm{4x}} \left\{\mathrm{2cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\mathrm{sin}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)+\sqrt{\mathrm{7}}\mathrm{cos}^{\mathrm{2}} \left(\sqrt{\mathrm{7}}\mathrm{x}\right)\right\} \\ $$$$−\mathrm{e}^{\mathrm{4x}} \left\{\mathrm{2sin}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\mathrm{cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)−\sqrt{\mathrm{7}}\mathrm{sin}^{\mathrm{2}} \left(\sqrt{\mathrm{7}}\mathrm{x}\right)\right\} \\ $$$$=\sqrt{\mathrm{7}}\mathrm{e}^{\mathrm{4x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} \:\mathrm{sin}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)}\\{\mathrm{e}^{−\mathrm{2x}} \mathrm{sin}\left(\mathrm{4x}\right)\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} \left(\mathrm{2sin}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)+\sqrt{\mathrm{7}}\mathrm{cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\right.}\end{vmatrix} \\ $$$$=−\mathrm{sin}\left(\mathrm{4x}\right)\mathrm{sin}\left(\sqrt{\mathrm{7}}\mathrm{x}\right) \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{2x}} \mathrm{cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{e}^{\mathrm{2x}} \left(\mathrm{2cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)−\sqrt{\mathrm{7}}\mathrm{sin}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{sin}\left(\mathrm{4x}\right)\right.}\end{vmatrix} \\ $$$$=\mathrm{cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\mathrm{sin}\left(\mathrm{4x}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\int\:\frac{\mathrm{sin}\left(\mathrm{4x}\right)\mathrm{sin}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)}{\:\sqrt{\mathrm{7}}\mathrm{e}^{\mathrm{4x}} }\mathrm{dx}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{7}}}\int\:\mathrm{e}^{−\mathrm{4x}} \:\mathrm{sin}\left(\mathrm{4x}\right)\mathrm{sin}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\mathrm{dx} \\ $$$$\left(\mathrm{eazy}\:\mathrm{to}\:\mathrm{find}\:\mathrm{by}\:\mathrm{use}\:\mathrm{sina}.\mathrm{sinb}=….\right) \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\frac{\mathrm{cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\mathrm{sin}\left(\mathrm{4x}\right)}{\:\sqrt{\mathrm{7}}\mathrm{e}^{\mathrm{4x}} }\mathrm{dx}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{7}}}\int\:\:\mathrm{e}^{−\mathrm{4x}} \:\mathrm{cos}\left(\sqrt{\mathrm{7}}\mathrm{x}\right)\mathrm{sin}\left(\mathrm{4x}\right)\mathrm{dx} \\ $$$$=…..\left(\mathrm{use}\:\mathrm{trigo}.\mathrm{formulae}\right)\:\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} +\mathrm{y}_{\mathrm{p}} \\ $$
Commented by peter frank last updated on 24/Nov/20
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by talminator2856791 last updated on 08/Dec/20
how do you make big line like that
$$\:\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{make}\:\mathrm{big}\:\mathrm{line}\:\mathrm{like}\:\mathrm{that} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *