Menu Close

d-2-y-dx-2-4-dy-dx-y-a-sin-2x-

Tinku Tara 0 Comments
Pin




Question Number 105603 by bemath last updated on 30/Jul/20
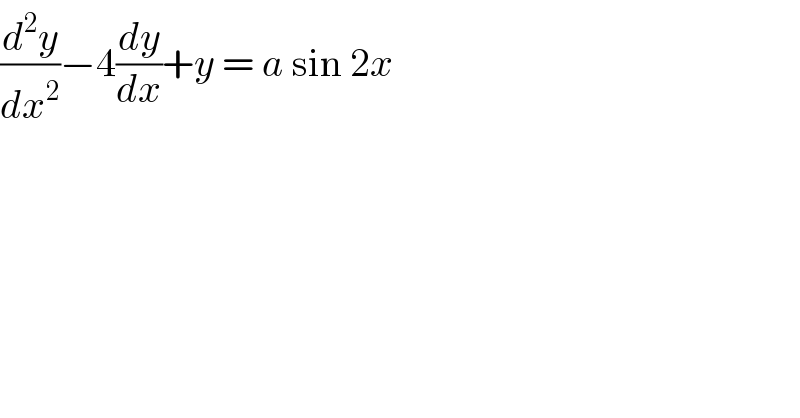
(d^2 y/dx^2 )−4(dy/dx)+y = a sin 2x
$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }−\mathrm{4}\frac{{dy}}{{dx}}+{y}\:=\:{a}\:\mathrm{sin}\:\mathrm{2}{x} \\ $$
Answered by bobhans last updated on 30/Jul/20
Homogenous equation ν^2 −4ν+1=0 →ν=((4±2(√3))/2) ν=2±(√3) ⇒y_h = C_1 e^((2+(√3))x) +C_2 e^((2−(√3))x) Let particular solution y_p = Asin 2x+Bcos 2x y_p ′=2Acos 2x−2Bsin 2x y_p ′′=−4Asin 2x−4Bcos 2x comparing coefficient LHS and RHS { ((8B−3A=a)),((8A=3B)) :} { ((A=((3a)/(55)) & B=((24a)/(165)))),((y_p = ((3a)/(55))sin 2x+ ((24a)/(165))cos 2x)) :} complete solution y = C_1 e^((2+(√3))x) +C_2 e^((2−(√3))x) +((3a)/(55))sin 2x+((24a)/(165))cos 2x ★
$$\mathcal{H}{omogenous}\:{equation} \\ $$$$\nu^{\mathrm{2}} −\mathrm{4}\nu+\mathrm{1}=\mathrm{0}\:\rightarrow\nu=\frac{\mathrm{4}\pm\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\nu=\mathrm{2}\pm\sqrt{\mathrm{3}}\:\Rightarrow{y}_{{h}} =\:{C}_{\mathrm{1}} {e}^{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){x}} +{C}_{\mathrm{2}} {e}^{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){x}} \\ $$$${Let}\:{particular}\:{solution}\: \\ $$$${y}_{{p}} =\:{A}\mathrm{sin}\:\mathrm{2}{x}+{B}\mathrm{cos}\:\mathrm{2}{x} \\ $$$${y}_{{p}} '=\mathrm{2}{A}\mathrm{cos}\:\mathrm{2}{x}−\mathrm{2}{B}\mathrm{sin}\:\mathrm{2}{x} \\ $$$${y}_{{p}} ''=−\mathrm{4}{A}\mathrm{sin}\:\mathrm{2}{x}−\mathrm{4}{B}\mathrm{cos}\:\mathrm{2}{x} \\ $$$${comparing}\:{coefficient}\:{LHS}\:{and}\:{RHS} \\ $$$$\begin{cases}{\mathrm{8}{B}−\mathrm{3}{A}={a}}\\{\mathrm{8}{A}=\mathrm{3}{B}}\end{cases} \\ $$$$\begin{cases}{{A}=\frac{\mathrm{3}{a}}{\mathrm{55}}\:\&\:{B}=\frac{\mathrm{24}{a}}{\mathrm{165}}}\\{{y}_{{p}} =\:\frac{\mathrm{3}{a}}{\mathrm{55}}\mathrm{sin}\:\mathrm{2}{x}+\:\frac{\mathrm{24}{a}}{\mathrm{165}}\mathrm{cos}\:\mathrm{2}{x}}\end{cases} \\ $$$${complete}\:{solution} \\ $$$${y}\:=\:{C}_{\mathrm{1}} {e}^{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right){x}} +{C}_{\mathrm{2}} {e}^{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){x}} +\frac{\mathrm{3}{a}}{\mathrm{55}}\mathrm{sin}\:\mathrm{2}{x}+\frac{\mathrm{24}{a}}{\mathrm{165}}\mathrm{cos}\:\mathrm{2}{x} \\ $$$$\bigstar \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 01/Aug/20
y^(′′) −4y^′ +y =asin(2x) h→r^2 −4r +1 =0 →Δ′ =4−1 =3 ⇒r_1 =2+(√3)and r_2 =2−(√3) ⇒y_h =α e^((2+(√3))x) +β e^((2−(√3))x) =αu_1 +β u_2 W(u_1 ,u_2 ) = determinant (((e^((2+(√3))x) e^((2−(√3))x) )),(((2+(√3)e^((2+(√3))x) (2−(√3))e^((2−(√3))x) ))) =(2−(√3))e^(4x) −(2+(√3))e^(4x) =−2(√3)e^(4x) ≠0 W_1 = determinant (((o e^((2−(√3))x) )),((asin(2x) (2−(√3))e^((2−(√3))x) )))=−a e^((2−(√3))x) sin(2x) W_2 = determinant (((e^((2+(√3))x) 0)),(((2+(√3))e^((2+(√3))x) asin(2x))))=a e^((2+(√3))x) sin(2x) v_1 =∫ (w_1 /w)dx =−∫ ((a e^((2−(√3))x) sin(2x))/(−2(√3)e^(4x) ))dx =(a/(2(√3)))∫ e^((−2−(√3))x) sin(2x)dx =(a/(2(√3))) Im(∫ e^(−(2+(√3))x+2ix) dx) but ∫ e^(−(2+(√3)+2i)x) dx =−(1/(2+(√3)+2i)) e^(−(2+(√3)+2i)x) =−((2+(√3)−2i)/((2+(√3))^2 +4)) e^(−(2+(√3))x) {cos(2x)+isin(2x)} =... v_2 =∫ (w_2 /w)dx =∫ ((a e^((2+(√3))x) sin(2x))/(−2(√3)e^(4x) ))dx =−(a/(2(√3)))∫ e^((−2+(√3))x) sin(2x)dx =−(a/(2(√3))) Im(∫ e^((−2+(√3)+2i)x) dx) and ∫ e^((−2+(√3)+2i)x) dx =(1/(−2+(√3)+2i)) e^((−2+(√3)+2i)x) =−(1/(2−(√3)−2i))e^((−2+(√3)+2i)x) =−((2−(√3)+2i)/((2−(√3))^2 +4))e^((−2+(√3))x) {cos(2x)+isin(2x)} rest to finish tbe calculus... ⇒y_p =u_1 v_1 +u_2 v_2 ⇒the general solution is y =y_h +y_p
$$\mathrm{y}^{''} −\mathrm{4y}^{'} \:+\mathrm{y}\:=\mathrm{asin}\left(\mathrm{2x}\right) \\ $$$$\mathrm{h}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{4r}\:+\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta'\:=\mathrm{4}−\mathrm{1}\:=\mathrm{3}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\mathrm{2}+\sqrt{\mathrm{3}}\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{h}} \:=\alpha\:\mathrm{e}^{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{x}} \:+\beta\:\mathrm{e}^{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{x}} \:=\alpha\mathrm{u}_{\mathrm{1}} \:+\beta\:\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{x}} }\\{\left(\mathrm{2}+\sqrt{\mathrm{3}}\mathrm{e}^{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{x}} \:\:\:\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{e}^{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{x}} \right.}\end{vmatrix} \\ $$$$=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{e}^{\mathrm{4x}} −\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{e}^{\mathrm{4x}} \:=−\mathrm{2}\sqrt{\mathrm{3}}\mathrm{e}^{\mathrm{4x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{x}} }\\{\mathrm{asin}\left(\mathrm{2x}\right)\:\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{e}^{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{x}} }\end{vmatrix}=−\mathrm{a}\:\mathrm{e}^{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{x}} \mathrm{sin}\left(\mathrm{2x}\right) \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{e}^{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{x}} \:\:\:\:\mathrm{asin}\left(\mathrm{2x}\right)}\end{vmatrix}=\mathrm{a}\:\mathrm{e}^{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{x}} \mathrm{sin}\left(\mathrm{2x}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\int\:\:\frac{\mathrm{a}\:\mathrm{e}^{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{x}} \mathrm{sin}\left(\mathrm{2x}\right)}{−\mathrm{2}\sqrt{\mathrm{3}}\mathrm{e}^{\mathrm{4x}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\int\:\:\mathrm{e}^{\left(−\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{x}} \mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx}\:=\frac{\mathrm{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\mathrm{Im}\left(\int\:\mathrm{e}^{−\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{x}+\mathrm{2ix}} \mathrm{dx}\right)\:\mathrm{but} \\ $$$$\int\:\:\mathrm{e}^{−\left(\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2i}\right)\mathrm{x}} \mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2i}}\:\mathrm{e}^{−\left(\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2i}\right)\mathrm{x}} \\ $$$$=−\frac{\mathrm{2}+\sqrt{\mathrm{3}}−\mathrm{2i}}{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{4}}\:\mathrm{e}^{−\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{x}} \left\{\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{isin}\left(\mathrm{2x}\right)\right\}\:=… \\ $$$$\mathrm{v}_{\mathrm{2}} \:=\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\frac{\mathrm{a}\:\mathrm{e}^{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{x}} \mathrm{sin}\left(\mathrm{2x}\right)}{−\mathrm{2}\sqrt{\mathrm{3}}\mathrm{e}^{\mathrm{4x}} }\mathrm{dx}\:=−\frac{\mathrm{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\int\:\mathrm{e}^{\left(−\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{x}} \mathrm{sin}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$=−\frac{\mathrm{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\:\mathrm{Im}\left(\int\:\:\mathrm{e}^{\left(−\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2i}\right)\mathrm{x}} \mathrm{dx}\right)\:\mathrm{and} \\ $$$$\int\:\mathrm{e}^{\left(−\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2i}\right)\mathrm{x}} \mathrm{dx}\:=\frac{\mathrm{1}}{−\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2i}}\:\mathrm{e}^{\left(−\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2i}\right)\mathrm{x}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{3}}−\mathrm{2i}}\mathrm{e}^{\left(−\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2i}\right)\mathrm{x}} \:=−\frac{\mathrm{2}−\sqrt{\mathrm{3}}+\mathrm{2i}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:+\mathrm{4}}\mathrm{e}^{\left(−\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{x}} \left\{\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{isin}\left(\mathrm{2x}\right)\right\} \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{finish}\:\mathrm{tbe}\:\mathrm{calculus}… \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \:\Rightarrow\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *