Question Number 55597 by ajfour last updated on 27/Feb/19
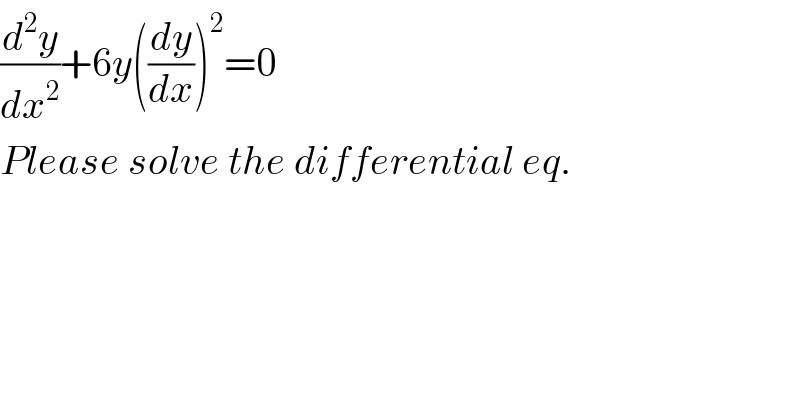
$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{6}{y}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${Please}\:{solve}\:{the}\:{differential}\:{eq}. \\ $$
Answered by mr W last updated on 27/Feb/19
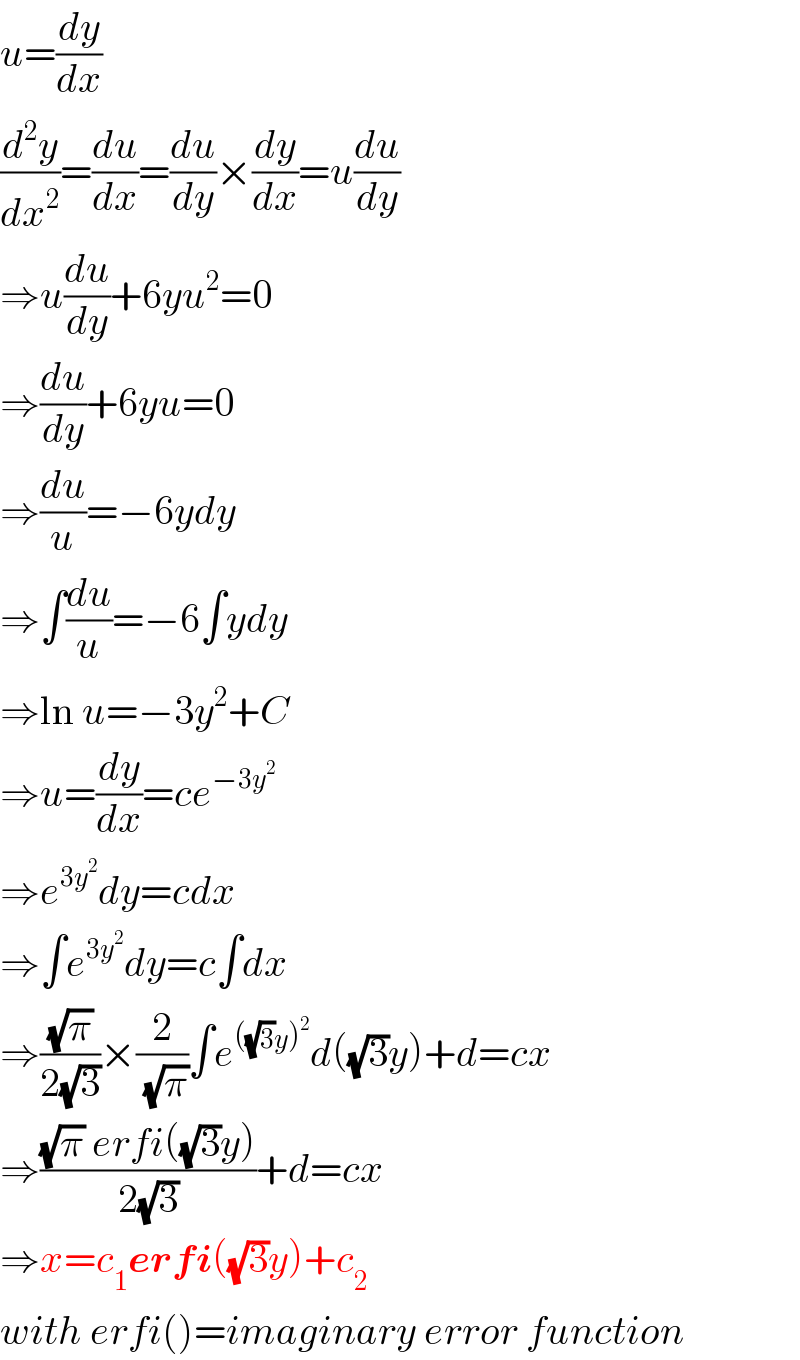
$${u}=\frac{{dy}}{{dx}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{du}}{{dx}}=\frac{{du}}{{dy}}×\frac{{dy}}{{dx}}={u}\frac{{du}}{{dy}} \\ $$$$\Rightarrow{u}\frac{{du}}{{dy}}+\mathrm{6}{yu}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{du}}{{dy}}+\mathrm{6}{yu}=\mathrm{0} \\ $$$$\Rightarrow\frac{{du}}{{u}}=−\mathrm{6}{ydy} \\ $$$$\Rightarrow\int\frac{{du}}{{u}}=−\mathrm{6}\int{ydy} \\ $$$$\Rightarrow\mathrm{ln}\:{u}=−\mathrm{3}{y}^{\mathrm{2}} +{C} \\ $$$$\Rightarrow{u}=\frac{{dy}}{{dx}}={ce}^{−\mathrm{3}{y}^{\mathrm{2}} } \\ $$$$\Rightarrow{e}^{\mathrm{3}{y}^{\mathrm{2}} } {dy}={cdx} \\ $$$$\Rightarrow\int{e}^{\mathrm{3}{y}^{\mathrm{2}} } {dy}={c}\int{dx} \\ $$$$\Rightarrow\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{3}}}×\frac{\mathrm{2}}{\:\sqrt{\pi}}\int{e}^{\left(\sqrt{\mathrm{3}}{y}\right)^{\mathrm{2}} } {d}\left(\sqrt{\mathrm{3}}{y}\right)+{d}={cx} \\ $$$$\Rightarrow\frac{\sqrt{\pi}\:{erfi}\left(\sqrt{\mathrm{3}}{y}\right)}{\mathrm{2}\sqrt{\mathrm{3}}}+{d}={cx} \\ $$$$\Rightarrow{x}={c}_{\mathrm{1}} \boldsymbol{{erfi}}\left(\sqrt{\mathrm{3}}{y}\right)+{c}_{\mathrm{2}} \\ $$$${with}\:{erfi}\left(\right)={imaginary}\:{error}\:{function} \\ $$
Commented by mr W last updated on 27/Feb/19

Commented by mr W last updated on 27/Feb/19
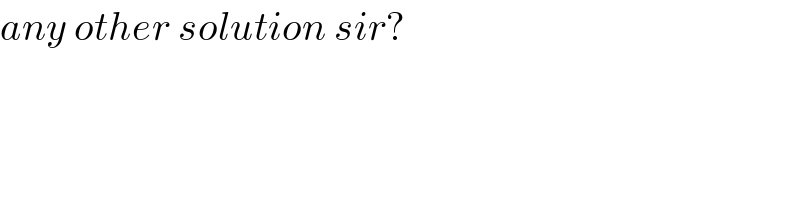
$${any}\:{other}\:{solution}\:{sir}? \\ $$
Commented by ajfour last updated on 27/Feb/19
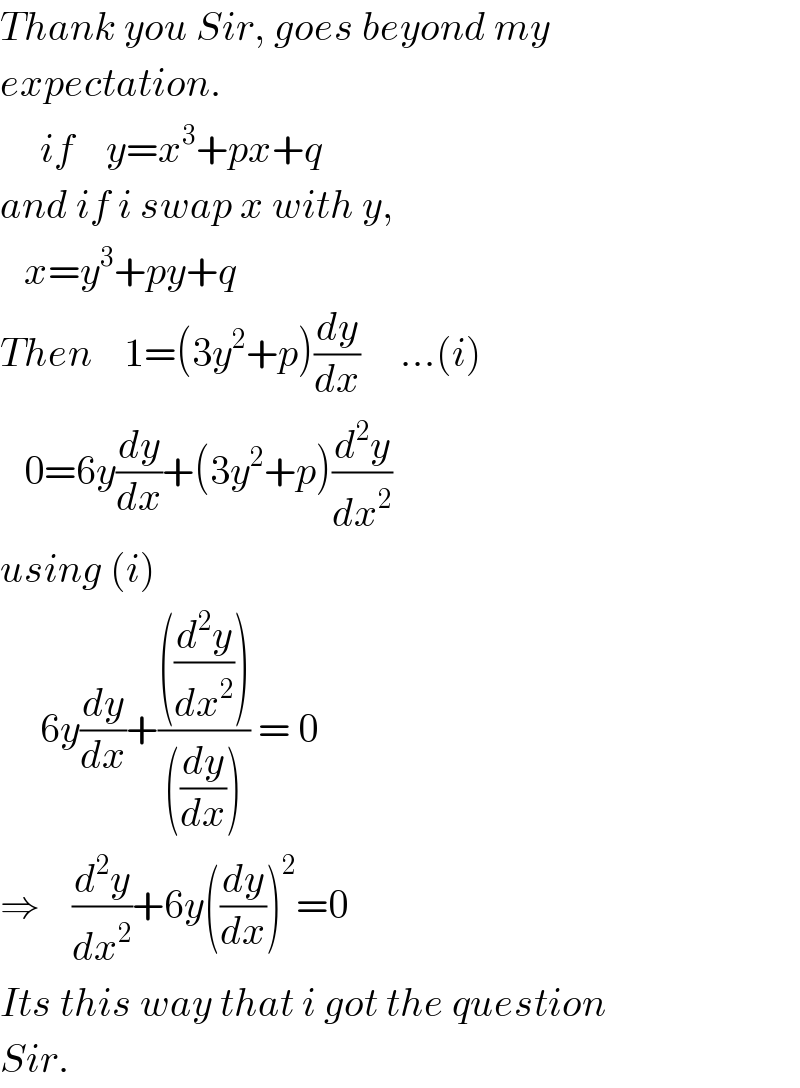
$${Thank}\:{you}\:{Sir},\:{goes}\:{beyond}\:{my} \\ $$$${expectation}. \\ $$$$\:\:\:\:\:{if}\:\:\:\:{y}={x}^{\mathrm{3}} +{px}+{q} \\ $$$${and}\:{if}\:{i}\:{swap}\:{x}\:{with}\:{y}, \\ $$$$\:\:\:{x}={y}^{\mathrm{3}} +{py}+{q} \\ $$$${Then}\:\:\:\:\mathrm{1}=\left(\mathrm{3}{y}^{\mathrm{2}} +{p}\right)\frac{{dy}}{{dx}}\:\:\:\:\:…\left({i}\right) \\ $$$$\:\:\:\mathrm{0}=\mathrm{6}{y}\frac{{dy}}{{dx}}+\left(\mathrm{3}{y}^{\mathrm{2}} +{p}\right)\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} } \\ $$$${using}\:\left({i}\right) \\ $$$$\:\:\:\:\:\mathrm{6}{y}\frac{{dy}}{{dx}}+\frac{\left(\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right)}{\left(\frac{{dy}}{{dx}}\right)}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{6}{y}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${Its}\:{this}\:{way}\:{that}\:{i}\:{got}\:{the}\:{question} \\ $$$${Sir}. \\ $$
Commented by ajfour last updated on 27/Feb/19
![knowing then that other solution is y^3 +py+q = x only we need to write y in terms of x. let y=u+v (u+v)^3 +p(u+v)+q=x u^3 +v^3 +(u+v)[3uv+p]=x−q let uv=−(p/3) ⇒ (uv)^3 =−(p^3 /(27)) ⇒ u^3 +v^3 =x−q ⇒ u^3 , v^3 are roots of z^2 −(x−q)z−(p^3 /(27)) =0 u^3 , v^3 = ((x−q)/2)±(√((((x−q)/2))^2 +(p^3 /(27)))) hence our y(x) can even be y=[((x−q)/2)+(√((((x−q)/2))^2 +(p^3 /(27)))) ]^(1/3) +[((x−q)/2)−(√((((x−q)/2))^2 +(p^3 /(27)))) ]^(1/3) p, q being the arbitrary constants. (∵_⌣ ) Congratulations Sir, its you who found the new cubic formula.](https://www.tinkutara.com/question/Q55611.png)
$${knowing}\:{then}\:{that}\:{other}\:{solution} \\ $$$${is}\:\:\:\:\:\:{y}^{\mathrm{3}} +{py}+{q}\:=\:{x} \\ $$$${only}\:{we}\:{need}\:{to}\:{write}\:{y}\:{in}\:{terms} \\ $$$${of}\:{x}. \\ $$$$\:\:\:\:\:\:\:\:\:\:{let}\:\:\:{y}={u}+{v} \\ $$$$\:\:\:\left({u}+{v}\right)^{\mathrm{3}} +{p}\left({u}+{v}\right)+{q}={x} \\ $$$$\:\:\:{u}^{\mathrm{3}} +{v}^{\mathrm{3}} +\left({u}+{v}\right)\left[\mathrm{3}{uv}+{p}\right]={x}−{q} \\ $$$$\:\:\:\:{let}\:\:\:{uv}=−\frac{{p}}{\mathrm{3}}\:\:\:\Rightarrow\:\:\left({uv}\right)^{\mathrm{3}} =−\frac{{p}^{\mathrm{3}} }{\mathrm{27}} \\ $$$$\Rightarrow\:\:\:\:{u}^{\mathrm{3}} +{v}^{\mathrm{3}} \:={x}−{q} \\ $$$$\Rightarrow\:\:{u}^{\mathrm{3}} ,\:{v}^{\mathrm{3}} \:\:{are}\:{roots}\:{of} \\ $$$$\:\:\:\:\:\:{z}^{\mathrm{2}} −\left({x}−{q}\right){z}−\frac{{p}^{\mathrm{3}} }{\mathrm{27}}\:=\mathrm{0} \\ $$$$\:\:{u}^{\mathrm{3}} ,\:{v}^{\mathrm{3}} \:=\:\frac{{x}−{q}}{\mathrm{2}}\pm\sqrt{\left(\frac{{x}−{q}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{{p}^{\mathrm{3}} }{\mathrm{27}}} \\ $$$$\:\:\:{hence}\:{our}\:{y}\left({x}\right)\:{can}\:{even}\:{be} \\ $$$$\:\:\:\:{y}=\left[\frac{{x}−{q}}{\mathrm{2}}+\sqrt{\left(\frac{{x}−{q}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}\:\right]^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\left[\frac{{x}−{q}}{\mathrm{2}}−\sqrt{\left(\frac{{x}−{q}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}\:\right]^{\mathrm{1}/\mathrm{3}} \\ $$$${p},\:{q}\:{being}\:{the}\:{arbitrary}\:{constants}. \\ $$$$\:\:\:\:\:\:\:\left(\underset{\smallsmile} {\because}\right)\:\:{Congratulations}\:{Sir}, \\ $$$${its}\:{you}\:{who}\:{found}\:{the}\:{new}\:{cubic} \\ $$$${formula}. \\ $$
Commented by mr W last updated on 27/Feb/19
$${i}\:{need}\:{some}\:{time}\:{to}\:{catch}\:{you}\:{fully}. \\ $$
