Question Number 105659 by bemath last updated on 30/Jul/20
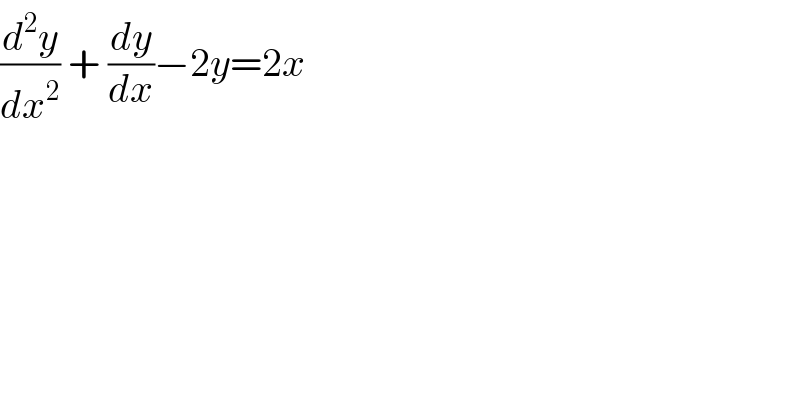
$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\frac{{dy}}{{dx}}−\mathrm{2}{y}=\mathrm{2}{x}\: \\ $$
Answered by john santu last updated on 30/Jul/20
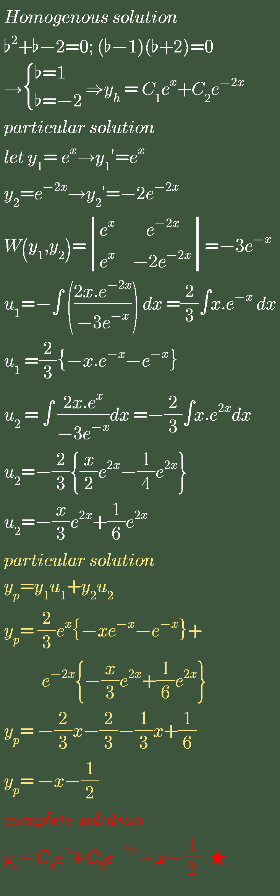
Commented by bramlex last updated on 31/Jul/20
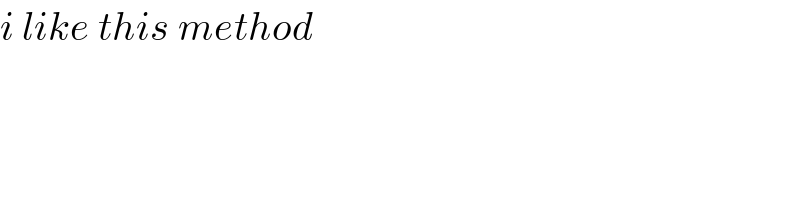
$${i}\:{like}\:{this}\:{method} \\ $$
Answered by mathmax by abdo last updated on 31/Jul/20
![laplace method y^(′′) +y^′ −2y =2x ⇒L(y^(′′) )+L(y^′ )−2L(y) =2L(x) ⇒x^2 L(y)−x y(o)−y^′ (o)+xL(y)−y(o)−2L(y) =2L(x) ⇒ (x^2 +x−2)L(y) =(x+1)y(0)+y^′ (o)+2L(x) but L(x) =∫_0 ^∞ t e^(−xt) dt =[(t/(−x))e^(−xt) ]_(t=0) ^∞ −∫_0 ^∞ (1/(−x))e^(−xt) dt =−(1/x)(o) +(1/x)[−(1/x)e^(−xt) ]_(t=0) ^∞ =(1/x^2 ) so e ⇒(x^2 +x−2)L(y) =(x+1)y(o)+y^′ (o)+(2/x^2 ) ⇒ L(y) =((x+1)/((x^2 +x−2)))y(o) +((y^′ (o))/(x^2 +x−2)) +(2/(x^2 (x^2 +x−2))) ⇒ y(x) =y_0 L^(−1) (((x+1)/(x^2 +x−2)))+y^′ (o)L^(−1) ((1/(x^2 +x−2)))+2L^(−1) ((1/(x^2 (x^2 +x−2)))) let f(x) =(1/(x^2 +x−2)) Δ =1+8 =9 ⇒x_1 =((−1+3)/2) =1 and x_2 =((−1−3)/2)=−2 ⇒ f(x) =(1/((x−1)(x+2))) =(1/3)((1/(x−1))−(1/(x+2))) ⇒ L^(−1) (f) =(1/3)e^x −(1/3)e^(−2x) g(x) =((x+1)/(x^2 +x+2)) =(a/(x−1)) +(b/(x+2))(=((x+1)/((x−1)(x+2)))) a =(2/3) and b =(1/3) ⇒g(x) =(2/(3(x−1))) +(1/(3(x+2))) ⇒ L^(−1) (g) =(2/3)e^x +(1/3)e^(−2x) h(x) =(1/(x^2 (x^2 +x−2))) =(a/x) +(b/x^2 ) +(c/(x−1)) +(d/(x+2))(eazy to find a_i ) ⇒ L^(−1) (h) =ae^x +bx +c e^x +d e^(−2x) ⇒ y(x) =y_0 ((2/3)e^x +(1/3)e^(−2x) ) +y^′ (0)((1/3)e^x −(1/3) e^(−2x) ) +2(ae^x +bx +ce^x +de^(−2x) ) at form y(x) =c_1 e^x +c_2 e^(−2x) +2bx +](https://www.tinkutara.com/question/Q105681.png)
$$\mathrm{laplace}\:\mathrm{method}\:\mathrm{y}^{''} \:+\mathrm{y}^{'} −\mathrm{2y}\:=\mathrm{2x}\:\Rightarrow\mathrm{L}\left(\mathrm{y}^{''} \right)+\mathrm{L}\left(\mathrm{y}^{'} \right)−\mathrm{2L}\left(\mathrm{y}\right)\:=\mathrm{2L}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} \mathrm{L}\left(\mathrm{y}\right)−\mathrm{x}\:\mathrm{y}\left(\mathrm{o}\right)−\mathrm{y}^{'} \left(\mathrm{o}\right)+\mathrm{xL}\left(\mathrm{y}\right)−\mathrm{y}\left(\mathrm{o}\right)−\mathrm{2L}\left(\mathrm{y}\right)\:=\mathrm{2L}\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{2}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\left(\mathrm{x}+\mathrm{1}\right)\mathrm{y}\left(\mathrm{0}\right)+\mathrm{y}^{'} \left(\mathrm{o}\right)+\mathrm{2L}\left(\mathrm{x}\right)\:\mathrm{but} \\ $$$$\mathrm{L}\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}\:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:=\left[\frac{\mathrm{t}}{−\mathrm{x}}\mathrm{e}^{−\mathrm{xt}} \right]_{\mathrm{t}=\mathrm{0}} ^{\infty} \:−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{−\mathrm{x}}\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{x}}\left(\mathrm{o}\right)\:+\frac{\mathrm{1}}{\mathrm{x}}\left[−\frac{\mathrm{1}}{\mathrm{x}}\mathrm{e}^{−\mathrm{xt}} \right]_{\mathrm{t}=\mathrm{0}} ^{\infty} \:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\:\mathrm{so} \\ $$$$\mathrm{e}\:\Rightarrow\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\left(\mathrm{x}+\mathrm{1}\right)\mathrm{y}\left(\mathrm{o}\right)+\mathrm{y}^{'} \left(\mathrm{o}\right)+\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{x}+\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}\right)}\mathrm{y}\left(\mathrm{o}\right)\:+\frac{\mathrm{y}^{'} \left(\mathrm{o}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}}\:+\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{2}\right)}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{y}_{\mathrm{0}} \mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}+\mathrm{1}}{{x}^{\mathrm{2}} \:+{x}−\mathrm{2}}\right)+{y}^{'} \left(\mathrm{o}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}}\right)+\mathrm{2L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}\right)}\right) \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}−\mathrm{2}} \\ $$$$\Delta\:=\mathrm{1}+\mathrm{8}\:=\mathrm{9}\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{3}}{\mathrm{2}}\:=\mathrm{1}\:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{3}}{\mathrm{2}}=−\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)}\:=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}\right)\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{f}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\mathrm{x}} −\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{2}}\:=\frac{\mathrm{a}}{\mathrm{x}−\mathrm{1}}\:+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{2}}\left(=\frac{\mathrm{x}+\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)}\right) \\ $$$$\mathrm{a}\:=\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{and}\:\mathrm{b}\:=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\mathrm{g}\left(\mathrm{x}\right)\:=\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{x}−\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{x}+\mathrm{2}\right)}\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{g}\right)\:=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{e}^{\mathrm{x}} \:+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{h}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{2}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}}\:+\frac{\mathrm{b}}{\mathrm{x}^{\mathrm{2}} }\:+\frac{\mathrm{c}}{\mathrm{x}−\mathrm{1}}\:+\frac{\mathrm{d}}{\mathrm{x}+\mathrm{2}}\left(\mathrm{eazy}\:\mathrm{to}\:\mathrm{find}\:\mathrm{a}_{\mathrm{i}} \right)\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{h}\right)\:=\mathrm{ae}^{\mathrm{x}} \:+\mathrm{bx}\:+\mathrm{c}\:\mathrm{e}^{\mathrm{x}} \:+\mathrm{d}\:\mathrm{e}^{−\mathrm{2x}} \:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{y}_{\mathrm{0}} \left(\frac{\mathrm{2}}{\mathrm{3}}\mathrm{e}^{\mathrm{x}} \:+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{−\mathrm{2x}} \right)\:+\mathrm{y}^{'} \left(\mathrm{0}\right)\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\mathrm{x}} −\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{e}^{−\mathrm{2x}} \right) \\ $$$$+\mathrm{2}\left(\mathrm{ae}^{\mathrm{x}} \:+\mathrm{bx}\:+\mathrm{ce}^{\mathrm{x}} \:+\mathrm{de}^{−\mathrm{2x}} \right)\:\:\mathrm{at}\:\mathrm{form} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{c}_{\mathrm{1}} \mathrm{e}^{\mathrm{x}} \:+\mathrm{c}_{\mathrm{2}} \mathrm{e}^{−\mathrm{2x}} \:+\mathrm{2bx}\:+ \\ $$
