Question Number 15706 by Joel577 last updated on 13/Jun/17
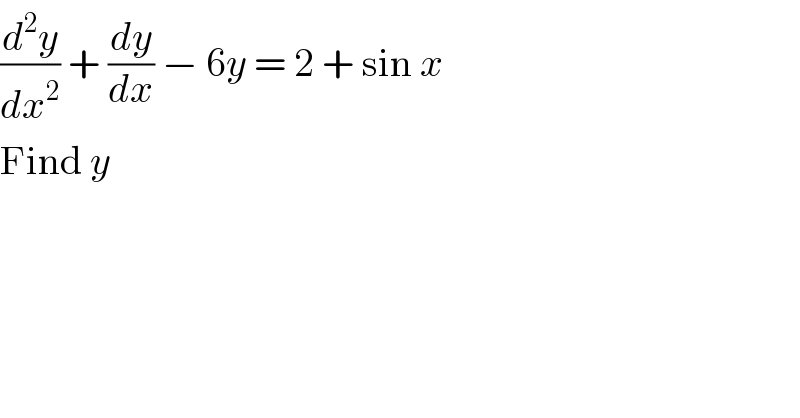
$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\frac{{dy}}{{dx}}\:−\:\mathrm{6}{y}\:=\:\mathrm{2}\:+\:\mathrm{sin}\:{x} \\ $$$$\mathrm{Find}\:{y} \\ $$
Commented by prakash jain last updated on 13/Jun/17

$$\mathrm{Characteristic}\:\mathrm{equation} \\ $$$$\lambda^{\mathrm{2}} +\lambda−\mathrm{6}=\mathrm{0} \\ $$$$\left(\lambda+\mathrm{3}\right)\left(\lambda−\mathrm{2}\right)=\mathrm{0} \\ $$$$\lambda=−\mathrm{3},\mathrm{2} \\ $$$${y}_{{h}} ={c}_{\mathrm{1}} {e}^{−\mathrm{3}{x}} +{c}_{\mathrm{2}} {e}^{\mathrm{2}{x}} \\ $$$$\mathrm{particular}\:\mathrm{solution} \\ $$$${y}={a}\mathrm{cos}\:{x}+{b}\mathrm{sin}\:{x}+{c} \\ $$$${y}'=−{a}\mathrm{sin}\:{x}+{b}\mathrm{cos}\:{x} \\ $$$${y}'^{'} =−{a}\mathrm{cos}\:{x}−{b}\mathrm{sin}\:{x} \\ $$$$−{a}\mathrm{cos}\:{x}−{b}\mathrm{sin}\:{x}−{a}\mathrm{sin}\:{x}+{b}\mathrm{cos}\:{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\mathrm{6}{a}\mathrm{cos}\:{x}−\mathrm{6}{b}\mathrm{sin}\:{x}−\mathrm{6}{c}=\mathrm{2}+\mathrm{sin}\:{x} \\ $$$${c}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$−\mathrm{7}{a}+{b}=\mathrm{0}\:\:\:\left({coefficient}\:{of}\:{cosx}\right) \\ $$$$−\mathrm{7}{b}−{a}=\mathrm{1}\Rightarrow−\mathrm{49}{b}−\mathrm{7}{a}=\mathrm{7}\Rightarrow{b}=−\frac{\mathrm{7}}{\mathrm{50}} \\ $$$${a}=−\frac{\mathrm{1}}{\mathrm{50}} \\ $$$${particular}\:{solution} \\ $$$${y}_{{p}} =−\frac{\mathrm{1}}{\mathrm{50}}\mathrm{cos}\:{x}−\frac{\mathrm{7}}{\mathrm{50}}\mathrm{sin}\:{x}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${y}={y}_{{h}} +{y}_{{p}} \\ $$$$={c}_{\mathrm{1}} {e}^{−\mathrm{3}{x}} +{c}_{\mathrm{2}} {e}^{\mathrm{2}{x}} −\frac{\mathrm{1}}{\mathrm{50}}\mathrm{cos}\:{x}−\frac{\mathrm{7}}{\mathrm{50}}\mathrm{sin}\:{x}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by Joel577 last updated on 13/Jun/17
$${thank}\:{you}\:{very}\:{much} \\ $$
