Question Number 121227 by benjo_mathlover last updated on 06/Nov/20

$$\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:\mathrm{e}^{−\mathrm{2x}} \: \\ $$
Answered by Lordose last updated on 06/Nov/20
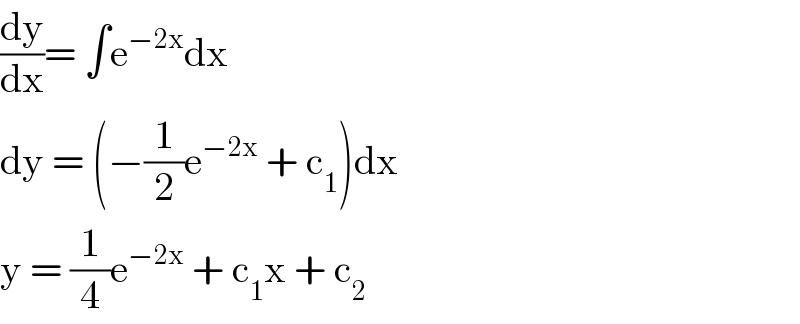
$$\frac{\mathrm{dy}}{\mathrm{dx}}=\:\int\mathrm{e}^{−\mathrm{2x}} \mathrm{dx} \\ $$$$\mathrm{dy}\:=\:\left(−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{2x}} \:+\:\mathrm{c}_{\mathrm{1}} \right)\mathrm{dx} \\ $$$$\mathrm{y}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\mathrm{2x}} \:+\:\mathrm{c}_{\mathrm{1}} \mathrm{x}\:+\:\mathrm{c}_{\mathrm{2}} \\ $$
