Question Number 115298 by Dwaipayan Shikari last updated on 24/Sep/20
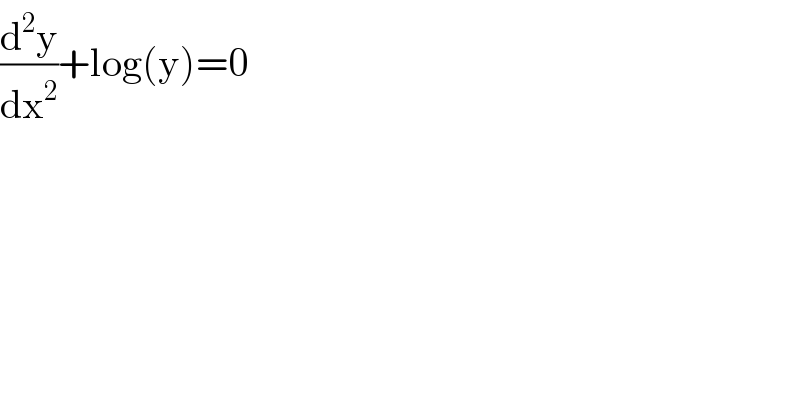
$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }+\mathrm{log}\left(\mathrm{y}\right)=\mathrm{0} \\ $$
Commented by mohammad17 last updated on 25/Sep/20
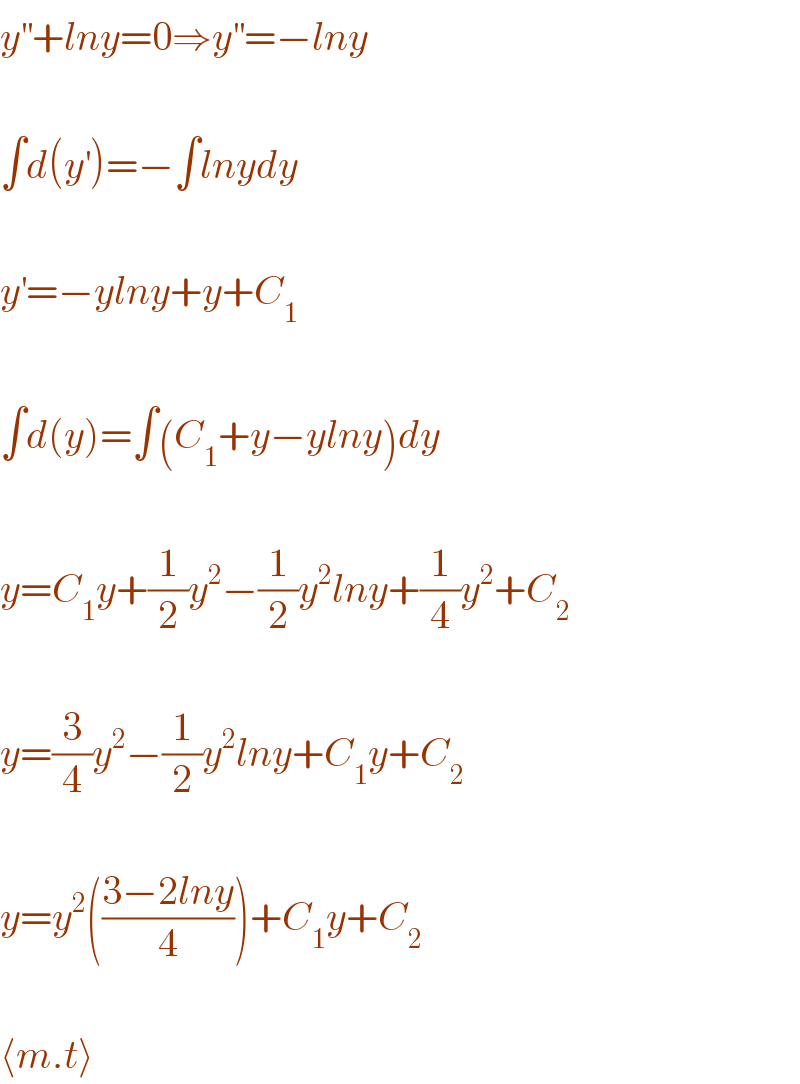
$${y}^{''} +{lny}=\mathrm{0}\Rightarrow{y}^{''} =−{lny} \\ $$$$ \\ $$$$\int{d}\left({y}^{'} \right)=−\int{lnydy} \\ $$$$ \\ $$$${y}^{'} =−{ylny}+{y}+{C}_{\mathrm{1}} \\ $$$$ \\ $$$$\int{d}\left({y}\right)=\int\left({C}_{\mathrm{1}} +{y}−{ylny}\right){dy} \\ $$$$ \\ $$$${y}={C}_{\mathrm{1}} {y}+\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} {lny}+\frac{\mathrm{1}}{\mathrm{4}}{y}^{\mathrm{2}} +{C}_{\mathrm{2}} \\ $$$$ \\ $$$${y}=\frac{\mathrm{3}}{\mathrm{4}}{y}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} {lny}+{C}_{\mathrm{1}} {y}+{C}_{\mathrm{2}} \\ $$$$ \\ $$$${y}={y}^{\mathrm{2}} \left(\frac{\mathrm{3}−\mathrm{2}{lny}}{\mathrm{4}}\right)+{C}_{\mathrm{1}} {y}+{C}_{\mathrm{2}} \\ $$$$ \\ $$$$\langle{m}.{t}\rangle \\ $$
Commented by Olaf last updated on 26/Sep/20

$${sorry}\:{mister}. \\ $$$$\int{d}\left({y}'\right)\:=\:−\int{lnydx}\:….! \\ $$$${and}\:{not}\:−\int{lnydy} \\ $$$${And}\:{as}\:{you}\:{can}\:{see}, \\ $$$${if}\:{you}\:{derivate}\:{your}\:{final}\:{result} \\ $$$${to}\:{verify}\:{the}\:{initial}\:{equation} \\ $$$${unafornately}\:{it}'{s}\:{wrong}. \\ $$
Answered by Olaf last updated on 24/Sep/20
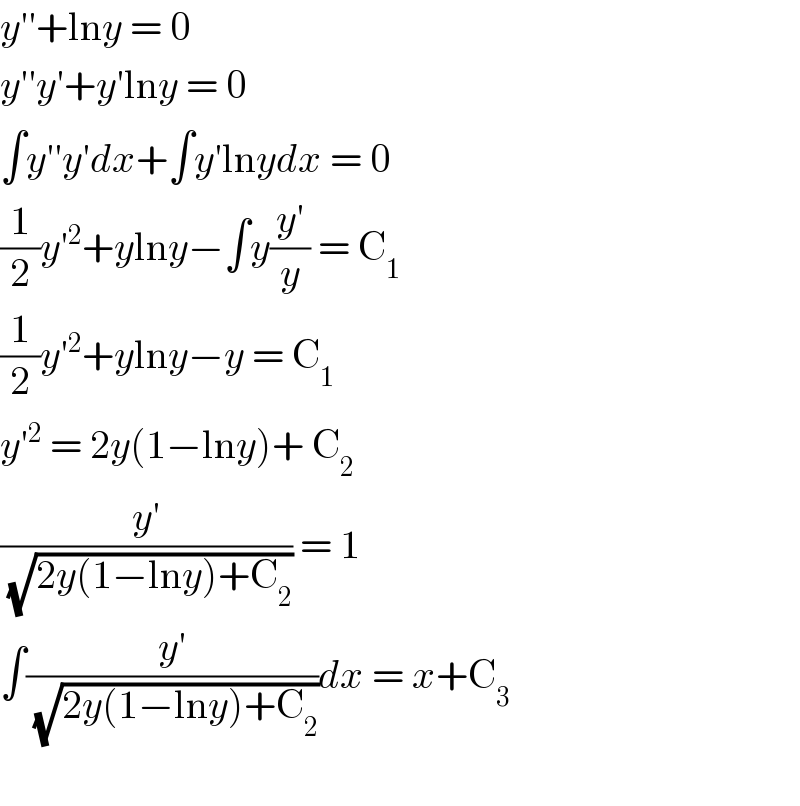
$${y}''+\mathrm{ln}{y}\:=\:\mathrm{0} \\ $$$${y}''{y}'+{y}'\mathrm{ln}{y}\:=\:\mathrm{0} \\ $$$$\int{y}''{y}'{dx}+\int{y}'\mathrm{ln}{ydx}\:=\:\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{y}'^{\mathrm{2}} +{y}\mathrm{ln}{y}−\int{y}\frac{{y}'}{{y}}\:=\:\mathrm{C}_{\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{y}'^{\mathrm{2}} +{y}\mathrm{ln}{y}−{y}\:=\:\mathrm{C}_{\mathrm{1}} \\ $$$${y}'^{\mathrm{2}} \:=\:\mathrm{2}{y}\left(\mathrm{1}−\mathrm{ln}{y}\right)+\:\mathrm{C}_{\mathrm{2}} \\ $$$$\frac{{y}'}{\:\sqrt{\mathrm{2}{y}\left(\mathrm{1}−\mathrm{ln}{y}\right)+\mathrm{C}_{\mathrm{2}} }}\:=\:\mathrm{1} \\ $$$$\int\frac{{y}'}{\:\sqrt{\mathrm{2}{y}\left(\mathrm{1}−\mathrm{ln}{y}\right)+\mathrm{C}_{\mathrm{2}} }}{dx}\:=\:{x}+\mathrm{C}_{\mathrm{3}} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 25/Sep/20
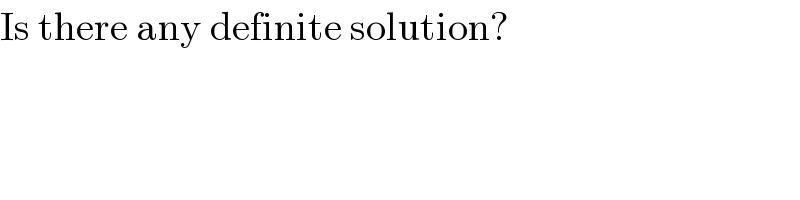
$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{definite}\:\mathrm{solution}? \\ $$
Commented by Olaf last updated on 26/Sep/20

$${no}\:{sir}. \\ $$$${only}\:{approximate}\:{solutions} \\ $$
