Question Number 126620 by fajri last updated on 22/Dec/20
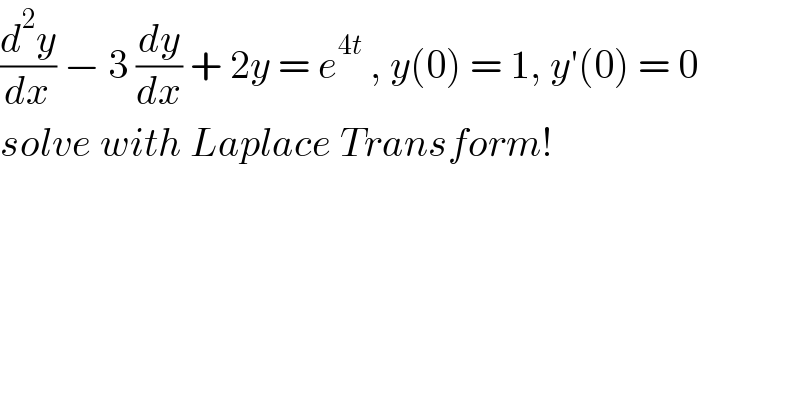
$$\frac{{d}^{\mathrm{2}} {y}}{{dx}}\:−\:\mathrm{3}\:\frac{{dy}}{{dx}}\:+\:\mathrm{2}{y}\:=\:{e}^{\mathrm{4}{t}} \:,\:{y}\left(\mathrm{0}\right)\:=\:\mathrm{1},\:{y}'\left(\mathrm{0}\right)\:=\:\mathrm{0} \\ $$$${solve}\:{with}\:{Laplace}\:{Transform}! \\ $$
Answered by Olaf last updated on 22/Dec/20
![(d^2 y/dx^2 )−3(dy/dx)+2y = e^(4t) [p^2 L(y)−py(0^− )−y′(0^− )]−3[pL(y)−y(0^− )] +2L(y) = (1/(p−4)) (p^2 −3p+2)L(y)−p+3 = (1/(p−4)) (p−1)(p−2)L(y) = (1/(p−4))+p−3 L(y) = ((1+(p−3)(p−4))/((p−1)(p−2)(p−4))) L(y) = ((7/3)/(p−1))−((3/2)/(p−2))+((1/6)/(p−4)) L^(−1) oL(y) = y = (7/3)e^t −(3/2)e^(2t) +(1/6)e^(4t)](https://www.tinkutara.com/question/Q126623.png)
$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }−\mathrm{3}\frac{{dy}}{{dx}}+\mathrm{2}{y}\:=\:{e}^{\mathrm{4}{t}} \\ $$$$\left[{p}^{\mathrm{2}} \mathfrak{L}\left({y}\right)−{py}\left(\mathrm{0}^{−} \right)−{y}'\left(\mathrm{0}^{−} \right)\right]−\mathrm{3}\left[{p}\mathfrak{L}\left({y}\right)−{y}\left(\mathrm{0}^{−} \right)\right] \\ $$$$+\mathrm{2}\mathfrak{L}\left({y}\right)\:=\:\frac{\mathrm{1}}{{p}−\mathrm{4}} \\ $$$$\left({p}^{\mathrm{2}} −\mathrm{3}{p}+\mathrm{2}\right)\mathfrak{L}\left({y}\right)−{p}+\mathrm{3}\:=\:\frac{\mathrm{1}}{{p}−\mathrm{4}} \\ $$$$\left({p}−\mathrm{1}\right)\left({p}−\mathrm{2}\right)\mathfrak{L}\left({y}\right)\:=\:\frac{\mathrm{1}}{{p}−\mathrm{4}}+{p}−\mathrm{3} \\ $$$$\mathfrak{L}\left({y}\right)\:=\:\frac{\mathrm{1}+\left({p}−\mathrm{3}\right)\left({p}−\mathrm{4}\right)}{\left({p}−\mathrm{1}\right)\left({p}−\mathrm{2}\right)\left({p}−\mathrm{4}\right)} \\ $$$$\mathfrak{L}\left({y}\right)\:=\:\frac{\mathrm{7}/\mathrm{3}}{{p}−\mathrm{1}}−\frac{\mathrm{3}/\mathrm{2}}{{p}−\mathrm{2}}+\frac{\mathrm{1}/\mathrm{6}}{{p}−\mathrm{4}} \\ $$$$\mathfrak{L}^{−\mathrm{1}} \mathrm{o}\mathfrak{L}\left({y}\right)\:=\:{y}\:=\:\frac{\mathrm{7}}{\mathrm{3}}{e}^{{t}} −\frac{\mathrm{3}}{\mathrm{2}}{e}^{\mathrm{2}{t}} +\frac{\mathrm{1}}{\mathrm{6}}{e}^{\mathrm{4}{t}} \\ $$
Commented by fajri last updated on 22/Dec/20
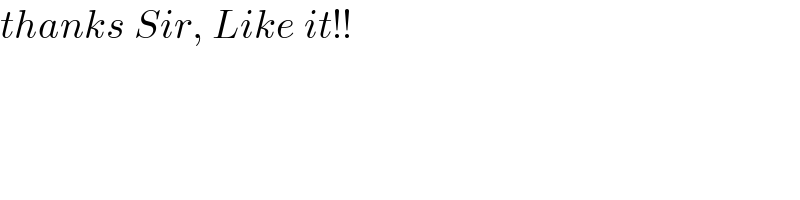
$${thanks}\:{Sir},\:{Like}\:{it}!! \\ $$
Answered by mathmax by abdo last updated on 22/Dec/20

$$\mathrm{wronskien}\:\mathrm{method}\:\:\:\:\mathrm{y}^{''} −\mathrm{3y}^{'} \:+\mathrm{2y}=\mathrm{e}^{\mathrm{4x}} \:\:\:\mathrm{with}\:\mathrm{y}\left(\mathrm{o}\right)=\mathrm{1}\:\mathrm{and}\:\mathrm{y}^{'} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\left.\mathrm{h}\right)\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{3r}\:+\mathrm{2}=\mathrm{0}\rightarrow\Delta=\mathrm{1}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{1}}{\mathrm{2}}=\mathrm{2}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{1}}{\mathrm{2}}=\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{h}} =\mathrm{ae}^{\mathrm{x}} \:+\mathrm{be}^{\mathrm{2x}} \:\:=\mathrm{au}_{\mathrm{1}} +\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\mathrm{2e}^{\mathrm{2x}} }\end{vmatrix}=\mathrm{2e}^{\mathrm{3x}} −\mathrm{e}^{\mathrm{3x}} \:=\mathrm{e}^{\mathrm{3x}} \:\neq\mathrm{0} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{2x}} }\\{\mathrm{e}^{\mathrm{4x}} \:\:\:\:\:\:\mathrm{2e}^{\mathrm{2x}} }\end{vmatrix}=−\mathrm{e}^{\mathrm{6x}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\mathrm{o}}\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{4x}} }\end{vmatrix}=\mathrm{e}^{\mathrm{5x}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{W}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{−\mathrm{e}^{\mathrm{6x}} }{\mathrm{e}^{\mathrm{3x}} }\mathrm{dx}\:=−\int\:\mathrm{e}^{\mathrm{3x}} \:\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\mathrm{3x}} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\frac{\mathrm{e}^{\mathrm{5x}} }{\mathrm{e}^{\mathrm{3x}} }\mathrm{dx}\:=\int\:\mathrm{e}^{\mathrm{2x}} \:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =\mathrm{e}^{\mathrm{x}} \left(−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\mathrm{3x}} \right)+\mathrm{e}^{\mathrm{2x}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \right)=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\mathrm{4x}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{4x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{e}^{\mathrm{4x}} \:\:\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=\mathrm{ae}^{\mathrm{x}} \:+\mathrm{be}^{\mathrm{2x}} \:+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{e}^{\mathrm{4x}} \\ $$$$\mathrm{y}\left(\mathrm{0}\right)=\mathrm{1}\:\Rightarrow\mathrm{a}+\mathrm{b}+\frac{\mathrm{1}}{\mathrm{6}}=\mathrm{1}\:\Rightarrow\mathrm{a}+\mathrm{b}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\mathrm{y}^{'} \left(\mathrm{x}\right)=\mathrm{ae}^{\mathrm{x}} \:+\mathrm{2b}\:\mathrm{e}^{\mathrm{2x}} \:+\frac{\mathrm{2}}{\mathrm{3}}\mathrm{e}^{\mathrm{4x}} \\ $$$$\mathrm{y}^{'} \left(\mathrm{o}\right)=\mathrm{0}\:\Rightarrow\mathrm{a}+\mathrm{2b}\:+\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{0}\:\Rightarrow\mathrm{a}+\mathrm{2b}=−\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{system} \\ $$$$\begin{cases}{\mathrm{a}+\mathrm{b}=\frac{\mathrm{5}}{\mathrm{6}}\:\:\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{b}=−\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{5}}{\mathrm{6}}=−\frac{\mathrm{9}}{\mathrm{6}}=−\frac{\mathrm{3}}{\mathrm{2}}}\\{\mathrm{a}+\mathrm{2b}=−\frac{\mathrm{2}}{\mathrm{3}}}\end{cases} \\ $$$$\mathrm{a}=\frac{\mathrm{5}}{\mathrm{6}}+\frac{\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{5}+\mathrm{9}}{\mathrm{6}}=\frac{\mathrm{14}}{\mathrm{6}}=\frac{\mathrm{7}}{\mathrm{3}}\:\Rightarrow\bigstar\mathrm{y}\left(\mathrm{x}\right)=\frac{\mathrm{7}}{\mathrm{3}}\mathrm{e}^{\mathrm{x}} −\frac{\mathrm{3}}{\mathrm{2}}\mathrm{e}^{\mathrm{2x}} \:+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{e}^{\mathrm{4x}} \:\:\bigstar \\ $$$$ \\ $$
