Menu Close

d-2sin-2-cos-2-

Tinku Tara 0 Comments
Pin




Question Number 102926 by mohammad17 last updated on 11/Jul/20
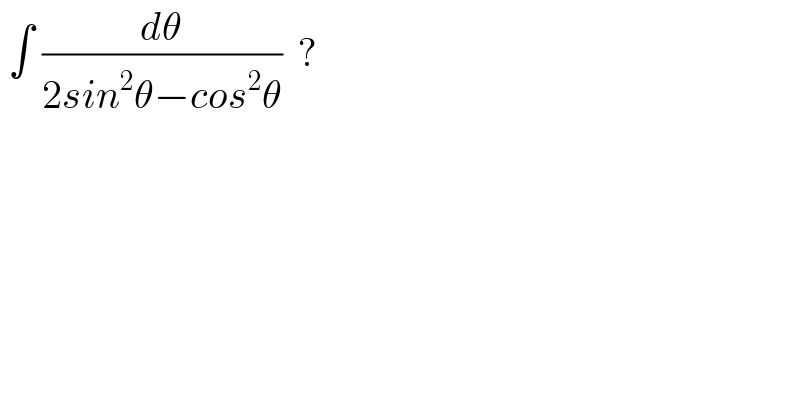
∫ (dθ/(2sin^2 θ−cos^2 θ)) ?
$$\:\int\:\frac{{d}\theta}{\mathrm{2}{sin}^{\mathrm{2}} \theta−{cos}^{\mathrm{2}} \theta}\:\:? \\ $$
Answered by OlafThorendsen last updated on 11/Jul/20
∫(dθ/(2((2t)/(1+t^2 ))−((1−t^2 )/(1+t^2 )))) (t = tan(θ/2)) ∫((1+t^2 )/(t^2 +4t−1))dθ ∫((1+t^2 )/((t+2)^2 −5))dθ ∫((1+t^2 )/(2(√5)))[(1/(t+2−(√5)))−(1/(t+2+(√5)))]dθ (1/( (√5)))ln((t+2−(√5))/(t+2+(√5)))+C (1/( (√5)))ln((tan(θ/2)+2−(√5))/(tan(θ/2)+2+(√5)))+C
$$\int\frac{{d}\theta}{\mathrm{2}\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$\left({t}\:=\:{tan}\frac{\theta}{\mathrm{2}}\right) \\ $$$$\int\frac{\mathrm{1}+{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{4}{t}−\mathrm{1}}{d}\theta \\ $$$$\int\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\left({t}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{5}}{d}\theta \\ $$$$\int\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{5}}}\left[\frac{\mathrm{1}}{{t}+\mathrm{2}−\sqrt{\mathrm{5}}}−\frac{\mathrm{1}}{{t}+\mathrm{2}+\sqrt{\mathrm{5}}}\right]{d}\theta \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\mathrm{ln}\frac{{t}+\mathrm{2}−\sqrt{\mathrm{5}}}{{t}+\mathrm{2}+\sqrt{\mathrm{5}}}+\mathrm{C} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\mathrm{ln}\frac{{tan}\frac{\theta}{\mathrm{2}}+\mathrm{2}−\sqrt{\mathrm{5}}}{{tan}\frac{\theta}{\mathrm{2}}+\mathrm{2}+\sqrt{\mathrm{5}}}+\mathrm{C} \\ $$
Commented by mohammad17 last updated on 11/Jul/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 11/Jul/20
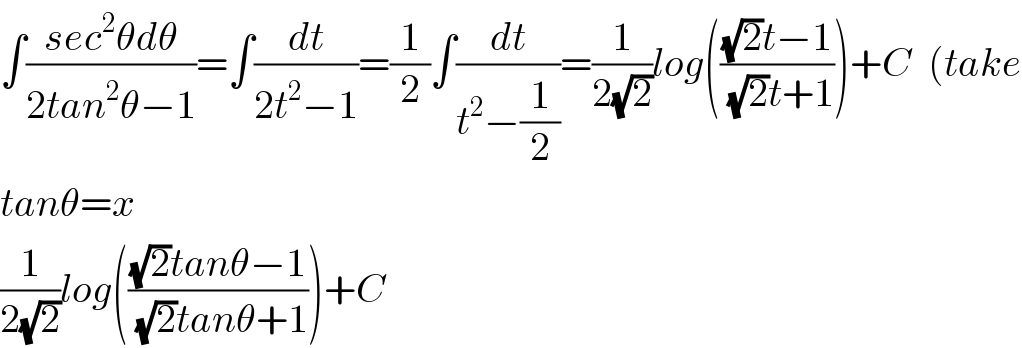
∫((sec^2 θdθ)/(2tan^2 θ−1))=∫(dt/(2t^2 −1))=(1/2)∫(dt/(t^2 −(1/2)))=(1/(2(√2)))log((((√2)t−1)/( (√2)t+1)))+C (take tanθ=x (1/(2(√2)))log((((√2)tanθ−1)/( (√2)tanθ+1)))+C
$$\int\frac{{sec}^{\mathrm{2}} \theta{d}\theta}{\mathrm{2}{tan}^{\mathrm{2}} \theta−\mathrm{1}}=\int\frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\left(\frac{\sqrt{\mathrm{2}}{t}−\mathrm{1}}{\:\sqrt{\mathrm{2}}{t}+\mathrm{1}}\right)+{C}\:\:\left({take}\right. \\ $$$${tan}\theta={x} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{log}\left(\frac{\sqrt{\mathrm{2}}{tan}\theta−\mathrm{1}}{\:\sqrt{\mathrm{2}}{tan}\theta+\mathrm{1}}\right)+{C} \\ $$
Commented by mohammad17 last updated on 11/Jul/20
very nice thank you sir
$${very}\:{nice}\:{thank}\:{you}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 11/Jul/20
I =∫ (dx/(2sin^2 x−cos^2 x)) ⇒ I =∫ (dx/(2sin^2 x−(1−sin^2 x))) =∫ (dx/(2sin^2 x−1+sin^2 x)) =∫ (dx/(3sin^2 x−1)) =∫ (dx/(((√3)sinx−1)((√3)sinx+1))) =(1/2)∫ ((1/( (√3)sinx−1))−(1/( (√3)sinx +1)))dx =H−K H =(1/2) ∫ (dx/( (√3)sinx −1)) ⇒2H =_(tan((x/2))=t) ∫ ((2dt)/((1+t^2 )((√3)×((2t)/(1+t^2 )) −1))) =∫ ((2dt)/(2(√3)t−1−t^2 )) =−2 ∫ (dt/(t^2 −2(√3)t +1)) t^2 −2(√3)t +1 =0 →Δ^′ =3−1=2 ⇒t_1 =(√3)+(√2) and t_2 =(√3)−(√2) 2H =−2 ∫ (dt/((t−t_1 )(t−t_2 ))) =((−1)/( (√2))) ∫((1/(t−t_1 ))−(1/(t−t_2 )))dt H=−(1/(2(√2)))ln∣((t−t_1 )/(t−t_2 ))∣ +C =−(1/(2(√2)))ln∣((tan((x/2))−(√3)−(√2))/(tan((x/2))−(√3)+(√2)))∣ +C K =(1/2)∫ (dx/( (√3)sinx +1)) ⇒2K =_(tan((x/2))=t) ∫ ((2dt)/((1+t^2 )((√3)×((2t)/(1+t^2 )) +1))) ⇒K =∫ (dt/(2(√3)t +1+t^2 )) =∫ (dt/(t^2 +2(√3)t +1)) Δ^′ =2 ⇒ t_1 =−(√3)+(√2) and t_2 =−(√3)−(√2) ⇒ K =∫ (dt/((t−t_1 )(t−t_2 ))) =(1/(2(√2)))∫((1/(t−t_1 ))−(1/(t−t_2 )))dt =(1/(2(√2)))ln∣((t−t_1 )/(t−t_2 ))∣ +C =(1/(2(√2)))ln∣((tan((x/2))+(√3)−(√2))/(tan((x/2))+(√3)+(√2)))∣ +C I =H−K
$$\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{2sin}^{\mathrm{2}} \mathrm{x}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow\:\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{2sin}^{\mathrm{2}} \mathrm{x}−\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)} \\ $$$$=\int\:\:\frac{\mathrm{dx}}{\mathrm{2sin}^{\mathrm{2}} \mathrm{x}−\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\:=\int\:\:\frac{\mathrm{dx}}{\mathrm{3sin}^{\mathrm{2}} \mathrm{x}−\mathrm{1}}\:=\int\:\:\frac{\mathrm{dx}}{\left(\sqrt{\mathrm{3}}\mathrm{sinx}−\mathrm{1}\right)\left(\sqrt{\mathrm{3}}\mathrm{sinx}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\mathrm{sinx}−\mathrm{1}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\mathrm{sinx}\:+\mathrm{1}}\right)\mathrm{dx}\:=\mathrm{H}−\mathrm{K} \\ $$$$\mathrm{H}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{3}}\mathrm{sinx}\:−\mathrm{1}}\:\Rightarrow\mathrm{2H}\:=_{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}} \:\:\:\:\int\:\:\:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\sqrt{\mathrm{3}}×\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:−\mathrm{1}\right)} \\ $$$$=\int\:\:\frac{\mathrm{2dt}}{\mathrm{2}\sqrt{\mathrm{3}}\mathrm{t}−\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\:=−\mathrm{2}\:\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}\mathrm{t}\:+\mathrm{1}} \\ $$$$\mathrm{t}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}\mathrm{t}\:+\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{3}−\mathrm{1}=\mathrm{2}\:\Rightarrow\mathrm{t}_{\mathrm{1}} =\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\:\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}} \\ $$$$\mathrm{2H}\:=−\mathrm{2}\:\int\:\:\frac{\mathrm{dt}}{\left(\mathrm{t}−\mathrm{t}_{\mathrm{1}} \right)\left(\mathrm{t}−\mathrm{t}_{\mathrm{2}} \right)}\:=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int\left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }\right)\mathrm{dt} \\ $$$$\mathrm{H}=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }\mid\:+\mathrm{C}\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}}{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}}\mid\:+\mathrm{C} \\ $$$$\mathrm{K}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{3}}\mathrm{sinx}\:+\mathrm{1}}\:\Rightarrow\mathrm{2K}\:=_{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}} \:\:\:\int\:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\sqrt{\mathrm{3}}×\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:+\mathrm{1}\right)} \\ $$$$\Rightarrow\mathrm{K}\:=\int\:\:\frac{\mathrm{dt}}{\mathrm{2}\sqrt{\mathrm{3}}\mathrm{t}\:+\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}\mathrm{t}\:+\mathrm{1}} \\ $$$$\Delta^{'} \:=\mathrm{2}\:\Rightarrow\:\mathrm{t}_{\mathrm{1}} =−\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\:\mathrm{and}\:\mathrm{t}_{\mathrm{2}} =−\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{K}\:=\int\:\frac{\mathrm{dt}}{\left(\mathrm{t}−\mathrm{t}_{\mathrm{1}} \right)\left(\mathrm{t}−\mathrm{t}_{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\int\left(\frac{\mathrm{1}}{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }\mid\:+\mathrm{C}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}}{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}}\mid\:+\mathrm{C} \\ $$$$\mathrm{I}\:=\mathrm{H}−\mathrm{K} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *