Question Number 56580 by subhankar10 last updated on 18/Mar/19
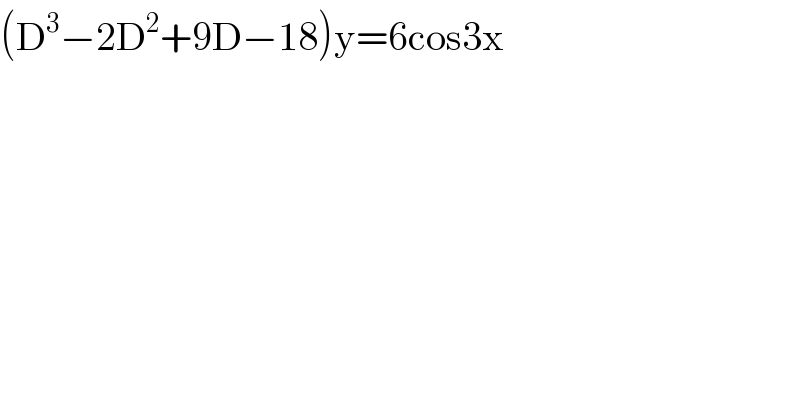
$$\left(\mathrm{D}^{\mathrm{3}} −\mathrm{2D}^{\mathrm{2}} +\mathrm{9D}−\mathrm{18}\right)\mathrm{y}=\mathrm{6cos3x} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Mar/19
![let y=e^(mx) be a solution Dy=me^(mx) D^2 y=m^2 e^(mx) .. so complimentary function m^3 e^(mx) −2m^2 e^(mx) +9me^(mx) −18e^(mx) =0 e^(mx) (m^3 −2m^2 +9m−18)=0 e^(mx) ≠0 m^3 −2m^2 +9m−18=0 m^2 (n−2)+9(m−2)=0 (m−2)(m^2 +9)=0 m=2 and ±3i C.F C_1 e^(2x) +C_2 e^(i3x) +C_3 e^(−i3x) Particular intregal y=((6cos3x)/(D^3 −2D^2 +9D−18)) =6×((cos3x)/(D^2 (D−2)+9(D−2))) =6×((cos3x)/((D−2)(D^2 +9))) =6×(((D+2) cos3x)/((D^2 −4)(D^2 +9))) =(6/((−3^2 −4)))×((−3sin3x+2cos3x)/(D^2 +9)) =((−6)/(13))×((−3sin3x+2cos3x)/(D^2 +9)) =(6/(13))×(((3sin3x−2cos3x))/(D^2 +9)) =(6/(13))×((rsin(3x−θ))/(D^2 +9)) [r=(√(3^2 +2^2 )) =(√(13)) tanθ=(2/3)] p=(6/( (√(13)) ))×((cos(3x−θ))/(D^2 +9)) q=(6/( (√(13))))×((sin(3x−θ))/(D^2 +9)) p+iq=(6/( (√(13))))×(e^(i(3x−θ)) /(D^2 +9)) p+iq=(6/( (√(13))))×e^(−iθ) ×(e^(i×3x) /(D^2 +9)) p+iq=(6/( (√(13))))×e^(−iθ) ×(e^(i3x) /((D+i3)(D−i3))) p+iq=(6/( (√(13))))×(cosθ−isinθ)×(e^(i3x) /((i3+i3)(D+i3−i3)))×1 =(6/( (√(13))))×((3/( (√(13))))−i×(2/( (√(13)))))×(((cos3x+isin3x))/(6i))×x =(1/(13))×((3i+2)/i^2 )×(xcos3x+ixsin3x) =((−1)/(13))(i3xcos3x−3xsin3x+2xcos3x+i2xsin3x) =((−1)/(13)){(2xcos3x−3xsin3x)+i(3xcos3x+2xsin3x)} =((−x)/(13))(2cos3x−3sin3x)+((−ix)/(13))(3cos3x+2sin3x) now our answer is related to complex part so answer is Particular intregal is =((−x)/(13))(3cos3x+2sin3x) so complte answer is=C.F+P.I y=C_1 e^(2x) +C_2 e^(i3x) +C_3 e^(−i3x) +((−x)/(13))(3cos3x+2sin3x)](https://www.tinkutara.com/question/Q56581.png)
$${let}\:{y}={e}^{{mx}} \:{be}\:{a}\:{solution} \\ $$$${Dy}={me}^{{mx}} \\ $$$${D}^{\mathrm{2}} {y}={m}^{\mathrm{2}} {e}^{{mx}} \\ $$$$.. \\ $$$${so} \\ $$$${complimentary}\:{function} \\ $$$$ \\ $$$${m}^{\mathrm{3}} {e}^{{mx}} −\mathrm{2}{m}^{\mathrm{2}} {e}^{{mx}} +\mathrm{9}{me}^{{mx}} −\mathrm{18}{e}^{{mx}} =\mathrm{0} \\ $$$${e}^{{mx}} \left({m}^{\mathrm{3}} −\mathrm{2}{m}^{\mathrm{2}} +\mathrm{9}{m}−\mathrm{18}\right)=\mathrm{0} \\ $$$${e}^{{mx}} \neq\mathrm{0} \\ $$$${m}^{\mathrm{3}} −\mathrm{2}{m}^{\mathrm{2}} +\mathrm{9}{m}−\mathrm{18}=\mathrm{0} \\ $$$${m}^{\mathrm{2}} \left({n}−\mathrm{2}\right)+\mathrm{9}\left({m}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\left({m}−\mathrm{2}\right)\left({m}^{\mathrm{2}} +\mathrm{9}\right)=\mathrm{0} \\ $$$${m}=\mathrm{2}\:{and}\:\:\pm\mathrm{3}{i} \\ $$$${C}.{F} \\ $$$${C}_{\mathrm{1}} {e}^{\mathrm{2}{x}} +{C}_{\mathrm{2}} {e}^{{i}\mathrm{3}{x}} +{C}_{\mathrm{3}} {e}^{−{i}\mathrm{3}{x}} \\ $$$${Particular}\:{intregal} \\ $$$${y}=\frac{\mathrm{6}{cos}\mathrm{3}{x}}{{D}^{\mathrm{3}} −\mathrm{2}{D}^{\mathrm{2}} +\mathrm{9}{D}−\mathrm{18}} \\ $$$$=\mathrm{6}×\frac{{cos}\mathrm{3}{x}}{{D}^{\mathrm{2}} \left({D}−\mathrm{2}\right)+\mathrm{9}\left({D}−\mathrm{2}\right)} \\ $$$$=\mathrm{6}×\frac{{cos}\mathrm{3}{x}}{\left({D}−\mathrm{2}\right)\left({D}^{\mathrm{2}} +\mathrm{9}\right)} \\ $$$$=\mathrm{6}×\frac{\left({D}+\mathrm{2}\right)\:{cos}\mathrm{3}{x}}{\left({D}^{\mathrm{2}} −\mathrm{4}\right)\left({D}^{\mathrm{2}} +\mathrm{9}\right)} \\ $$$$=\frac{\mathrm{6}}{\left(−\mathrm{3}^{\mathrm{2}} −\mathrm{4}\right)}×\frac{−\mathrm{3}{sin}\mathrm{3}{x}+\mathrm{2}{cos}\mathrm{3}{x}}{{D}^{\mathrm{2}} +\mathrm{9}} \\ $$$$=\frac{−\mathrm{6}}{\mathrm{13}}×\frac{−\mathrm{3}{sin}\mathrm{3}{x}+\mathrm{2}{cos}\mathrm{3}{x}}{{D}^{\mathrm{2}} +\mathrm{9}} \\ $$$$=\frac{\mathrm{6}}{\mathrm{13}}×\frac{\left(\mathrm{3}{sin}\mathrm{3}{x}−\mathrm{2}{cos}\mathrm{3}{x}\right)}{{D}^{\mathrm{2}} +\mathrm{9}} \\ $$$$=\frac{\mathrm{6}}{\mathrm{13}}×\frac{{rsin}\left(\mathrm{3}{x}−\theta\right)}{{D}^{\mathrm{2}} +\mathrm{9}}\:\left[{r}=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }\:=\sqrt{\mathrm{13}}\:\:\:{tan}\theta=\frac{\mathrm{2}}{\mathrm{3}}\right] \\ $$$${p}=\frac{\mathrm{6}}{\:\sqrt{\mathrm{13}}\:}×\frac{{cos}\left(\mathrm{3}{x}−\theta\right)}{{D}^{\mathrm{2}} +\mathrm{9}} \\ $$$${q}=\frac{\mathrm{6}}{\:\sqrt{\mathrm{13}}}×\frac{{sin}\left(\mathrm{3}{x}−\theta\right)}{{D}^{\mathrm{2}} +\mathrm{9}} \\ $$$${p}+{iq}=\frac{\mathrm{6}}{\:\sqrt{\mathrm{13}}}×\frac{{e}^{{i}\left(\mathrm{3}{x}−\theta\right)} }{{D}^{\mathrm{2}} +\mathrm{9}} \\ $$$${p}+{iq}=\frac{\mathrm{6}}{\:\sqrt{\mathrm{13}}}×{e}^{−{i}\theta} ×\frac{{e}^{{i}×\mathrm{3}{x}} }{{D}^{\mathrm{2}} +\mathrm{9}} \\ $$$${p}+{iq}=\frac{\mathrm{6}}{\:\sqrt{\mathrm{13}}}×{e}^{−{i}\theta} ×\frac{{e}^{{i}\mathrm{3}{x}} }{\left({D}+{i}\mathrm{3}\right)\left({D}−{i}\mathrm{3}\right)} \\ $$$${p}+{iq}=\frac{\mathrm{6}}{\:\sqrt{\mathrm{13}}}×\left({cos}\theta−{isin}\theta\right)×\frac{{e}^{{i}\mathrm{3}{x}} }{\left({i}\mathrm{3}+{i}\mathrm{3}\right)\left({D}+{i}\mathrm{3}−{i}\mathrm{3}\right)}×\mathrm{1} \\ $$$$=\frac{\mathrm{6}}{\:\sqrt{\mathrm{13}}}×\left(\frac{\mathrm{3}}{\:\sqrt{\mathrm{13}}}−{i}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}\right)×\frac{\left({cos}\mathrm{3}{x}+{isin}\mathrm{3}{x}\right)}{\mathrm{6}{i}}×{x} \\ $$$$=\frac{\mathrm{1}}{\mathrm{13}}×\frac{\mathrm{3}{i}+\mathrm{2}}{{i}^{\mathrm{2}} }×\left({xcos}\mathrm{3}{x}+{ixsin}\mathrm{3}{x}\right) \\ $$$$=\frac{−\mathrm{1}}{\mathrm{13}}\left({i}\mathrm{3}{xcos}\mathrm{3}{x}−\mathrm{3}{xsin}\mathrm{3}{x}+\mathrm{2}{xcos}\mathrm{3}{x}+{i}\mathrm{2}{xsin}\mathrm{3}{x}\right) \\ $$$$=\frac{−\mathrm{1}}{\mathrm{13}}\left\{\left(\mathrm{2}{xcos}\mathrm{3}{x}−\mathrm{3}{xsin}\mathrm{3}{x}\right)+{i}\left(\mathrm{3}{xcos}\mathrm{3}{x}+\mathrm{2}{xsin}\mathrm{3}{x}\right)\right\} \\ $$$$=\frac{−{x}}{\mathrm{13}}\left(\mathrm{2}{cos}\mathrm{3}{x}−\mathrm{3}{sin}\mathrm{3}{x}\right)+\frac{−{ix}}{\mathrm{13}}\left(\mathrm{3}{cos}\mathrm{3}{x}+\mathrm{2}{sin}\mathrm{3}{x}\right) \\ $$$${now}\:{our}\:{answer}\:{is}\:{related}\:{to}\:{complex}\:{part} \\ $$$${so}\:{answer}\:{is} \\ $$$${Particular}\:{intregal}\:{is} \\ $$$$=\frac{−{x}}{\mathrm{13}}\left(\mathrm{3}{cos}\mathrm{3}{x}+\mathrm{2}{sin}\mathrm{3}{x}\right) \\ $$$${so}\:{complte}\:{answer}\:{is}={C}.{F}+{P}.{I} \\ $$$${y}={C}_{\mathrm{1}} {e}^{\mathrm{2}{x}} +{C}_{\mathrm{2}} {e}^{{i}\mathrm{3}{x}} +{C}_{\mathrm{3}} {e}^{−{i}\mathrm{3}{x}} +\frac{−{x}}{\mathrm{13}}\left(\mathrm{3}{cos}\mathrm{3}{x}+\mathrm{2}{sin}\mathrm{3}{x}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
