Menu Close

D-3-5D-2-7D-3-y-e-2x-cosh-x-

Tinku Tara 0 Comments
Pin




Question Number 127291 by bemath last updated on 28/Dec/20
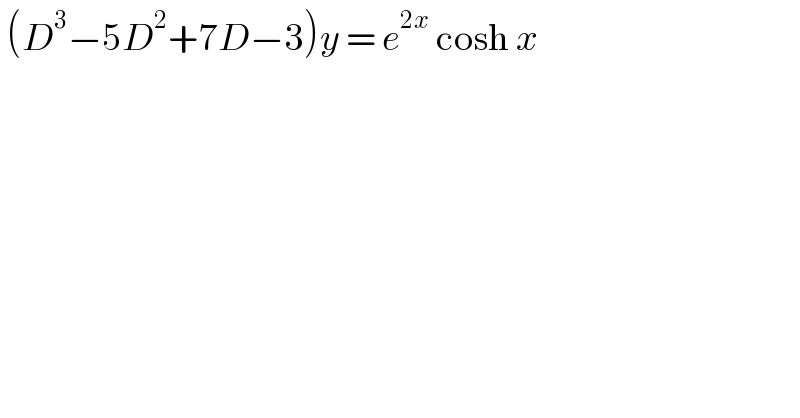
(D^3 −5D^2 +7D−3)y = e^(2x) cosh x
$$\:\left({D}^{\mathrm{3}} −\mathrm{5}{D}^{\mathrm{2}} +\mathrm{7}{D}−\mathrm{3}\right){y}\:=\:{e}^{\mathrm{2}{x}} \:\mathrm{cosh}\:{x} \\ $$
Answered by liberty last updated on 28/Dec/20
note that e^(2x) cosh x = ((e^(3x) +e^x )/2) the diff eq becomes (D^3 −5D^2 +7D−3)y = ((e^(3x) +e^x )/2) the homogenous particular of eq i.e ⇒f′′′−5f′′+7f′−3=0 take y = V(x)f(x) and substitute in the eq we get V′′′−2V′′ = (1/2)e^x +(1/2) this can be integrated twice to produce the first order V′−2V=(1/8)e^(2x) +x^2 +C_1 x+C_2 the solution given by V=e^(2x) [∫e^(−2x) ((1/8)e^(2x) +x^2 +C_1 x+C_2 )dx+C_3 ] V=(1/8)xe^(2x) +C_3 e^(2x) −(1/2)x^2 −Ax−B where A=((C_1 +1)/2) ; B=((C_1 +2C_2 +1)/4) y = (C_3 +(1/8)x)e^(3x) −(Ax+(1/2)x^2 +B)e^x .
$$\:{note}\:{that}\:{e}^{\mathrm{2}{x}} \:\mathrm{cosh}\:{x}\:=\:\frac{{e}^{\mathrm{3}{x}} +{e}^{{x}} }{\mathrm{2}} \\ $$$${the}\:{diff}\:{eq}\:{becomes}\: \\ $$$$\left({D}^{\mathrm{3}} −\mathrm{5}{D}^{\mathrm{2}} +\mathrm{7}{D}−\mathrm{3}\right){y}\:=\:\frac{{e}^{\mathrm{3}{x}} +{e}^{{x}} }{\mathrm{2}}\: \\ $$$${the}\:{homogenous}\:{particular}\:{of}\:{eq}\:{i}.{e} \\ $$$$\Rightarrow{f}'''−\mathrm{5}{f}''+\mathrm{7}{f}'−\mathrm{3}=\mathrm{0}\: \\ $$$${take}\:{y}\:=\:{V}\left({x}\right){f}\left({x}\right)\:{and}\:{substitute}\:{in}\:{the} \\ $$$${eq}\:{we}\:{get}\:{V}'''−\mathrm{2}{V}''\:=\:\frac{\mathrm{1}}{\mathrm{2}}{e}^{{x}} +\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${this}\:{can}\:{be}\:{integrated}\:{twice}\:{to}\:{produce} \\ $$$${the}\:{first}\:{order}\:{V}'−\mathrm{2}{V}=\frac{\mathrm{1}}{\mathrm{8}}{e}^{\mathrm{2}{x}} +{x}^{\mathrm{2}} +{C}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} \\ $$$${the}\:{solution}\:{given}\:{by} \\ $$$${V}={e}^{\mathrm{2}{x}} \:\left[\int{e}^{−\mathrm{2}{x}} \left(\frac{\mathrm{1}}{\mathrm{8}}{e}^{\mathrm{2}{x}} +{x}^{\mathrm{2}} +{C}_{\mathrm{1}} {x}+{C}_{\mathrm{2}} \right){dx}+{C}_{\mathrm{3}} \:\right] \\ $$$${V}=\frac{\mathrm{1}}{\mathrm{8}}{xe}^{\mathrm{2}{x}} +{C}_{\mathrm{3}} {e}^{\mathrm{2}{x}} −\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −{Ax}−{B}\: \\ $$$${where}\:{A}=\frac{{C}_{\mathrm{1}} +\mathrm{1}}{\mathrm{2}}\:;\:{B}=\frac{{C}_{\mathrm{1}} +\mathrm{2}{C}_{\mathrm{2}} +\mathrm{1}}{\mathrm{4}} \\ $$$$\:{y}\:=\:\left({C}_{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{8}}{x}\right){e}^{\mathrm{3}{x}} −\left({Ax}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{B}\right){e}^{{x}} .\: \\ $$
Answered by bemath last updated on 28/Dec/20
Characteristic equation r^3 −5r^2 +7r−3=0 has the roots r=1,1,2 homogenous solution y_h = (Ax+B)e^x +Ce^(3x) particular solution y_p = ax^2 e^x +bxe^(3x) we get { ((−8a=1⇒a=−(1/8))),((8b=1⇒b=(1/8))) :} so particular solution is y_p = −(1/8)x^2 e^x +(1/8)xe^(3x) general solution is y_g = (Ax+B)e^x +Ce^(3x) −(1/8)x^2 e^x +(1/8)xe^(3x)
$${Characteristic}\:{equation}\: \\ $$$${r}^{\mathrm{3}} −\mathrm{5}{r}^{\mathrm{2}} +\mathrm{7}{r}−\mathrm{3}=\mathrm{0} \\ $$$${has}\:{the}\:{roots}\:{r}=\mathrm{1},\mathrm{1},\mathrm{2} \\ $$$${homogenous}\:{solution}\: \\ $$$${y}_{{h}} \:=\:\left({Ax}+{B}\right){e}^{{x}} +{Ce}^{\mathrm{3}{x}} \\ $$$$ \\ $$$${particular}\:{solution}\: \\ $$$${y}_{{p}} =\:{ax}^{\mathrm{2}} {e}^{{x}} +{bxe}^{\mathrm{3}{x}} \\ $$$${we}\:{get}\:\begin{cases}{−\mathrm{8}{a}=\mathrm{1}\Rightarrow{a}=−\frac{\mathrm{1}}{\mathrm{8}}}\\{\mathrm{8}{b}=\mathrm{1}\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{8}}}\end{cases} \\ $$$${so}\:{particular}\:{solution}\:{is}\: \\ $$$${y}_{{p}} =\:−\frac{\mathrm{1}}{\mathrm{8}}{x}^{\mathrm{2}} {e}^{{x}} +\frac{\mathrm{1}}{\mathrm{8}}{xe}^{\mathrm{3}{x}} \\ $$$$ \\ $$$${general}\:{solution}\:{is}\: \\ $$$${y}_{{g}} \:=\:\left({Ax}+{B}\right){e}^{{x}} +{Ce}^{\mathrm{3}{x}} −\frac{\mathrm{1}}{\mathrm{8}}{x}^{\mathrm{2}} {e}^{{x}} +\frac{\mathrm{1}}{\mathrm{8}}{xe}^{\mathrm{3}{x}} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 29/Dec/20
y^((3)) −5y^((2)) +7y^((1)) −3y =e^(2x) ×((e^x +e^(−x) )/2)=((e^(3x) +e^x )/2) h→p(r)=r^3 −5r^2 +7r−3=0 ,1 is root p^′ (r)=3r^2 −10r+7 ⇒p^′ (1)=0 ⇒1 is double root ⇒p(r)=(r−1)^2 Q(r)=(r−1)^2 (r+a) ⇒a=3 ⇒y_h =(αx+β)e^x +c e^(3x) =αxe^x +βe^x +c e^(3x) =αu_1 +βu_2 +cu_3 w(u_1 ,u_2 ,u_3 ) = determinant (((xe^x e^x e^(3x) )),(((x+1)e^x e^x 3e^(3x) ))) ∣(x+2)e^x e^x 9e^(3x) ∣ =xe^x determinant (((e^x 3e^(3x) )),((e^x 9e^(3x) )))−(x+1)e^x determinant (((e^x e^(3x) )),((e^x 9e^(3x) )))+(x+2)e^x determinant (((e^(x ) e^(3x) )),((e^x 3e^(3x) ))) =xe^x (9e^(4x) −3e^(4x) )−(x+1)e^x (9e^(4x) −e^(4x) )+(x+2)e^x (3e^(4x) −e^(4x) ) =xe^x )6e^(4x) −(x+1)e^x )8e^(4x) +(x+2)e^x (2e^(4x) ) =6x e^(5x) −8(x+1)e^(5x) +2(x+2)e^(5x) =(6x−8x−8+2x+4)e^(5x) =−4e^(5x) w_1 = determinant (((o e^x e^(3x) )),((o e^x 3e^(3x) )))=((e^(3x) +e^x )/2)× determinant (((e^x e^(3x) )),((e^x 3e^(3x) )))=((e^(3x) +e^x )/2)(2e^(4x) ) ∣((e^(3x) +e^x )/(2 )) e^(x ) 9e^(3x) ∣=e^(7x) +e^(5x) w_2 = determinant (((xe^x 0 e^(3x) )),(((x+1)e^x 0 3e^(3x) )))=xe^x determinant (((o 3e^(3x) )),((((e^(3x) +e^x )/2) 9e^(3x) )))−(x+1)e^x determinant (((o e^(3x) )),((((e^(3x) +e^x )/2) 9e^(3x) ))) ∣ (x+2)e^x ((e^(3x) +e^x )/(2 )) 9e^(3x) ∣ +(x+2) determinant (((o e^(3x) )),((0 3e^(3x) )))=xe^x (−(3/2))(e^(6x) +e^(4x) )−(x+1)e^x ×(1/2)(e^(6x) +e^(4x) ) =.... w_3 = determinant (((xe^x e^x 0)),(((x+1)e^x e^x 0))) ∣ (x+2)e^x e^x ((e^(3x) +e^x )/2)∣=....(rest calculus) v_1 =∫ (w_1 /w)dx =.... v_2 =∫ (w_2 /w)dx=... v_3 =∫ (w_3 /w)dx=... ⇒y_p =u_1 v_1 +u_2 v_2 +u_3 v_3 general solution is y =y_h +y_p
$$\mathrm{y}^{\left(\mathrm{3}\right)} −\mathrm{5y}^{\left(\mathrm{2}\right)} \:+\mathrm{7y}^{\left(\mathrm{1}\right)} −\mathrm{3y}\:=\mathrm{e}^{\mathrm{2x}} \:×\frac{\mathrm{e}^{\mathrm{x}} \:+\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}=\frac{\mathrm{e}^{\mathrm{3x}} \:+\mathrm{e}^{\mathrm{x}} }{\mathrm{2}} \\ $$$$\mathrm{h}\rightarrow\mathrm{p}\left(\mathrm{r}\right)=\mathrm{r}^{\mathrm{3}} −\mathrm{5r}^{\mathrm{2}} \:+\mathrm{7r}−\mathrm{3}=\mathrm{0}\:\:\:,\mathrm{1}\:\mathrm{is}\:\mathrm{root}\:\: \\ $$$$\mathrm{p}^{'} \left(\mathrm{r}\right)=\mathrm{3r}^{\mathrm{2}} −\mathrm{10r}+\mathrm{7}\:\Rightarrow\mathrm{p}^{'} \left(\mathrm{1}\right)=\mathrm{0}\:\Rightarrow\mathrm{1}\:\mathrm{is}\:\mathrm{double}\:\mathrm{root} \\ $$$$\Rightarrow\mathrm{p}\left(\mathrm{r}\right)=\left(\mathrm{r}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{Q}\left(\mathrm{r}\right)=\left(\mathrm{r}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{r}+\mathrm{a}\right)\:\Rightarrow\mathrm{a}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{y}_{\mathrm{h}} =\left(\alpha\mathrm{x}+\beta\right)\mathrm{e}^{\mathrm{x}} \:+\mathrm{c}\:\mathrm{e}^{\mathrm{3x}} \:=\alpha\mathrm{xe}^{\mathrm{x}} \:+\beta\mathrm{e}^{\mathrm{x}} \:+\mathrm{c}\:\mathrm{e}^{\mathrm{3x}} \:=\alpha\mathrm{u}_{\mathrm{1}} \:+\beta\mathrm{u}_{\mathrm{2}} \:+\mathrm{cu}_{\mathrm{3}} \\ $$$$\mathrm{w}\left(\mathrm{u}_{\mathrm{1}} ,\mathrm{u}_{\mathrm{2}} ,\mathrm{u}_{\mathrm{3}} \right)\:=\begin{vmatrix}{\mathrm{xe}^{\mathrm{x}} \:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{3x}} }\\{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \:\:\mathrm{e}^{\mathrm{x}} \:\:\:\:\mathrm{3e}^{\mathrm{3x}} }\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\left(\mathrm{x}+\mathrm{2}\right)\mathrm{e}^{\mathrm{x}} \:\:\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\mathrm{9e}^{\mathrm{3x}} \:\mid \\ $$$$=\mathrm{xe}^{\mathrm{x}} \begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\mathrm{3e}^{\mathrm{3x}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\mathrm{9e}^{\mathrm{3x}} }\end{vmatrix}−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\mathrm{e}^{\mathrm{3x}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\mathrm{9e}^{\mathrm{3x}} }\end{vmatrix}+\left(\mathrm{x}+\mathrm{2}\right)\mathrm{e}^{\mathrm{x}} \begin{vmatrix}{\mathrm{e}^{\mathrm{x}\:\:\:\:\:} \:\:\:\mathrm{e}^{\mathrm{3x}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\mathrm{3e}^{\mathrm{3x}} }\end{vmatrix} \\ $$$$=\mathrm{xe}^{\mathrm{x}} \left(\mathrm{9e}^{\mathrm{4x}} −\mathrm{3e}^{\mathrm{4x}} \right)−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \left(\mathrm{9e}^{\mathrm{4x}} −\mathrm{e}^{\mathrm{4x}} \right)+\left(\mathrm{x}+\mathrm{2}\right)\mathrm{e}^{\mathrm{x}} \left(\mathrm{3e}^{\mathrm{4x}} −\mathrm{e}^{\mathrm{4x}} \right) \\ $$$$\left.=\left.\mathrm{xe}^{\mathrm{x}} \right)\mathrm{6e}^{\mathrm{4x}} −\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \right)\mathrm{8e}^{\mathrm{4x}} \:+\left(\mathrm{x}+\mathrm{2}\right)\mathrm{e}^{\mathrm{x}} \left(\mathrm{2e}^{\mathrm{4x}} \right) \\ $$$$=\mathrm{6x}\:\mathrm{e}^{\mathrm{5x}} −\mathrm{8}\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{5x}} +\mathrm{2}\left(\mathrm{x}+\mathrm{2}\right)\mathrm{e}^{\mathrm{5x}} \\ $$$$=\left(\mathrm{6x}−\mathrm{8x}−\mathrm{8}+\mathrm{2x}+\mathrm{4}\right)\mathrm{e}^{\mathrm{5x}} \:=−\mathrm{4e}^{\mathrm{5x}} \\ $$$$\mathrm{w}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\mathrm{e}^{\mathrm{3x}} }\\{\mathrm{o}\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\mathrm{3e}^{\mathrm{3x}} }\end{vmatrix}=\frac{\mathrm{e}^{\mathrm{3x}} \:+\mathrm{e}^{\mathrm{x}} }{\mathrm{2}}×\begin{vmatrix}{\mathrm{e}^{\mathrm{x}} \:\:\:\mathrm{e}^{\mathrm{3x}} }\\{\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\mathrm{3e}^{\mathrm{3x}} }\end{vmatrix}=\frac{\mathrm{e}^{\mathrm{3x}} \:+\mathrm{e}^{\mathrm{x}} }{\mathrm{2}}\left(\mathrm{2e}^{\mathrm{4x}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mid\frac{\mathrm{e}^{\mathrm{3x}} \:+\mathrm{e}^{\mathrm{x}} }{\mathrm{2}\:\:\:\:\:}\:\mathrm{e}^{\mathrm{x}\:\:\:} \:\mathrm{9e}^{\mathrm{3x}} \mid=\mathrm{e}^{\mathrm{7x}} \:+\mathrm{e}^{\mathrm{5x}} \\ $$$$\mathrm{w}_{\mathrm{2}} =\:\begin{vmatrix}{\mathrm{xe}^{\mathrm{x}} \:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{3x}} }\\{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \:\mathrm{0}\:\:\:\:\mathrm{3e}^{\mathrm{3x}} }\end{vmatrix}=\mathrm{xe}^{\mathrm{x}} \begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\mathrm{3e}^{\mathrm{3x}} }\\{\frac{\mathrm{e}^{\mathrm{3x}} \:+\mathrm{e}^{\mathrm{x}} }{\mathrm{2}}\:\:\:\mathrm{9e}^{\mathrm{3x}} }\end{vmatrix}−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \begin{vmatrix}{\mathrm{o}\:\:\:\:\:\:\mathrm{e}^{\mathrm{3x}} }\\{\frac{\mathrm{e}^{\mathrm{3x}} \:+\mathrm{e}^{\mathrm{x}} }{\mathrm{2}}\:\:\mathrm{9e}^{\mathrm{3x}} }\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\left(\mathrm{x}+\mathrm{2}\right)\mathrm{e}^{\mathrm{x}} \:\:\:\frac{\mathrm{e}^{\mathrm{3x}} +\mathrm{e}^{\mathrm{x}} }{\mathrm{2}\:\:\:}\:\:\:\:\mathrm{9e}^{\mathrm{3x}} \mid \\ $$$$+\left(\mathrm{x}+\mathrm{2}\right)\begin{vmatrix}{\mathrm{o}\:\:\:\:\:\mathrm{e}^{\mathrm{3x}} }\\{\mathrm{0}\:\:\:\:\:\:\mathrm{3e}^{\mathrm{3x}} }\end{vmatrix}=\mathrm{xe}^{\mathrm{x}} \left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\left(\mathrm{e}^{\mathrm{6x}} \:+\mathrm{e}^{\mathrm{4x}} \right)−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} ×\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{e}^{\mathrm{6x}} \:+\mathrm{e}^{\mathrm{4x}} \right) \\ $$$$=…. \\ $$$$\mathrm{w}_{\mathrm{3}} =\begin{vmatrix}{\mathrm{xe}^{\mathrm{x}} \:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \:\:\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\:\:\mathrm{0}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mid\:\left(\mathrm{x}+\mathrm{2}\right)\mathrm{e}^{\mathrm{x}} \:\:\:\:\mathrm{e}^{\mathrm{x}} \:\:\:\:\:\frac{\mathrm{e}^{\mathrm{3x}} +\mathrm{e}^{\mathrm{x}} }{\mathrm{2}}\mid=….\left(\mathrm{rest}\:\mathrm{calculus}\right) \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=…. \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}=… \\ $$$$\mathrm{v}_{\mathrm{3}} =\int\:\frac{\mathrm{w}_{\mathrm{3}} }{\mathrm{w}}\mathrm{dx}=…\:\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} +\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} +\mathrm{u}_{\mathrm{3}} \mathrm{v}_{\mathrm{3}} \\ $$$$\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *