Question Number 119235 by bemath last updated on 23/Oct/20
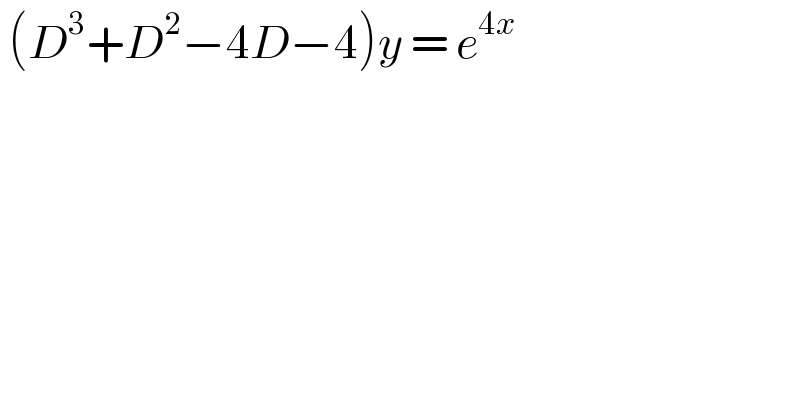
$$\:\left({D}^{\mathrm{3}} +{D}^{\mathrm{2}} −\mathrm{4}{D}−\mathrm{4}\right){y}\:=\:{e}^{\mathrm{4}{x}} \\ $$
Answered by benjo_mathlover last updated on 23/Oct/20
![(D+I)(D−2I)(D+2I)(y) = e^(4x) let (D−2I)(D+2I)(y) = z ⇒(D+I)(z) = e^(4x) ⇒ z′ +z = e^(4x) ; e^x (z′+z) = e^(5x) ⇒(e^x .z)′ = e^(5x) ; e^x .z = (1/5)e^(5x) +A ⇒z = (1/5)e^(4x) +Ae^(−x) ⇔ (D−2I)(D+2I)(y)=(1/5)e^(4x) +Ae^(−x) let (D+2I)(y) = q ⇒(D−2I)(q) = (1/5)e^(4x) +Ae^(−x) ⇒q′−2q = (1/5)e^(4x) +Ae^(−x) ⇒e^(−2x) (q′−2q) = (1/5)e^(2x) +Ae^(−3x) ⇒(e^(−2x) .q)′ = (1/5)e^(2x) +Ae^(−3x) ⇒ e^(−2x) .q = ∫ ((1/5)e^(2x) +Ae^(−3x) )dx ⇒q = (1/(10))e^(4x) −(1/3)Ae^(−x) +Be^(2x) ⇒(D+2I)(y) = (1/(10))e^(4x) −(1/3)Ae^(−x) +Be^(2x) ⇒e^(2x) (y′+2y) = (1/(10))e^(6x) −(1/3)Ae^x +Be^(4x) ⇒(e^(2x) .y)′ = (1/(10))e^(6x) −(1/3)Ae^x +Be^(4x) ⇒e^(2x) .y = ∫ ((1/(10))e^(6x) −(1/3)Ae^x +Be^(4x) ) dx ⇒y = (1/(60))e^(4x) −(1/3)Ae^(−x) +(1/4)Be^(2x) + Ce^(−2x) [ −(1/3)A=λ_1 , (1/4)B=λ_2 , C = λ_3 ] ∵ y = (1/(60))e^(4x) +λ_1 e^(−x) +λ_2 e^(2x) +λ_3 e^(−2x)](https://www.tinkutara.com/question/Q119237.png)
$$\left({D}+{I}\right)\left({D}−\mathrm{2}{I}\right)\left({D}+\mathrm{2}{I}\right)\left({y}\right)\:=\:{e}^{\mathrm{4}{x}} \\ $$$${let}\:\left({D}−\mathrm{2}{I}\right)\left({D}+\mathrm{2}{I}\right)\left({y}\right)\:=\:{z} \\ $$$$\Rightarrow\left({D}+{I}\right)\left({z}\right)\:=\:{e}^{\mathrm{4}{x}} \\ $$$$\Rightarrow\:{z}'\:+{z}\:=\:{e}^{\mathrm{4}{x}} \:;\:{e}^{{x}} \left({z}'+{z}\right)\:=\:{e}^{\mathrm{5}{x}} \\ $$$$\Rightarrow\left({e}^{{x}} .{z}\right)'\:=\:{e}^{\mathrm{5}{x}} \:;\:{e}^{{x}} .{z}\:=\:\frac{\mathrm{1}}{\mathrm{5}}{e}^{\mathrm{5}{x}} +{A} \\ $$$$\Rightarrow{z}\:=\:\frac{\mathrm{1}}{\mathrm{5}}{e}^{\mathrm{4}{x}} +{Ae}^{−{x}} \\ $$$$\Leftrightarrow\:\left({D}−\mathrm{2}{I}\right)\left({D}+\mathrm{2}{I}\right)\left({y}\right)=\frac{\mathrm{1}}{\mathrm{5}}{e}^{\mathrm{4}{x}} +{Ae}^{−{x}} \\ $$$${let}\:\left({D}+\mathrm{2}{I}\right)\left({y}\right)\:=\:{q}\: \\ $$$$\Rightarrow\left({D}−\mathrm{2}{I}\right)\left({q}\right)\:=\:\frac{\mathrm{1}}{\mathrm{5}}{e}^{\mathrm{4}{x}} +{Ae}^{−{x}} \\ $$$$\Rightarrow{q}'−\mathrm{2}{q}\:=\:\frac{\mathrm{1}}{\mathrm{5}}{e}^{\mathrm{4}{x}} +{Ae}^{−{x}} \\ $$$$\Rightarrow{e}^{−\mathrm{2}{x}} \left({q}'−\mathrm{2}{q}\right)\:=\:\frac{\mathrm{1}}{\mathrm{5}}{e}^{\mathrm{2}{x}} +{Ae}^{−\mathrm{3}{x}} \\ $$$$\Rightarrow\left({e}^{−\mathrm{2}{x}} .{q}\right)'\:=\:\frac{\mathrm{1}}{\mathrm{5}}{e}^{\mathrm{2}{x}} +{Ae}^{−\mathrm{3}{x}} \\ $$$$\Rightarrow\:{e}^{−\mathrm{2}{x}} .{q}\:=\:\int\:\left(\frac{\mathrm{1}}{\mathrm{5}}{e}^{\mathrm{2}{x}} +{Ae}^{−\mathrm{3}{x}} \:\right){dx} \\ $$$$\Rightarrow{q}\:=\:\frac{\mathrm{1}}{\mathrm{10}}{e}^{\mathrm{4}{x}} −\frac{\mathrm{1}}{\mathrm{3}}{Ae}^{−{x}} +{Be}^{\mathrm{2}{x}} \\ $$$$\Rightarrow\left({D}+\mathrm{2}{I}\right)\left({y}\right)\:=\:\frac{\mathrm{1}}{\mathrm{10}}{e}^{\mathrm{4}{x}} −\frac{\mathrm{1}}{\mathrm{3}}{Ae}^{−{x}} +{Be}^{\mathrm{2}{x}} \\ $$$$\Rightarrow{e}^{\mathrm{2}{x}} \left({y}'+\mathrm{2}{y}\right)\:=\:\frac{\mathrm{1}}{\mathrm{10}}{e}^{\mathrm{6}{x}} −\frac{\mathrm{1}}{\mathrm{3}}{Ae}^{{x}} +{Be}^{\mathrm{4}{x}} \\ $$$$\Rightarrow\left({e}^{\mathrm{2}{x}} .{y}\right)'\:=\:\frac{\mathrm{1}}{\mathrm{10}}{e}^{\mathrm{6}{x}} −\frac{\mathrm{1}}{\mathrm{3}}{Ae}^{{x}} +{Be}^{\mathrm{4}{x}} \\ $$$$\Rightarrow{e}^{\mathrm{2}{x}} .{y}\:=\:\int\:\left(\frac{\mathrm{1}}{\mathrm{10}}{e}^{\mathrm{6}{x}} −\frac{\mathrm{1}}{\mathrm{3}}{Ae}^{{x}} +{Be}^{\mathrm{4}{x}} \right)\:{dx} \\ $$$$\Rightarrow{y}\:=\:\frac{\mathrm{1}}{\mathrm{60}}{e}^{\mathrm{4}{x}} −\frac{\mathrm{1}}{\mathrm{3}}{Ae}^{−{x}} +\frac{\mathrm{1}}{\mathrm{4}}{Be}^{\mathrm{2}{x}} +\:{Ce}^{−\mathrm{2}{x}} \: \\ $$$$\left[\:−\frac{\mathrm{1}}{\mathrm{3}}{A}=\lambda_{\mathrm{1}} \:,\:\frac{\mathrm{1}}{\mathrm{4}}{B}=\lambda_{\mathrm{2}} \:,\:{C}\:=\:\lambda_{\mathrm{3}} \:\right]\: \\ $$$$\because\:{y}\:=\:\frac{\mathrm{1}}{\mathrm{60}}{e}^{\mathrm{4}{x}} +\lambda_{\mathrm{1}} {e}^{−{x}} +\lambda_{\mathrm{2}} {e}^{\mathrm{2}{x}} +\lambda_{\mathrm{3}} {e}^{−\mathrm{2}{x}} \\ $$
Commented by bemath last updated on 23/Oct/20

$${nice}… \\ $$
