Menu Close

D-3-D-2-y-x-2-1-y-0-1-y-0-1-y-0-0-

Tinku Tara 0 Comments
Pin




Question Number 87789 by john santu last updated on 06/Apr/20
(D^3 −D^2 )y = x^2 +1 ,y(0)=1 y ′(0)=−1 ,y ′′(0) = 0
$$\left(\mathrm{D}^{\mathrm{3}} −\mathrm{D}^{\mathrm{2}} \right)\mathrm{y}\:=\:\mathrm{x}^{\mathrm{2}} +\mathrm{1}\:,\mathrm{y}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\mathrm{y}\:'\left(\mathrm{0}\right)=−\mathrm{1}\:,\mathrm{y}\:''\left(\mathrm{0}\right)\:=\:\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 06/Apr/20
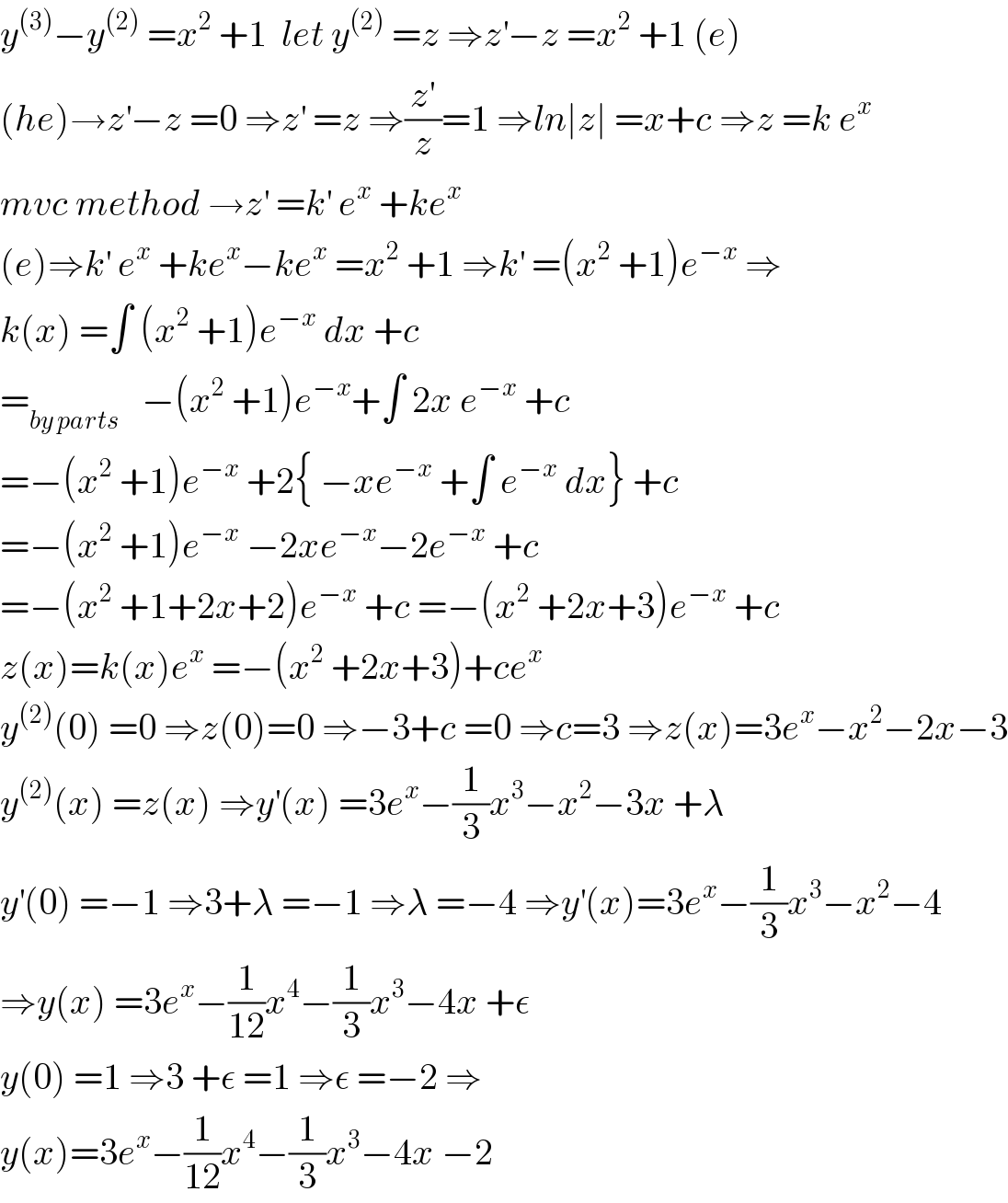
y^((3)) −y^((2)) =x^2 +1 let y^((2)) =z ⇒z^′ −z =x^2 +1 (e) (he)→z^′ −z =0 ⇒z^′ =z ⇒(z^′ /z)=1 ⇒ln∣z∣ =x+c ⇒z =k e^x mvc method →z^′ =k^′ e^x +ke^x (e)⇒k^′ e^x +ke^x −ke^x =x^2 +1 ⇒k^′ =(x^2 +1)e^(−x) ⇒ k(x) =∫ (x^2 +1)e^(−x) dx +c =_(by parts) −(x^2 +1)e^(−x) +∫ 2x e^(−x) +c =−(x^2 +1)e^(−x) +2{ −xe^(−x) +∫ e^(−x) dx} +c =−(x^2 +1)e^(−x) −2xe^(−x) −2e^(−x) +c =−(x^2 +1+2x+2)e^(−x) +c =−(x^2 +2x+3)e^(−x) +c z(x)=k(x)e^x =−(x^2 +2x+3)+ce^x y^((2)) (0) =0 ⇒z(0)=0 ⇒−3+c =0 ⇒c=3 ⇒z(x)=3e^x −x^2 −2x−3 y^((2)) (x) =z(x) ⇒y^′ (x) =3e^x −(1/3)x^3 −x^2 −3x +λ y^′ (0) =−1 ⇒3+λ =−1 ⇒λ =−4 ⇒y^′ (x)=3e^x −(1/3)x^3 −x^2 −4 ⇒y(x) =3e^x −(1/(12))x^4 −(1/3)x^3 −4x +ε y(0) =1 ⇒3 +ε =1 ⇒ε =−2 ⇒ y(x)=3e^x −(1/(12))x^4 −(1/3)x^3 −4x −2
$${y}^{\left(\mathrm{3}\right)} −{y}^{\left(\mathrm{2}\right)} \:={x}^{\mathrm{2}} \:+\mathrm{1}\:\:{let}\:{y}^{\left(\mathrm{2}\right)} \:={z}\:\Rightarrow{z}^{'} −{z}\:={x}^{\mathrm{2}} \:+\mathrm{1}\:\left({e}\right) \\ $$$$\left({he}\right)\rightarrow{z}^{'} −{z}\:=\mathrm{0}\:\Rightarrow{z}^{'} \:={z}\:\Rightarrow\frac{{z}^{'} }{{z}}=\mathrm{1}\:\Rightarrow{ln}\mid{z}\mid\:={x}+{c}\:\Rightarrow{z}\:={k}\:{e}^{{x}} \\ $$$${mvc}\:{method}\:\rightarrow{z}^{'} \:={k}^{'} \:{e}^{{x}} \:+{ke}^{{x}} \\ $$$$\left({e}\right)\Rightarrow{k}^{'} \:{e}^{{x}} \:+{ke}^{{x}} −{ke}^{{x}} \:={x}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow{k}^{'} \:=\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}} \:\Rightarrow \\ $$$${k}\left({x}\right)\:=\int\:\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}} \:{dx}\:+{c} \\ $$$$=_{{by}\:{parts}} \:\:\:−\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}} +\int\:\mathrm{2}{x}\:{e}^{−{x}} \:+{c} \\ $$$$=−\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}} \:+\mathrm{2}\left\{\:−{xe}^{−{x}} \:+\int\:{e}^{−{x}} \:{dx}\right\}\:+{c} \\ $$$$=−\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){e}^{−{x}} \:−\mathrm{2}{xe}^{−{x}} −\mathrm{2}{e}^{−{x}} \:+{c} \\ $$$$=−\left({x}^{\mathrm{2}} \:+\mathrm{1}+\mathrm{2}{x}+\mathrm{2}\right){e}^{−{x}} \:+{c}\:=−\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}\right){e}^{−{x}} \:+{c} \\ $$$${z}\left({x}\right)={k}\left({x}\right){e}^{{x}} \:=−\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}\right)+{ce}^{{x}} \\ $$$${y}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:=\mathrm{0}\:\Rightarrow{z}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow−\mathrm{3}+{c}\:=\mathrm{0}\:\Rightarrow{c}=\mathrm{3}\:\Rightarrow{z}\left({x}\right)=\mathrm{3}{e}^{{x}} −{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3} \\ $$$${y}^{\left(\mathrm{2}\right)} \left({x}\right)\:={z}\left({x}\right)\:\Rightarrow{y}^{'} \left({x}\right)\:=\mathrm{3}{e}^{{x}} −\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{3}{x}\:+\lambda\: \\ $$$${y}^{'} \left(\mathrm{0}\right)\:=−\mathrm{1}\:\Rightarrow\mathrm{3}+\lambda\:=−\mathrm{1}\:\Rightarrow\lambda\:=−\mathrm{4}\:\Rightarrow{y}^{'} \left({x}\right)=\mathrm{3}{e}^{{x}} −\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{4} \\ $$$$\Rightarrow{y}\left({x}\right)\:=\mathrm{3}{e}^{{x}} −\frac{\mathrm{1}}{\mathrm{12}}{x}^{\mathrm{4}} −\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} −\mathrm{4}{x}\:+\epsilon \\ $$$${y}\left(\mathrm{0}\right)\:=\mathrm{1}\:\Rightarrow\mathrm{3}\:+\epsilon\:=\mathrm{1}\:\Rightarrow\epsilon\:=−\mathrm{2}\:\Rightarrow \\ $$$${y}\left({x}\right)=\mathrm{3}{e}^{{x}} −\frac{\mathrm{1}}{\mathrm{12}}{x}^{\mathrm{4}} −\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} −\mathrm{4}{x}\:−\mathrm{2} \\ $$
Answered by TANMAY PANACEA. last updated on 06/Apr/20
y=e^(mx) m^3 −m^2 =0 m^2 (m−1) C.F=Ae^(0.x) +Bxe^(0.x) +Ce^x =A+Bx+Ce^x P.I y=((x^2 +1)/(D^2 (D−1)))=(1/(D−1))×(1/D)((x^3 /3)+x)=(((x^4 /(12))+(x^2 /2))/(D−1)) =(−1)(1−D)^(−1) ((x^4 /(12))+(x^2 /2)) =(−1)(1+D+D^2 +D^3 +D^4 +D^5 +D^6 ...)((x^4 /(12))+(x^2 /2)) =(−1)((x^4 /(12))+(x^2 /2)+(x^3 /3)+x+(x^2 /1)+1+2x+0+2) =(−1)((x^4 /(12))+(x^3 /3)+((3x^2 )/2)+3x+3) complete solution y=A+Bx+Ce^x +(−1)((x^4 /(12))+(x^3 /3)+((3x^2 )/2)+3x+3)
$${y}={e}^{{mx}} \\ $$$${m}^{\mathrm{3}} −{m}^{\mathrm{2}} =\mathrm{0} \\ $$$${m}^{\mathrm{2}} \left({m}−\mathrm{1}\right) \\ $$$${C}.{F}={Ae}^{\mathrm{0}.{x}} +{Bxe}^{\mathrm{0}.{x}} +{Ce}^{{x}} ={A}+{Bx}+{Ce}^{{x}} \\ $$$${P}.{I} \\ $$$${y}=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{D}^{\mathrm{2}} \left({D}−\mathrm{1}\right)}=\frac{\mathrm{1}}{{D}−\mathrm{1}}×\frac{\mathrm{1}}{{D}}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+{x}\right)=\frac{\frac{{x}^{\mathrm{4}} }{\mathrm{12}}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}{{D}−\mathrm{1}} \\ $$$$=\left(−\mathrm{1}\right)\left(\mathrm{1}−{D}\right)^{−\mathrm{1}} \left(\frac{{x}^{\mathrm{4}} }{\mathrm{12}}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$=\left(−\mathrm{1}\right)\left(\mathrm{1}+{D}+{D}^{\mathrm{2}} +{D}^{\mathrm{3}} +{D}^{\mathrm{4}} +{D}^{\mathrm{5}} +{D}^{\mathrm{6}} …\right)\left(\frac{{x}^{\mathrm{4}} }{\mathrm{12}}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$=\left(−\mathrm{1}\right)\left(\frac{{x}^{\mathrm{4}} }{\mathrm{12}}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{1}}+\mathrm{1}+\mathrm{2}{x}+\mathrm{0}+\mathrm{2}\right) \\ $$$$=\left(−\mathrm{1}\right)\left(\frac{{x}^{\mathrm{4}} }{\mathrm{12}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{3}{x}+\mathrm{3}\right) \\ $$$${complete}\:{solution} \\ $$$${y}={A}+{Bx}+{Ce}^{{x}} +\left(−\mathrm{1}\right)\left(\frac{{x}^{\mathrm{4}} }{\mathrm{12}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{3}{x}+\mathrm{3}\right) \\ $$$$ \\ $$
Commented by john santu last updated on 06/Apr/20
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *