Question Number 183210 by Mastermind last updated on 23/Dec/22

$$\frac{\mathrm{d}^{\mathrm{3}} \mathrm{y}}{\mathrm{dx}^{\mathrm{3}} }+\mathrm{4}\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }+\frac{\mathrm{dy}}{\mathrm{dx}}−\mathrm{6y}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$
Answered by aleks041103 last updated on 23/Dec/22
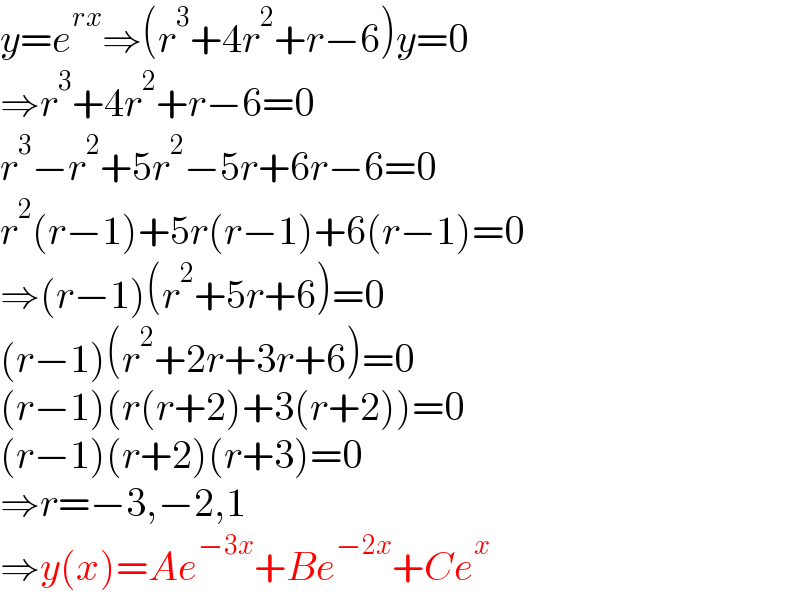
$${y}={e}^{{rx}} \Rightarrow\left({r}^{\mathrm{3}} +\mathrm{4}{r}^{\mathrm{2}} +{r}−\mathrm{6}\right){y}=\mathrm{0} \\ $$$$\Rightarrow{r}^{\mathrm{3}} +\mathrm{4}{r}^{\mathrm{2}} +{r}−\mathrm{6}=\mathrm{0} \\ $$$${r}^{\mathrm{3}} −{r}^{\mathrm{2}} +\mathrm{5}{r}^{\mathrm{2}} −\mathrm{5}{r}+\mathrm{6}{r}−\mathrm{6}=\mathrm{0} \\ $$$${r}^{\mathrm{2}} \left({r}−\mathrm{1}\right)+\mathrm{5}{r}\left({r}−\mathrm{1}\right)+\mathrm{6}\left({r}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({r}−\mathrm{1}\right)\left({r}^{\mathrm{2}} +\mathrm{5}{r}+\mathrm{6}\right)=\mathrm{0} \\ $$$$\left({r}−\mathrm{1}\right)\left({r}^{\mathrm{2}} +\mathrm{2}{r}+\mathrm{3}{r}+\mathrm{6}\right)=\mathrm{0} \\ $$$$\left({r}−\mathrm{1}\right)\left({r}\left({r}+\mathrm{2}\right)+\mathrm{3}\left({r}+\mathrm{2}\right)\right)=\mathrm{0} \\ $$$$\left({r}−\mathrm{1}\right)\left({r}+\mathrm{2}\right)\left({r}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow{r}=−\mathrm{3},−\mathrm{2},\mathrm{1} \\ $$$$\Rightarrow{y}\left({x}\right)={Ae}^{−\mathrm{3}{x}} +{Be}^{−\mathrm{2}{x}} +{Ce}^{{x}} \\ $$
