Question Number 146442 by qaz last updated on 13/Jul/21

$$\frac{\mathrm{d}}{\mathrm{dn}}\mid_{\mathrm{n}=\mathrm{1}} \mathrm{H}_{\mathrm{n}} =? \\ $$
Answered by mnjuly1970 last updated on 13/Jul/21

$$=\:\frac{{d}}{{dn}}\left(\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−{x}^{\:{n}} }{\mathrm{1}−{x}}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{−{x}^{\:{n}} {ln}\left({x}\:\right)}{\mathrm{1}−{x}}{dx} \\ $$$$\:\:\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{−{xln}\left({x}\right)}{\mathrm{1}−{x}}\:{dx}=−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx} \\ $$$$=\:{li}_{\mathrm{2}} \left(\:\mathrm{1}\right)\:+\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right){dx} \\ $$$$\:=\:\frac{\pi^{\:\mathrm{2}} }{\mathrm{6}}\:+\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left({x}\right){dx}=−\mathrm{1}+\frac{\pi^{\:\mathrm{2}} }{\mathrm{6}}\:…. \\ $$
Answered by mnjuly1970 last updated on 13/Jul/21
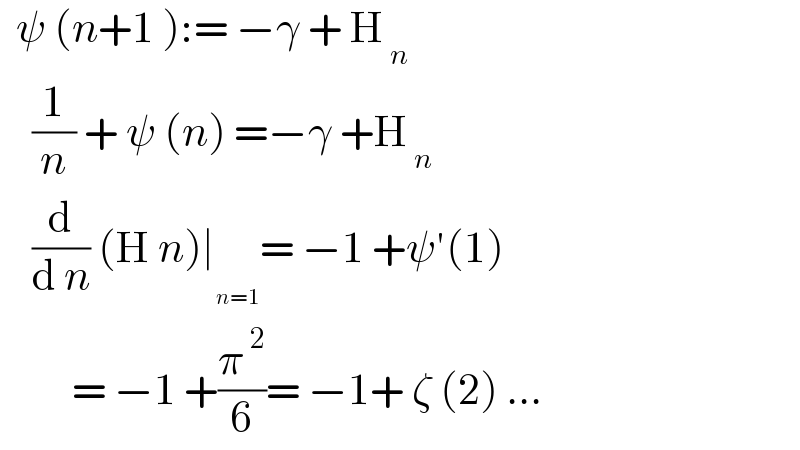
$$\:\:\psi\:\left({n}+\mathrm{1}\:\right):=\:−\gamma\:+\:\mathrm{H}_{\:{n}} \\ $$$$\:\:\:\:\frac{\mathrm{1}}{{n}}\:+\:\psi\:\left({n}\right)\:=−\gamma\:+\mathrm{H}_{\:{n}} \\ $$$$\:\:\:\:\frac{\mathrm{d}}{\mathrm{d}\:{n}}\:\left(\mathrm{H}\:{n}\right)\underset{} {\mid}=\:−\mathrm{1}\:+\psi'\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\:−\mathrm{1}\:+\frac{\pi^{\:\mathrm{2}} }{\mathrm{6}}=\:−\mathrm{1}+\:\zeta\:\left(\mathrm{2}\right)\:… \\ $$
Commented by qaz last updated on 13/Jul/21

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{is}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{use}\:\mathrm{differential}\:\mathrm{chain}\:\mathrm{rule}, \\ $$$$\mathrm{same}\:\mathrm{like}\:\frac{\partial}{\partial\mathrm{x}}\int_{\mathrm{h}\left(\mathrm{x}\right)} ^{\mathrm{g}\left(\mathrm{x}\right)} \mathrm{f}\left(\mathrm{x},\mathrm{t}\right)\mathrm{dt}=\int_{\mathrm{h}\left(\mathrm{x}\right)} ^{\mathrm{g}\left(\mathrm{x}\right)} \frac{\partial}{\partial\mathrm{x}}\mathrm{f}\left(\mathrm{x},\mathrm{t}\right)\mathrm{dt}+\mathrm{g}\left(\mathrm{x}\right)'\mathrm{f}\left(\mathrm{x},\mathrm{g}\left(\mathrm{x}\right)\right)−\mathrm{h}\left(\mathrm{x}\right)'\mathrm{f}\left(\mathrm{x},\mathrm{h}\left(\mathrm{x}\right)\right) \\ $$$$,\mathrm{to}\:\mathrm{differential}\:\mathrm{to}\:\mathrm{a}\:\mathrm{seiris}\:\mathrm{summation}….. \\ $$
Commented by mnjuly1970 last updated on 13/Jul/21

$${thank}\:{you}\:{sir}\:{qaz} \\ $$
