Question Number 117759 by Dwaipayan Shikari last updated on 13/Oct/20
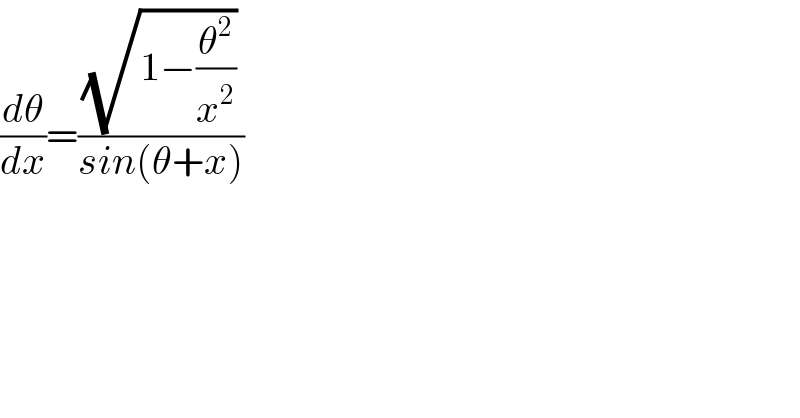
$$\frac{{d}\theta}{{dx}}=\frac{\sqrt{\mathrm{1}−\frac{\theta^{\mathrm{2}} }{{x}^{\mathrm{2}} }}}{{sin}\left(\theta+{x}\right)} \\ $$
Commented by TANMAY PANACEA last updated on 13/Oct/20
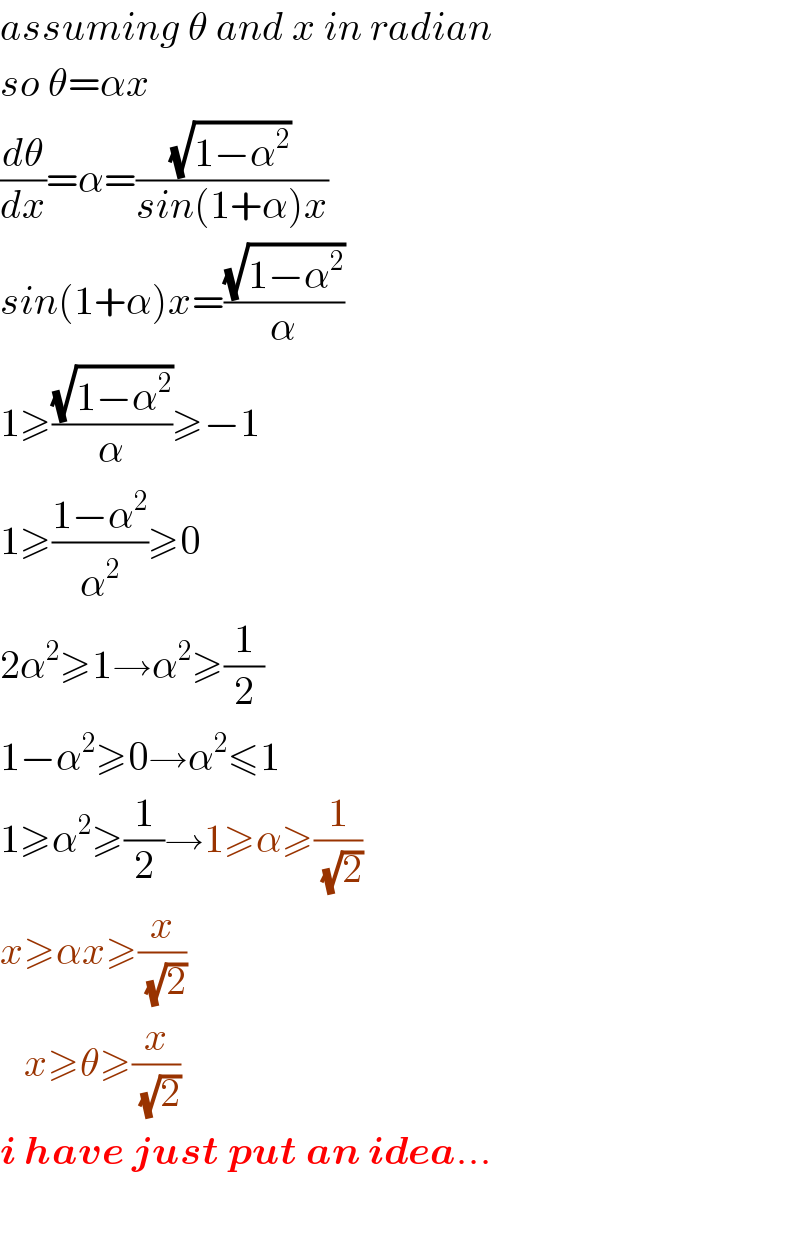
$${assuming}\:\theta\:{and}\:{x}\:{in}\:{radian} \\ $$$${so}\:\theta=\alpha{x} \\ $$$$\frac{{d}\theta}{{dx}}=\alpha=\frac{\sqrt{\mathrm{1}−\alpha^{\mathrm{2}} }}{{sin}\left(\mathrm{1}+\alpha\right){x}} \\ $$$${sin}\left(\mathrm{1}+\alpha\right){x}=\frac{\sqrt{\mathrm{1}−\alpha^{\mathrm{2}} }}{\alpha} \\ $$$$\mathrm{1}\geqslant\frac{\sqrt{\mathrm{1}−\alpha^{\mathrm{2}} }}{\alpha}\geqslant−\mathrm{1} \\ $$$$\mathrm{1}\geqslant\frac{\mathrm{1}−\alpha^{\mathrm{2}} }{\alpha^{\mathrm{2}} }\geqslant\mathrm{0} \\ $$$$\mathrm{2}\alpha^{\mathrm{2}} \geqslant\mathrm{1}\rightarrow\alpha^{\mathrm{2}} \geqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{1}−\alpha^{\mathrm{2}} \geqslant\mathrm{0}\rightarrow\alpha^{\mathrm{2}} \leqslant\mathrm{1} \\ $$$$\mathrm{1}\geqslant\alpha^{\mathrm{2}} \geqslant\frac{\mathrm{1}}{\mathrm{2}}\rightarrow\mathrm{1}\geqslant\alpha\geqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${x}\geqslant\alpha{x}\geqslant\frac{{x}}{\:\sqrt{\mathrm{2}}} \\ $$$$\:\:\:{x}\geqslant\theta\geqslant\frac{{x}}{\:\sqrt{\mathrm{2}}} \\ $$$$\boldsymbol{{i}}\:\boldsymbol{{have}}\:\boldsymbol{{just}}\:\boldsymbol{{put}}\:\boldsymbol{{an}}\:\boldsymbol{{idea}}… \\ $$$$ \\ $$
