Question Number 170255 by mathlove last updated on 19/May/22
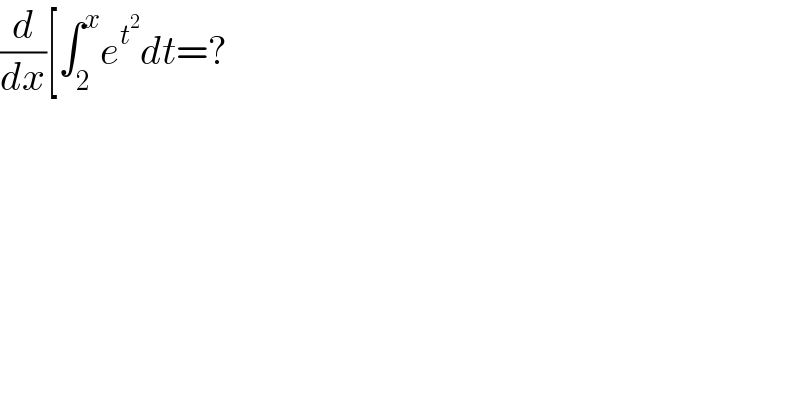
$$\frac{{d}}{{dx}}\left[\int_{\mathrm{2}} ^{{x}} {e}^{{t}^{\mathrm{2}} } {dt}=?\right. \\ $$
Answered by floor(10²Eta[1]) last updated on 19/May/22
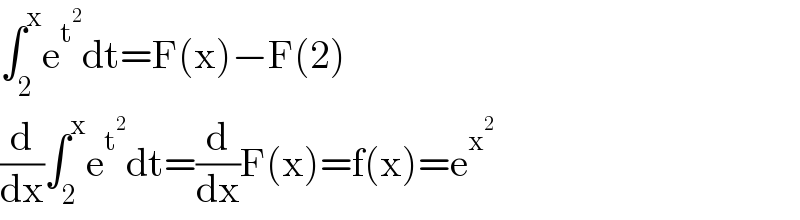
$$\int_{\mathrm{2}} ^{\mathrm{x}} \mathrm{e}^{\mathrm{t}^{\mathrm{2}} } \mathrm{dt}=\mathrm{F}\left(\mathrm{x}\right)−\mathrm{F}\left(\mathrm{2}\right) \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\int_{\mathrm{2}} ^{\mathrm{x}} \mathrm{e}^{\mathrm{t}^{\mathrm{2}} } \mathrm{dt}=\frac{\mathrm{d}}{\mathrm{dx}}\mathrm{F}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } \\ $$
