Question Number 32980 by Nayon.Sm last updated on 08/Apr/18
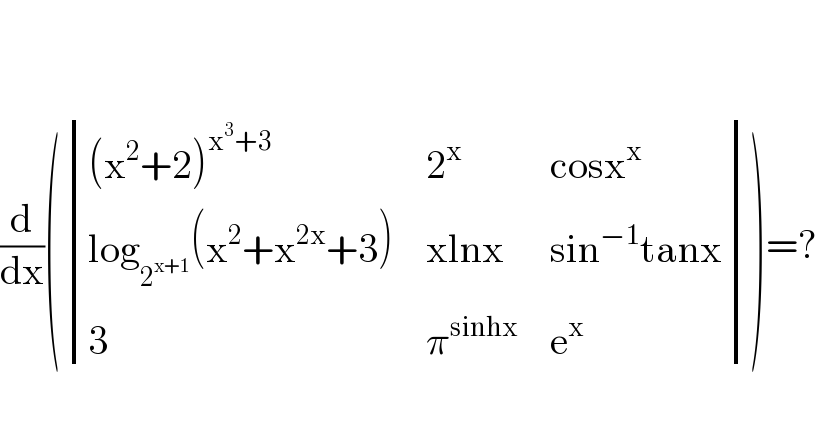
$$ \\ $$$$ \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\begin{vmatrix}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{x}^{\mathrm{3}} +\mathrm{3}} }&{\mathrm{2}^{\mathrm{x}} }&{\mathrm{cosx}^{\mathrm{x}} }\\{\mathrm{log}_{\mathrm{2}^{\mathrm{x}+\mathrm{1}} } \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2x}} +\overset{} {\mathrm{3}}\right)}&{\mathrm{xlnx}}&{\mathrm{sin}^{−\mathrm{1}} \mathrm{tanx}}\\{\mathrm{3}}&{\pi^{\mathrm{sinhx}} }&{\mathrm{e}^{\mathrm{x}} }\end{vmatrix}\right)=? \\ $$$$ \\ $$
Answered by MJS last updated on 08/Apr/18
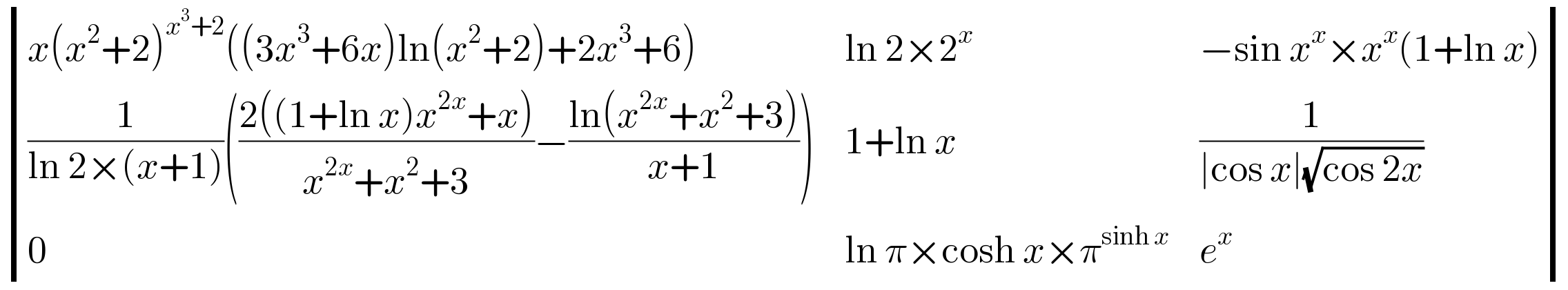
$$\begin{vmatrix}{{x}\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{{x}^{\mathrm{3}} +\mathrm{2}} \left(\left(\mathrm{3}{x}^{\mathrm{3}} +\mathrm{6}{x}\right)\mathrm{ln}\left({x}^{\mathrm{2}} +\mathrm{2}\right)+\mathrm{2}{x}^{\mathrm{3}} +\mathrm{6}\right)}&{\mathrm{ln}\:\mathrm{2}×\mathrm{2}^{{x}} }&{−\mathrm{sin}\:{x}^{{x}} ×{x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right)}\\{\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{2}×\left({x}+\mathrm{1}\right)}\left(\frac{\mathrm{2}\left(\left(\mathrm{1}+\mathrm{ln}\:{x}\right){x}^{\mathrm{2}{x}} +{x}\right)}{{x}^{\mathrm{2}{x}} +{x}^{\mathrm{2}} +\mathrm{3}}−\frac{\mathrm{ln}\left({x}^{\mathrm{2}{x}} +{x}^{\mathrm{2}} +\mathrm{3}\right)}{{x}+\mathrm{1}}\right)}&{\mathrm{1}+\mathrm{ln}\:{x}}&{\frac{\mathrm{1}}{\mid\mathrm{cos}\:{x}\mid\sqrt{\mathrm{cos}\:\mathrm{2}{x}}}}\\{\mathrm{0}}&{\mathrm{ln}\:\pi×\mathrm{cosh}\:{x}×\pi^{\mathrm{sinh}\:{x}} }&{{e}^{{x}} }\end{vmatrix} \\ $$
Commented by Nayon.Sm last updated on 15/Apr/18

$$\mathrm{wron}\overset{} {\mathrm{g}} \\ $$
