Menu Close

d-dx-sin-1-2x-1-x-2-atx-1-

Tinku Tara 0 Comments
Pin




Question Number 117470 by TANMAY PANACEA last updated on 11/Oct/20
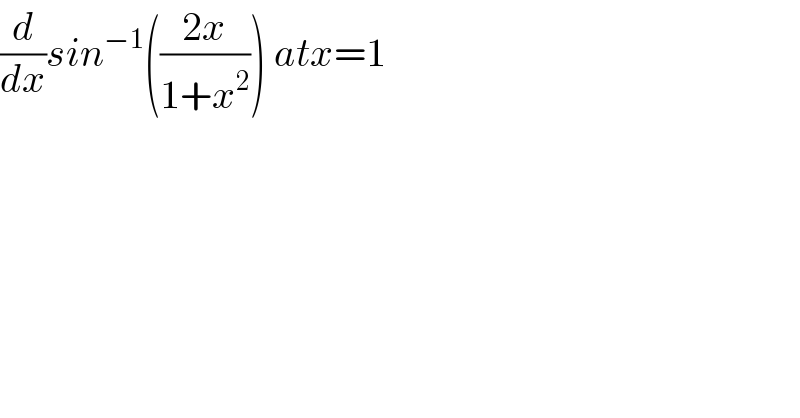
(d/dx)sin^(−1) (((2x)/(1+x^2 ))) atx=1
$$\frac{{d}}{{dx}}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:{atx}=\mathrm{1} \\ $$
Commented by TANMAY PANACEA last updated on 12/Oct/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Commented by Dwaipayan Shikari last updated on 11/Oct/20
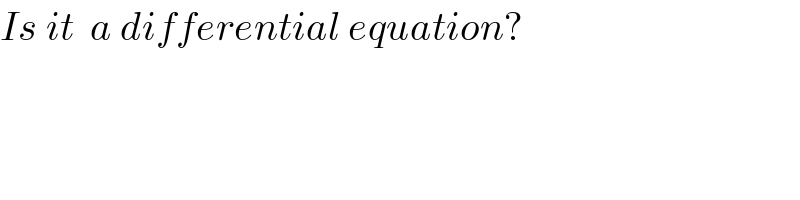
Is it a differential equation?
$${Is}\:{it}\:\:{a}\:{differential}\:{equation}? \\ $$
Commented by TANMAY PANACEA last updated on 11/Oct/20
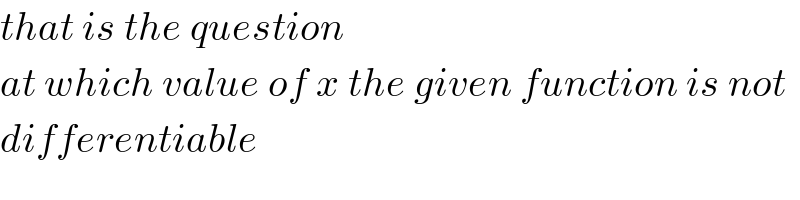
that is the question at which value of x the given function is not differentiable
$${that}\:{is}\:{the}\:{question} \\ $$$${at}\:{which}\:{value}\:{of}\:{x}\:{the}\:{given}\:{function}\:{is}\:{not} \\ $$$${differentiable} \\ $$
Commented by MJS_new last updated on 12/Oct/20
(d/dx)[arcsin ((2x)/(1+x^2 ))]=(1/( (√(1−(((2x)/(1+x^2 )))^2 ))))×((2(1−x^2 ))/((1+x^2 )^2 ))= =−(2/(1+x^2 ))sign (x^2 −1) but sign 0 is not defined ⇒ sin^(−1) ((2x)/(1+x^2 )) is not differentiable at x=±1
$$\frac{{d}}{{dx}}\left[\mathrm{arcsin}\:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right]=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left(\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }}×\frac{\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }= \\ $$$$=−\frac{\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} }\mathrm{sign}\:\left({x}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\mathrm{but}\:\mathrm{sign}\:\mathrm{0}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined} \\ $$$$\Rightarrow\:\mathrm{sin}^{−\mathrm{1}} \:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{not}\:\mathrm{differentiable}\:\mathrm{at}\:{x}=\pm\mathrm{1} \\ $$
Commented by TANMAY PANACEA last updated on 12/Oct/20
from graph it is clear that we can not draw tangent at x=1 so it is not differentiable at x=1
$$\boldsymbol{{from}}\:\boldsymbol{{graph}}\:\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{clear}}\:\boldsymbol{{that}}\:\boldsymbol{{we}}\:\boldsymbol{{can}}\:\boldsymbol{{not}}\:\boldsymbol{{draw}} \\ $$$$\boldsymbol{{tangent}}\:\boldsymbol{{at}}\:\boldsymbol{{x}}=\mathrm{1}\:\boldsymbol{{so}}\:\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{not}}\:\boldsymbol{{differentiable}} \\ $$$$\boldsymbol{{at}}\:\boldsymbol{{x}}=\mathrm{1} \\ $$
Answered by Lordose last updated on 11/Oct/20
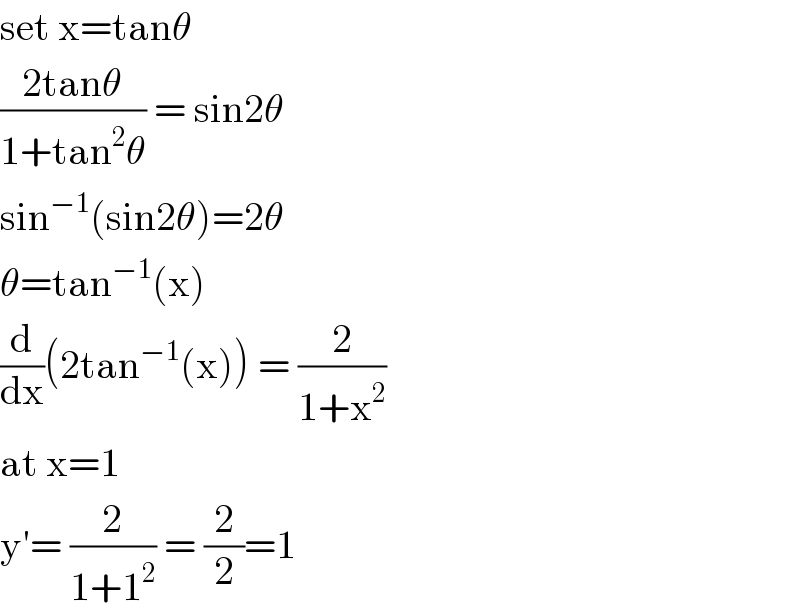
set x=tanθ ((2tanθ)/(1+tan^2 θ)) = sin2θ sin^(−1) (sin2θ)=2θ θ=tan^(−1) (x) (d/dx)(2tan^(−1) (x)) = (2/(1+x^2 )) at x=1 y′= (2/(1+1^2 )) = (2/2)=1
$$\mathrm{set}\:\mathrm{x}=\mathrm{tan}\theta \\ $$$$\frac{\mathrm{2tan}\theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}\:=\:\mathrm{sin2}\theta \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin2}\theta\right)=\mathrm{2}\theta \\ $$$$\theta=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right) \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{2tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)\:=\:\frac{\mathrm{2}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{at}\:\mathrm{x}=\mathrm{1} \\ $$$$\mathrm{y}'=\:\frac{\mathrm{2}}{\mathrm{1}+\mathrm{1}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}}{\mathrm{2}}=\mathrm{1} \\ $$
Commented by TANMAY PANACEA last updated on 12/Oct/20
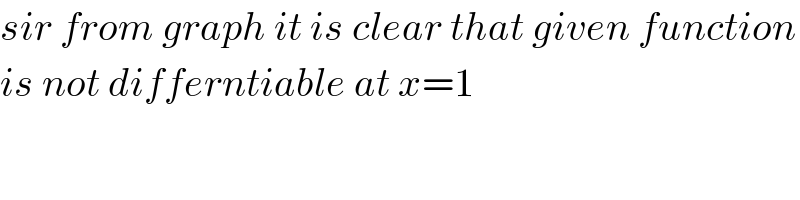
sir from graph it is clear that given function is not differntiable at x=1
$${sir}\:{from}\:{graph}\:{it}\:{is}\:{clear}\:{that}\:{given}\:{function} \\ $$$${is}\:{not}\:{differntiable}\:{at}\:{x}=\mathrm{1} \\ $$
Answered by Olaf last updated on 11/Oct/20
((darcsinu)/du) = (du/dx).(1/( (√(1−u^2 )))) u = ((2x)/(1+x^2 )) (du/dx) = 2((1+x^2 −x(2x))/((1+x^2 )^2 )) = ((2(1−x^2 ))/((1+x^2 ))) ((darcsinu)/du) = ((2(1−x^2 ))/((1+x^2 )^2 (√(1−(((2x)/(1+x^2 )))^2 )))) ((darcsinu)/du) = ((2(1−x^2 ))/((1+x^2 )(√((1+x^2 )^2 −4x^2 )))) ((darcsinu)/du) = ((2(1−x^2 ))/((1+x^2 )(√((x^4 −2x^2 +1)))) ((darcsinu)/du) = ((2(1−x^2 ))/((1+x^2 )(√((1−x^2 ))))) = (2/(1+x^2 )) ⇒ ((darcsinu)/du) = 1 at x = 1
$$\frac{{d}\mathrm{arcsin}{u}}{{du}}\:=\:\frac{{du}}{{dx}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }} \\ $$$${u}\:=\:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\frac{{du}}{{dx}}\:=\:\mathrm{2}\frac{\mathrm{1}+{x}^{\mathrm{2}} −{x}\left(\mathrm{2}{x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\:\frac{\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$$\frac{{d}\mathrm{arcsin}{u}}{{du}}\:=\:\frac{\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} \sqrt{\mathrm{1}−\left(\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }} \\ $$$$\frac{{d}\mathrm{arcsin}{u}}{{du}}\:=\:\frac{\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} }} \\ $$$$\frac{{d}\mathrm{arcsin}{u}}{{du}}\:=\:\frac{\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\left({x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right.}} \\ $$$$\frac{{d}\mathrm{arcsin}{u}}{{du}}\:=\:\frac{\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}}\:=\:\frac{\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{{d}\mathrm{arcsin}{u}}{{du}}\:=\:\mathrm{1}\:\mathrm{at}\:{x}\:=\:\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 11/Oct/20
let f(x)=arcsin(((2x)/(1+x^2 ))) f^′ (1)? f^′ (x)=(((((2x)/(1+x^2 )))^′ )/( (√(1−(((2x)/(1+x^2 )))^2 )))) =((2(1+x^2 )−2x(2x))/((1+x^2 )^2 ))×(1/( (√((1+x^2 )^2 −4x^2 ))))×(1+x^2 ) =((2−2x^2 )/((1+x^2 )(√(x^4 +2x^2 +1−4x^2 )))) =((2(1−x^2 ))/((1+x^2 )(√((x^2 −1)^2 )))) =((2(1−x^2 ))/((1+x^2 )∣1−x^2 ∣)) so its seems that f is not derivable at x_0 =1 but lim_(x→1^+ ) f^′ (x) =lim_(x→1^+ ) ((−2)/(1+x^2 ))=−1 and lim_(x→1^− ) f^′ (x)=lim_(x→1^− ) (2/(1+x^2 )) =1
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{arcsin}\left(\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\:\:\:\mathrm{f}^{'} \left(\mathrm{1}\right)? \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)=\frac{\left(\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)^{'} }{\:\sqrt{\mathrm{1}−\left(\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }}\:=\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)−\mathrm{2x}\left(\mathrm{2x}\right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }×\frac{\mathrm{1}}{\:\sqrt{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4x}^{\mathrm{2}} }}×\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right) \\ $$$$=\frac{\mathrm{2}−\mathrm{2x}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{2}} +\mathrm{1}−\mathrm{4x}^{\mathrm{2}} }}\:=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\sqrt{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mid\mathrm{1}−\mathrm{x}^{\mathrm{2}} \mid}\:\mathrm{so}\:\mathrm{its}\:\mathrm{seems}\:\mathrm{that}\:\mathrm{f}\:\mathrm{is}\:\mathrm{not}\:\mathrm{derivable}\:\mathrm{at}\:\mathrm{x}_{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{but}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \:\:\mathrm{f}^{'} \left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \:\:\frac{−\mathrm{2}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=−\mathrm{1}\:\mathrm{and} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{−} } \:\:\mathrm{f}^{'} \left(\mathrm{x}\right)=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{−} } \:\:\frac{\mathrm{2}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\mathrm{1} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *