Menu Close

d-dx-x-

Tinku Tara 0 Comments
Pin




Question Number 101104 by student work last updated on 30/Jun/20
(d/dx)(x!)=?
$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}!\right)=? \\ $$
Answered by smridha last updated on 30/Jun/20
x!=πšͺ(x+1)=xΞ“x =lim_(nβ†’βˆž) ((n!)/((x+1)(x+2)......(x+n)))n^x [Euler definition] take ln both sides we get ln[πšͺ(x+1)]=lim_(nβ†’βˆž) [ln(n!)+xln(n)βˆ’ln(x+1)βˆ’ln(x+2)βˆ’.....βˆ’ln(x+n)] now diff: both sides wrt x (([πšͺ(x+1)]^β€² )/(πšͺ(x+1)))β‰‘πšΏ(x+1)[Digamma f^n ] =lim_(nβ†’βˆž) [ln(n)βˆ’(1/((x+1)))βˆ’(1/((x+2)))βˆ’...(1/((x+n)))] so 𝚿(x+1)=lim_(nβ†’βˆž) [(ln(n)βˆ’H_n )βˆ’Ξ£_(m=1) ^n ((1/((x+m)))βˆ’(1/m))] =βˆ’π›„+Ξ£_(m=1) ^∞ (x/(m(m+x))) so,[πšͺ(x+1)]^β€² =πšͺ(x+1).𝚿(x+1). where... 𝛄(Eulerβˆ’Mascheroni constant) defind by 𝛄=lim_(nβ†’βˆž) (H_n βˆ’ln(n)) H_n (harmonic number)=Ξ£_(m=1) ^n (1/m).
$$\boldsymbol{{x}}!=\boldsymbol{\Gamma}\left(\boldsymbol{{x}}+\mathrm{1}\right)=\boldsymbol{{x}}\Gamma\boldsymbol{{x}} \\ $$$$=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\boldsymbol{{n}}!}{\left(\boldsymbol{{x}}+\mathrm{1}\right)\left(\boldsymbol{{x}}+\mathrm{2}\right)……\left(\boldsymbol{{x}}+\boldsymbol{{n}}\right)}\boldsymbol{{n}}^{\boldsymbol{{x}}} \left[\boldsymbol{{E}}{u}\boldsymbol{{ler}}\:\boldsymbol{{definition}}\right] \\ $$$$\boldsymbol{{take}}\:\boldsymbol{{ln}}\:\boldsymbol{{both}}\:\boldsymbol{{sides}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\boldsymbol{{ln}}\left[\boldsymbol{\Gamma}\left(\boldsymbol{{x}}+\mathrm{1}\right)\right]=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\left[{l}\boldsymbol{{n}}\left(\boldsymbol{{n}}!\right)+\boldsymbol{{xln}}\left(\boldsymbol{{n}}\right)βˆ’\boldsymbol{{ln}}\left(\boldsymbol{{x}}+\mathrm{1}\right)βˆ’\boldsymbol{{ln}}\left(\boldsymbol{{x}}+\mathrm{2}\right)βˆ’…..βˆ’\boldsymbol{{ln}}\left(\boldsymbol{{x}}+\boldsymbol{{n}}\right)\right] \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{diff}}:\:\boldsymbol{{both}}\:\boldsymbol{{sides}}\:\boldsymbol{{wrt}}\:\boldsymbol{{x}} \\ $$$$\frac{\left[\boldsymbol{\Gamma}\left(\boldsymbol{{x}}+\mathrm{1}\right)\right]^{'} }{\boldsymbol{\Gamma}\left(\boldsymbol{{x}}+\mathrm{1}\right)}\equiv\boldsymbol{\Psi}\left(\boldsymbol{{x}}+\mathrm{1}\right)\left[\boldsymbol{{Digamma}}\:\boldsymbol{{f}}^{\boldsymbol{{n}}} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\left[\boldsymbol{{ln}}\left(\boldsymbol{{n}}\right)βˆ’\frac{\mathrm{1}}{\left(\boldsymbol{{x}}+\mathrm{1}\right)}βˆ’\frac{\mathrm{1}}{\left(\boldsymbol{{x}}+\mathrm{2}\right)}βˆ’…\frac{\mathrm{1}}{\left(\boldsymbol{{x}}+\boldsymbol{{n}}\right)}\right] \\ $$$$\:\:\:\boldsymbol{{so}}\:\boldsymbol{\Psi}\left(\boldsymbol{{x}}+\mathrm{1}\right)=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\left[\left(\boldsymbol{{ln}}\left(\boldsymbol{{n}}\right)βˆ’\boldsymbol{{H}}_{{n}} \right)βˆ’\underset{\boldsymbol{{m}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\left(\frac{\mathrm{1}}{\left(\boldsymbol{{x}}+\boldsymbol{{m}}\right)}βˆ’\frac{\mathrm{1}}{\boldsymbol{{m}}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=βˆ’\boldsymbol{\gamma}+\underset{\boldsymbol{{m}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\boldsymbol{{x}}}{\boldsymbol{{m}}\left(\boldsymbol{{m}}+\boldsymbol{{x}}\right)} \\ $$$$\boldsymbol{{so}},\left[\boldsymbol{\Gamma}\left(\boldsymbol{{x}}+\mathrm{1}\right)\right]^{'} =\boldsymbol{\Gamma}\left(\boldsymbol{{x}}+\mathrm{1}\right).\boldsymbol{\Psi}\left(\boldsymbol{{x}}+\mathrm{1}\right). \\ $$$$\boldsymbol{{where}}… \\ $$$$\boldsymbol{\gamma}\left(\boldsymbol{{E}}{uler}βˆ’\boldsymbol{{Mascheroni}}\:\boldsymbol{{constant}}\right) \\ $$$$\boldsymbol{{defind}}\:\boldsymbol{{by}} \\ $$$$\boldsymbol{\gamma}=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\left(\boldsymbol{{H}}_{\boldsymbol{{n}}} βˆ’\boldsymbol{{ln}}\left(\boldsymbol{{n}}\right)\right) \\ $$$$\boldsymbol{{H}}_{\boldsymbol{{n}}} \left(\boldsymbol{{harmonic}}\:\boldsymbol{{number}}\right)=\underset{\boldsymbol{{m}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\frac{\mathrm{1}}{\boldsymbol{{m}}}. \\ $$
Commented by MJS last updated on 30/Jun/20
Ξ“(x+1)=∫_0 ^∞ t^x e^(βˆ’t) dt (d/dx)[Ξ“(x+1)]=∫_0 ^∞ t^x e^(βˆ’t) ln t dt which is not easier or harder to calculate than your answer
$$\Gamma\left({x}+\mathrm{1}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}{t}^{{x}} \mathrm{e}^{βˆ’{t}} {dt} \\ $$$$\frac{{d}}{{dx}}\left[\Gamma\left({x}+\mathrm{1}\right)\right]=\underset{\mathrm{0}} {\overset{\infty} {\int}}{t}^{{x}} \mathrm{e}^{βˆ’{t}} \mathrm{ln}\:{t}\:{dt} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{not}\:\mathrm{easier}\:\mathrm{or}\:\mathrm{harder}\:\mathrm{to}\:\mathrm{calculate} \\ $$$$\mathrm{than}\:\mathrm{your}\:\mathrm{answer} \\ $$
Commented by smridha last updated on 30/Jun/20
my way is the standard way and the result is also standard.. your method is just a application of my method.many of the conclutions can be derived by the way I approched. I have an another interesting way infinite product of gamma f^n Weierstrass form (1/(πšͺ(x)))≑xe^(𝛄x) Ξ _(n=1) ^∞ (1+(x/n))e^(βˆ’(x/n)) the same result can be evaluated from this. I always show my favourite method among the methods I know!!!
$$\boldsymbol{{my}}\:\boldsymbol{{way}}\:\boldsymbol{{is}}\:\boldsymbol{{the}}\:\boldsymbol{{standard}}\:\boldsymbol{{way}}\: \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{the}}\:\boldsymbol{{result}}\:\boldsymbol{{is}}\:\boldsymbol{{also}}\:\boldsymbol{{standard}}.. \\ $$$$\boldsymbol{{your}}\:\boldsymbol{{method}}\:\boldsymbol{{is}}\:\boldsymbol{{just}}\:\boldsymbol{{a}}\:\boldsymbol{{application}} \\ $$$$\boldsymbol{{of}}\:\boldsymbol{{my}}\:\boldsymbol{{method}}.\boldsymbol{{many}}\:\boldsymbol{{of}}\:\boldsymbol{{the}}\: \\ $$$$\boldsymbol{{conclutions}}\:\boldsymbol{{can}}\:\boldsymbol{{be}}\:\boldsymbol{{derived}}\:\boldsymbol{{by}} \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{way}}\:\boldsymbol{{I}}\:\boldsymbol{{approched}}. \\ $$$$\boldsymbol{{I}}\:\:\boldsymbol{{have}}\:\boldsymbol{{an}}\:\boldsymbol{{another}}\:\boldsymbol{{interesting}}\:\boldsymbol{{way}} \\ $$$$\boldsymbol{{infinite}}\:\boldsymbol{{product}}\:\boldsymbol{{of}}\:\boldsymbol{{gamma}}\:\boldsymbol{{f}}^{\boldsymbol{{n}}} \\ $$$$\boldsymbol{{Weierstrass}}\:\boldsymbol{{form}}\: \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\boldsymbol{\Gamma}\left({x}\right)}\equiv\boldsymbol{{xe}}^{\boldsymbol{\gamma{x}}} \underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{\boldsymbol{{x}}}{\boldsymbol{{n}}}\right)\boldsymbol{{e}}^{βˆ’\frac{\boldsymbol{{x}}}{\boldsymbol{{n}}}} \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{same}}\:\boldsymbol{{result}}\:\boldsymbol{{can}}\:\boldsymbol{{be}}\:\boldsymbol{{evaluated}} \\ $$$$\boldsymbol{{from}}\:\boldsymbol{{this}}. \\ $$$$\boldsymbol{{I}}\:\boldsymbol{{always}}\:\boldsymbol{{show}}\:\boldsymbol{{my}}\:\boldsymbol{{favourite}}\:\boldsymbol{{method}} \\ $$$$\boldsymbol{{among}}\:\boldsymbol{{the}}\:\boldsymbol{{methods}}\:\boldsymbol{{I}}\:\boldsymbol{{know}}!!! \\ $$
Commented by Shazneen last updated on 01/Jul/20
simple to understand
Commented by Tawa11 last updated on 06/Nov/21
Good
$$\mathrm{Good} \\ $$
Answered by Β MΒ±th+et+s last updated on 30/Jun/20
∡x!=(√(2Ο€x))((x/e))^x β‡’(d/dx)(x!)=(√(2Ο€x)).e^(x(ln(x)βˆ’)) .(x.(1/x)+ln(x)βˆ’1)+e^(x(ln(x)βˆ’1)) ((2Ο€)/( (√(2Ο€x)))) =e^(x(ln(x)βˆ’1)) ((√(2Ο€x)) ln(x)+((2Ο€)/( (√(2Ο€x))))) ∴(d/dx)(x!)=((2Ο€.e^(x(ln(x)βˆ’1)) )/( (√(2Ο€x))))(xln(x)+1)
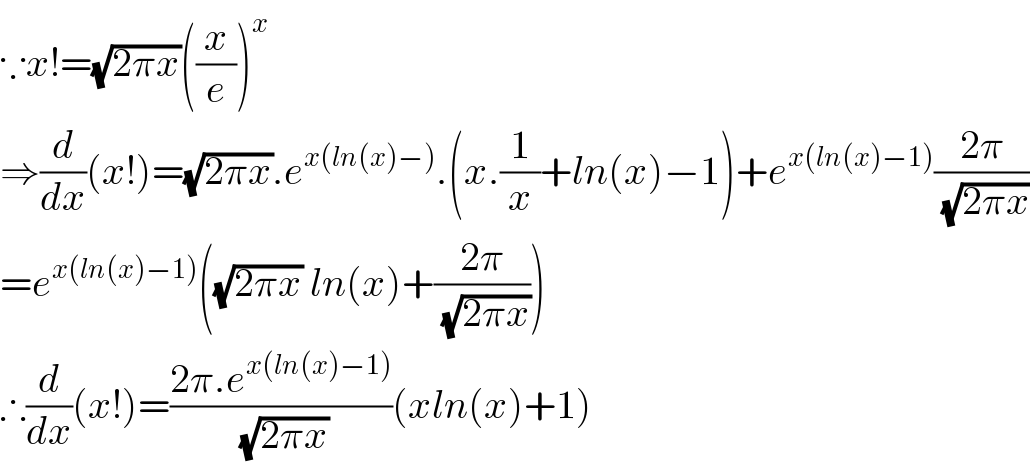
$$\because{x}!=\sqrt{\mathrm{2}\pi{x}}\left(\frac{{x}}{{e}}\right)^{{x}} \\ $$$$\Rightarrow\frac{{d}}{{dx}}\left({x}!\right)=\sqrt{\mathrm{2}\pi{x}}.{e}^{{x}\left({ln}\left({x}\right)βˆ’\right)} .\left({x}.\frac{\mathrm{1}}{{x}}+{ln}\left({x}\right)βˆ’\mathrm{1}\right)+{e}^{{x}\left({ln}\left({x}\right)βˆ’\mathrm{1}\right)} \frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{2}\pi{x}}} \\ $$$$={e}^{{x}\left({ln}\left({x}\right)βˆ’\mathrm{1}\right)} \left(\sqrt{\mathrm{2}\pi{x}}\:{ln}\left({x}\right)+\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{2}\pi{x}}}\right) \\ $$$$\therefore\frac{{d}}{{dx}}\left({x}!\right)=\frac{\mathrm{2}\pi.{e}^{{x}\left({ln}\left({x}\right)βˆ’\mathrm{1}\right)} }{\:\sqrt{\mathrm{2}\pi{x}}}\left({xln}\left({x}\right)+\mathrm{1}\right) \\ $$
Commented by smridha last updated on 30/Jun/20
stirlingβ€²s formula very good!! i know also but it is approximate result: because πšͺ(x+1)β‰ˆ(√(2𝛑x)).x^x .e^(βˆ’x)
$$\boldsymbol{{stirling}}'{s}\:\boldsymbol{{formula}}\:\boldsymbol{{very}}\:\boldsymbol{{good}}!! \\ $$$$\boldsymbol{{i}}\:\boldsymbol{{know}}\:\boldsymbol{{also}}\:\boldsymbol{{but}}\:\boldsymbol{{it}}\:\boldsymbol{{is}}\:\boldsymbol{{approximate}} \\ $$$$\boldsymbol{{result}}: \\ $$$$\boldsymbol{{because}} \\ $$$$\boldsymbol{\Gamma}\left(\boldsymbol{{x}}+\mathrm{1}\right)\approx\sqrt{\mathrm{2}\boldsymbol{\pi{x}}}.\boldsymbol{{x}}^{\boldsymbol{{x}}} .\boldsymbol{{e}}^{βˆ’\boldsymbol{{x}}} \\ $$
Commented by mathmax by abdo last updated on 30/Jun/20
x! ∼ (√(2Ο€x))((x/e))^x is approximation of x! at +∞(not equality..!)
$$\mathrm{x}!\:\sim\:\sqrt{\mathrm{2}\pi\mathrm{x}}\left(\frac{\mathrm{x}}{\mathrm{e}}\right)^{\mathrm{x}} \:\mathrm{is}\:\mathrm{approximation}\:\mathrm{of}\:\mathrm{x}!\:\mathrm{at}\:+\infty\left(\mathrm{not}\:\mathrm{equality}..!\right) \\ $$
Commented by Tinku Tara last updated on 30/Jun/20
Some comments in this thread were deleted.
$$\mathrm{Some}\:\mathrm{comments}\:\mathrm{in}\:\mathrm{this}\:\mathrm{thread} \\ $$$$\mathrm{were}\:\mathrm{deleted}. \\ $$
Commented by MJS last updated on 01/Jul/20
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *