d-dx-x-4-2-x-

Question Number 26288 by sakshiraj@gmail.com last updated on 23/Dec/17

$$\frac{\boldsymbol{{d}}}{\boldsymbol{{dx}}}\:\frac{\boldsymbol{{x}}−\mathrm{4}}{\mathrm{2}\sqrt{\boldsymbol{{x}}}} \\ $$

Answered by Joel578 last updated on 24/Dec/17

Use quotient rule u = x − 4 → u′ = 1 v = 2(√x) → v′ = (1/( (√x))) (d/dx)(((x − 4)/(2(√x)))) = ((u′. v − v′ . u)/v^2 ) = ((2(√x) − (1/( (√x)))(x − 4))/(4x)) = ((2(√x) − (x/( (√x))) + (4/( (√x))))/(4x)) = ((x + 4)/(4x(√x))) = (((x + 4)(√x))/(4x^2 ))

$$\mathrm{Use}\:\mathrm{quotient}\:\mathrm{rule} \\ $$$${u}\:=\:{x}\:−\:\mathrm{4}\:\:\rightarrow\:\:{u}'\:=\:\mathrm{1} \\ $$$${v}\:=\:\mathrm{2}\sqrt{{x}}\:\:\:\:\:\:\rightarrow\:\:{v}'\:=\:\frac{\mathrm{1}}{\:\sqrt{{x}}} \\ $$$$ \\ $$$$\frac{{d}}{{dx}}\left(\frac{{x}\:−\:\mathrm{4}}{\mathrm{2}\sqrt{{x}}}\right)\:=\:\frac{{u}'.\:{v}\:−\:{v}'\:.\:{u}}{{v}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2}\sqrt{{x}}\:−\:\frac{\mathrm{1}}{\:\sqrt{{x}}}\left({x}\:−\:\mathrm{4}\right)}{\mathrm{4}{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2}\sqrt{{x}}\:−\:\frac{{x}}{\:\sqrt{{x}}}\:+\:\frac{\mathrm{4}}{\:\sqrt{{x}}}}{\mathrm{4}{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{x}\:+\:\mathrm{4}}{\mathrm{4}{x}\sqrt{{x}}}\:=\:\frac{\left({x}\:+\:\mathrm{4}\right)\sqrt{{x}}}{\mathrm{4}{x}^{\mathrm{2}} } \\ $$

Answered by Rasheed.Sindhi last updated on 27/Dec/17

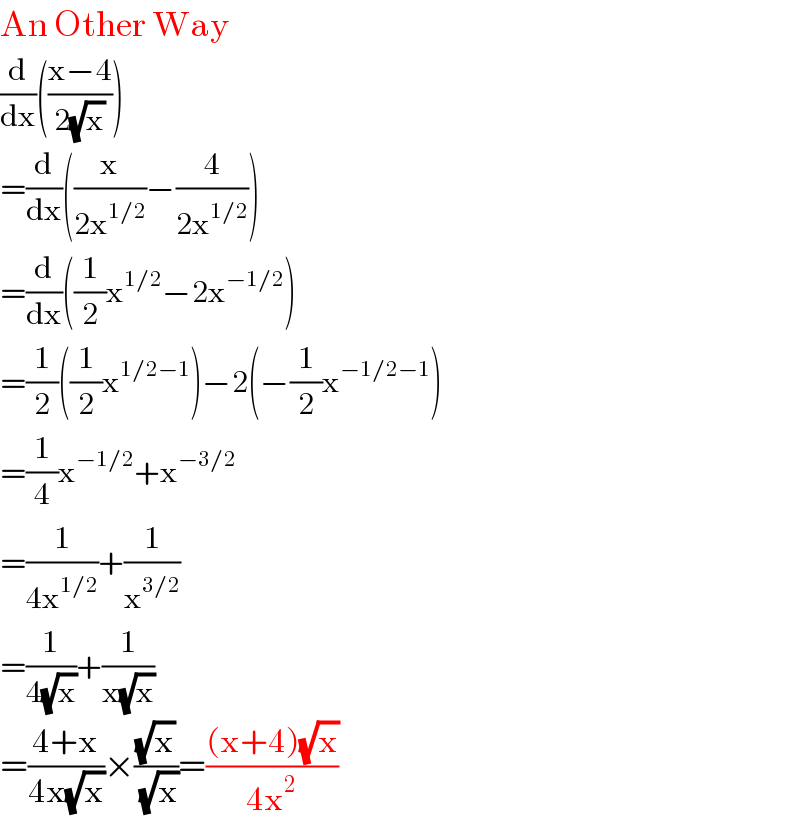
An Other Way (d/dx)(((x−4)/(2(√x)))) =(d/dx)((x/(2x^(1/2) ))−(4/(2x^(1/2) ))) =(d/dx)((1/2)x^(1/2) −2x^(−1/2) ) =(1/2)((1/2)x^(1/2−1) )−2(−(1/2)x^(−1/2−1) ) =(1/4)x^(−1/2) +x^(−3/2) =(1/(4x^(1/2) ))+(1/x^(3/2) ) =(1/(4(√x)))+(1/(x(√x))) =((4+x)/(4x(√x)))×((√x)/( (√x)))=(((x+4)(√x))/(4x^2 ))

$$\mathrm{An}\:\mathrm{Other}\:\mathrm{Way} \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{x}−\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{x}}}\right) \\ $$$$=\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{x}}{\mathrm{2x}^{\mathrm{1}/\mathrm{2}} }−\frac{\mathrm{4}}{\mathrm{2x}^{\mathrm{1}/\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{1}/\mathrm{2}} −\mathrm{2x}^{−\mathrm{1}/\mathrm{2}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{1}/\mathrm{2}−\mathrm{1}} \right)−\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{−\mathrm{1}/\mathrm{2}−\mathrm{1}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}^{−\mathrm{1}/\mathrm{2}} +\mathrm{x}^{−\mathrm{3}/\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4x}^{\mathrm{1}/\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}/\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{x}}}+\frac{\mathrm{1}}{\mathrm{x}\sqrt{\mathrm{x}}} \\ $$$$=\frac{\mathrm{4}+\mathrm{x}}{\mathrm{4x}\sqrt{\mathrm{x}}}×\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{x}}}=\frac{\left(\mathrm{x}+\mathrm{4}\right)\sqrt{\mathrm{x}}}{\mathrm{4x}^{\mathrm{2}} } \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply