Question Number 81226 by 20092104 last updated on 10/Feb/20
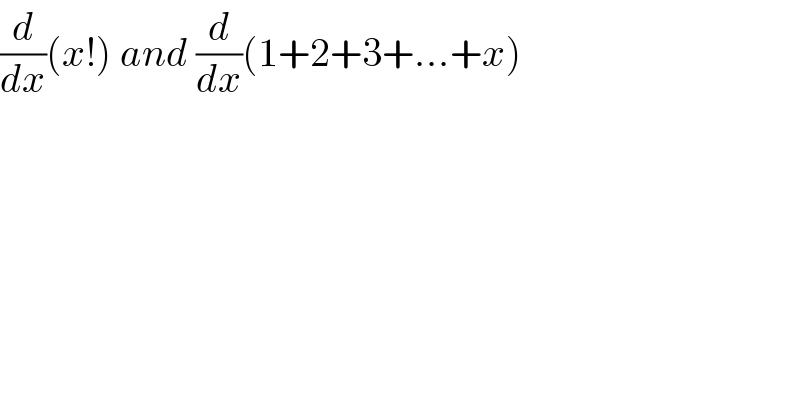
$$\frac{{d}}{{dx}}\left({x}!\right)\:{and}\:\frac{{d}}{{dx}}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{x}\right) \\ $$
Answered by MJS last updated on 10/Feb/20
![(d/dx)[x!] doesn′t exist because x! is not continuous 1+2+3+...+x=((x(x+1))/2) (d/dx)[((x(x+1))/2)]=x+(1/2)](https://www.tinkutara.com/question/Q81232.png)
$$\frac{{d}}{{dx}}\left[{x}!\right]\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}\:\mathrm{because}\:{x}!\:\mathrm{is}\:\mathrm{not}\:\mathrm{continuous} \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{x}=\frac{{x}\left({x}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\frac{{d}}{{dx}}\left[\frac{{x}\left({x}+\mathrm{1}\right)}{\mathrm{2}}\right]={x}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$
