Question Number 172944 by flor last updated on 03/Jul/22
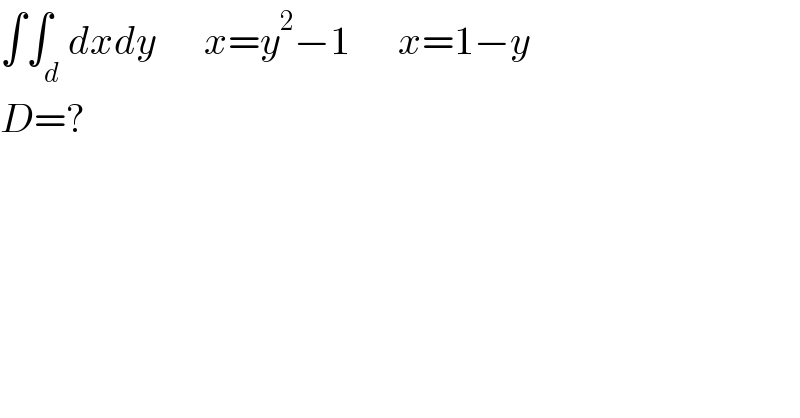
$$\int\int_{{d}} {dxdy}\:\:\:\:\:\:{x}={y}^{\mathrm{2}} −\mathrm{1}\:\:\:\:\:\:{x}=\mathrm{1}−{y} \\ $$$${D}=? \\ $$
Commented by kaivan.ahmadi last updated on 04/Jul/22
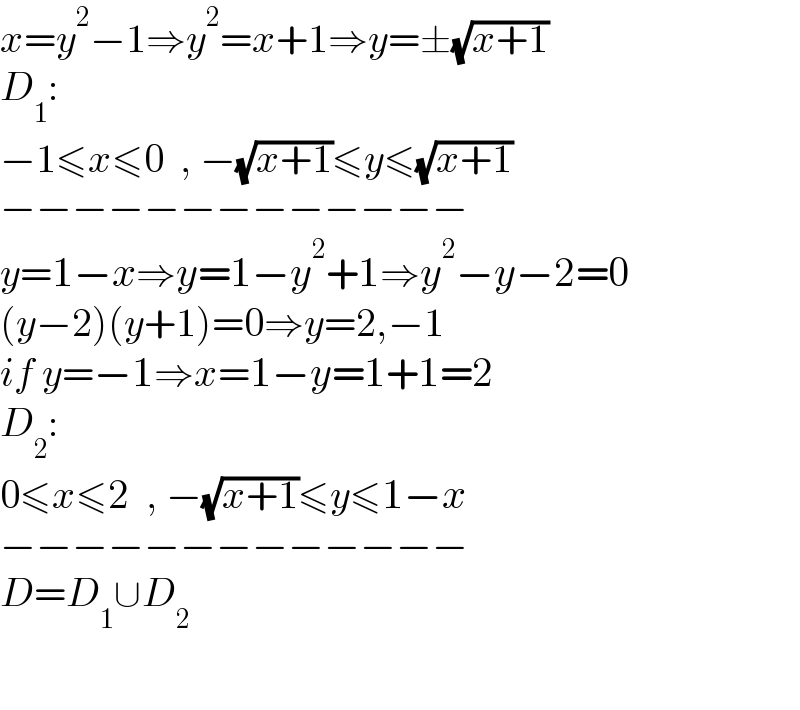
$${x}={y}^{\mathrm{2}} −\mathrm{1}\Rightarrow{y}^{\mathrm{2}} ={x}+\mathrm{1}\Rightarrow{y}=\pm\sqrt{{x}+\mathrm{1}} \\ $$$${D}_{\mathrm{1}} : \\ $$$$−\mathrm{1}\leqslant{x}\leqslant\mathrm{0}\:\:,\:−\sqrt{{x}+\mathrm{1}}\leqslant{y}\leqslant\sqrt{{x}+\mathrm{1}} \\ $$$$−−−−−−−−−−−−− \\ $$$${y}=\mathrm{1}−{x}\Rightarrow{y}=\mathrm{1}−{y}^{\mathrm{2}} +\mathrm{1}\Rightarrow{y}^{\mathrm{2}} −{y}−\mathrm{2}=\mathrm{0} \\ $$$$\left({y}−\mathrm{2}\right)\left({y}+\mathrm{1}\right)=\mathrm{0}\Rightarrow{y}=\mathrm{2},−\mathrm{1} \\ $$$${if}\:{y}=−\mathrm{1}\Rightarrow{x}=\mathrm{1}−{y}=\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$$${D}_{\mathrm{2}} : \\ $$$$\mathrm{0}\leqslant{x}\leqslant\mathrm{2}\:\:,\:−\sqrt{{x}+\mathrm{1}}\leqslant{y}\leqslant\mathrm{1}−{x} \\ $$$$−−−−−−−−−−−−− \\ $$$${D}={D}_{\mathrm{1}} \cup{D}_{\mathrm{2}} \\ $$$$ \\ $$
Answered by kaivan.ahmadi last updated on 04/Jul/22

Commented by kaivan.ahmadi last updated on 04/Jul/22

$${red}\:{line}:\:{y}=\mathrm{1}−{x} \\ $$
Commented by CElcedricjunior last updated on 05/Jul/22
![A=∫_(−1) ^1 ∫_(y−1) ^(y^2 −1) dxdy =∫_(−1) ^1 [x]_(y−1) ^(y^2 −1) dy =∫_(−1) ^1 (y^2 −y)dy =[(y^3 /3)+(y^2 /2)+2y]_(−1) ^1 =(2/3) A=(2/3) .........Le ce^� le^� bre cedric junior.........](https://www.tinkutara.com/question/Q173039.png)
$$\boldsymbol{{A}}=\int_{−\mathrm{1}} ^{\mathrm{1}} \int_{\boldsymbol{{y}}−\mathrm{1}} ^{\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{1}} \boldsymbol{\mathrm{dxdy}} \\ $$$$\:\:\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \left[\boldsymbol{\mathrm{x}}\right]_{\boldsymbol{\mathrm{y}}−\mathrm{1}} ^{{y}^{\mathrm{2}} −\mathrm{1}} \boldsymbol{\mathrm{dy}} \\ $$$$\:\:\:=\int_{−\mathrm{1}} ^{\mathrm{1}} \left(\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\boldsymbol{\mathrm{y}}\right)\boldsymbol{\mathrm{dy}} \\ $$$$\:\:\:=\left[\frac{\boldsymbol{\mathrm{y}}^{\mathrm{3}} }{\mathrm{3}}+\frac{\boldsymbol{\mathrm{y}}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\boldsymbol{\mathrm{y}}\right]_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$$\:\:\:=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathscr{A}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$………\mathscr{L}{e}\:{c}\acute {{e}l}\grave {{e}bre}\:{cedric}\:{junior}……… \\ $$$$ \\ $$
